Экономико-математическая модель транспортной задачи

Одной из типичных задач линейного программирования является так называемая транспортная задача. Она возникает при планировании наиболее рациональных перевозок грузов, а также при организации и планировании производства.

Любую задачу линейного программирования можно решить симплекс-методом. Однако, существуют методы, которые учитывают конкретные особенности решаемой задачи, а потому более эффективные. Для транспортной задачи – это метод потенциалов.

Транспортная задача в общем виде формулируется следующим образом.

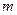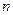Пусть имеется пунктов отправления грузов (или пунктов производства продукции) и пунктов назначения груза (или пунктов потребления продукции) .

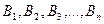Обозначим запасы груза (или ресурсы производства) в 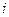- ом пункте отправления через 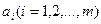, т.е 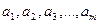, а потребность каждого 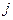- ого пункта потребления через 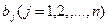, т.е .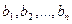

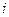Заданы стоимости перевозки единицы груза от каждого - ого пункта отправления до каждого 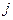- ого пункта потребления.

Требуется определить, какое количество груза 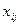необходимо перевезти из каждого 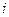-ого пункта отправления до каждого 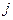- ого пункта потребления так, чтобы:

- вывести грузы всех поставщиков;

- удовлетворить всех потребителей;

- достичь минимального значения общей стоимости перевозок.

Чтобы лучше представить условие задачи, сведем все исходные данные в таблицу 1.2 называемую матрицей планирования перевозок.

Строки таблицы соответствуют поставщикам, а столбцы потребителям. В последней строке записаны заявки каждого потребителя, а в последнем столбце запасы каждого поставщика. В верхних правых углах внутренних клеток таблицы записываются истинные тарифы , а в нижних левых – планируемые перевозки .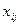

Таблица 2.

поставщики	потребители	запасы
		…		…
			…		…
			…		…
…	…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…	…
			…		…
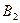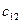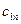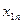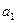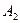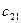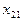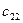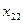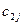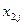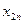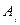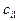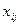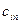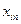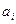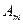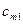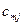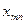потребности			…		…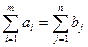

Какие соотношения могут быть между запасами и потребностями?

При постановке задач перевозки грузов могут возникнуть три различные ситуации:

1. количество груза у всех поставщиков равно потребностям всех потребителей в данном грузе:

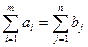; (18)

2. количество груза у всех поставщиков больше заказов всех потребителей на данный груз:

; (19)

3. количество груза у всех поставщиков меньше потребностей всех потребителей в данном грузе:

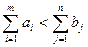. (20)

При выполнении условия (18), накладываемого на соотношение запасов груза и потребностей в нем, т.е. при равенстве общих запасов и общих потребностей, экономико-математическая модель транспортной задачи называется закрытой, а сама задача – сбалансированной.

Модели, для которых запасы не равны потребностям, т.е. выполняются соотношения (19) или (20), называются – открытыми, а задачи - несбалансированными.

Рассмотрим, какие ограничения следует наложить на неизвестные 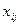для сбалансированной задачи. Из соотношения (5.18) следует, что весь груз, имеющейся у поставщиков, должен быть вывезен, и каждый потребитель должен получить столько груза, сколько ему необходимо, поэтому

Первая группа ограничений означает, что весь груз, имеющейся у каждого из поставщиков, должен быть вывезен (количество ограничений равно числу поставщиков - ):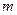

(21)

Вторая группа ограничений означает, что каждый потребитель должен получить ровно столько груза, сколько ему необходимо (количество ограничений равно числу потребителей - ):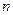

(22)

Третья группа ограничений означает, что количество перевозимого груза должно быть величиной неотрицательной:

(23)

Как записать целевую функцию транспортной задачи?

Цель решения задачи – составить план перевозок грузов, обеспечивающий минимальные транспортные расходы. Следовательно, критерием задачи являются минимальные транспортные расходы.

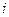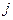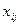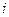Стоимость перевозки единицы груза от - ого пункта отправления до - ого пункта потребления составляет . Стоимость перевозки всего груза от - ого пункта отправления до 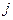- ого пункта потребления составляет .

Суммарная стоимость перевозки единицы груза от всех поставщиков ко всем потребителям должна быть минимальной и будет равна:

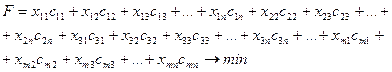(24)

Математическая модель транспортной задачи в компактной форме имеет вид:

(25)

Разрешимой является только закрытая модель или сбалансированная транспортная задача, т.е. для существования оптимального плана необходимо и достаточно, чтобы выполнялось условие (5.18). Чтобы решить открытую транспортную задачу, ее необходимо сбалансировать, т.е. свести к закрытой.

Для сведения открытой транспортной задачи к закрытой необходимо:

1. В случае, когда запасы в пунктах отправления превосходят потребности всех пунктов назначения, т.е. выполнено условие (5.19)

, необходимо ввести фиктивного потребителя (пункт назначения) 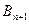с потребностью в грузе равной разности общих запасов и общих потребностей: .

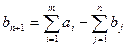Так как введенный потребитель фиктивный, то все истинные тарифы доставки груза полагают равными нулю .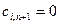

В реальности излишки груза останутся в пунктах отправления и с введением фиктивного потребителя такая открытая задача станет разрешимой.

В этом случае в матрицу планирования перевозок добавится еще один столбец, соответствующий фиктивному потребителю 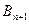(таблица 3).

Экономико-математическая модель в этом случае выглядит следующим образом:

Таблица 3.

поставщики	потребители	запасы
		…		…
			…		…
			…		…
…	…	…	…	…	…	…		…
			…		…
…	…	…	…	…	…	…		…
			…		…
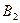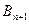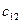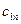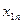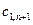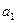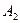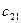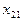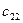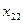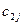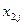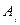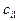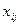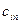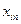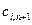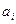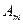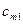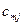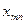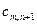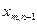потребности			…		…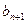

В случае, когда запасы в пунктах отправления меньше потребности всех пунктов назначения, т.е. выполнено условие (20)

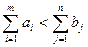, необходимо ввести фиктивного поставщика (пункт отправления) 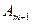с наличием груза в количестве, равном разности общих потребностей и общих запасов: .

Так как введенный поставщик фиктивный, то все истинные тарифы доставки груза из этого пункта полагают равными нулю .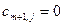

В реальности нехватка груза распределится по всем пунктам назначения и с введением фиктивного поставщика открытая задача станет разрешимой.

В этом случае в матрицу планирования перевозок добавится еще одна строка, соответствующая фиктивному поставщику 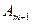(таблица 5.4).

Экономико-математическая модель в этом случае выглядит следующим образом:

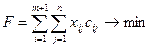
Таблица 4.

поставщики	потребители	запасы
	…		…
		…		…
		…		…
…	…	…	…	…	…	…
		…		…
…	…	…	…	…	…	…
		…		…
		…		…
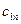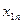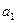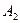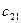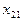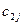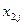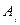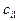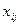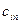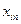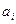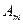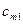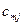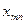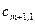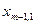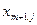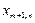потребности		…		…

8. Модели и методы сетевого планирования и управления (СПУ)

СПУ основано на моделировании с помощью сетевого графика и представляет собой совокупность расчетных методов, организационных и контрольных мероприятий по планированию и управлению комплексом работ.

Система СПУ позволяет:

- формировать календарный план реализации некоторого комплекса работ;

- выявлять и мобилизовать резервы времени, трудовые материальные и денежные ресурсы;

- осуществлять управление комплексом работ по принципу «ведущего звена» с прогнозированием и предупреждением возможных срывов в ходе работы;

- повышать эффективность управления в целом при четком распределении ответственности между руководителями разных уровней и исполнителями работ.

Под комплексом работ (комплексом операций, или проектом) будем понимать всякую задачу, для выполнения которых необходимо осуществить достаточно большое количество разнообразных работ.