Модель Леонтьева многоотраслевой экономики

Эффективное введение народного хозяйства предполагает наличие баланса между отдельными отраслями. Каждая отрасль при этом выступает двояко: с одной стороны, как производитель некоторой продукции, а с другой – как потребитель продуктов, вырабатываемых другими отраслями. Для наглядного выражения взаимной связи между отраслями пользуются определенного вида таблицами, называемыми таблицами межотраслевого баланса. В общем виде таблица имеет вид:

ресурсы	распределение
№ п/п	источники	объем	№ п/п	потребности	объем
	производство		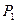	Производственно-эксплуатационные нужды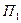
	импорт			Капитальное строительство
	остатки на начало года и прочие источники		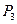	экспорт
				Рыночные фонды
				Остатки на конец года и прочие нужды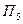

Условие сбалансированности между производством и потребностями требует выполнения равенства

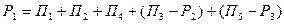
т.е. объем производства должен быть равен алгебраической сумме указанных в таблице показателей.

Более современная развитая математическая модель межотраслевого баланса, допускающая широкие возможности анализа появились в 1936 г. в трудах американского экономиста В. Леонтьева. Далее рассматривается наиболее простой вариант такой модели, сохраняющей, однако, ее основное математическое содержание.

Предположим, что вся производящая сфера народного хозяйства разбита на некоторое число n отраслей, каждая из которых производит свой однородный продукт, причем разные отрасли производят разные продукты. Разумеется, такое представление об отрасли является в значительной мере абстракцией, т.к. в реальной экономике отрасль определяется не только названием выпускаемого продукта, но и ведомственной принадлежностью своих предприятий (например, данному министерству, тресту и т.п.). Однако представление отрасли в указанном смысле позволяет «в первом приближении» провести анализ структуры народного хозяйства.

Итак, предполагаем, что имеется n различных отраслей О₁, О₂,…, О_i, каждая из которых производит свой продукт. В дальнейшем отрасль О_i будем называть «i-тая отрасль». В процессе производства своего продукта каждая отрасль нуждается в продукции других отраслей (производственное потребление). Будем вести речь о некотором определенном промежутке времени [T₀,T₁] (обычно плановый год) и введем следующие обозначения:

x_i – общий объем продукции отрасли за данный промежуток времени – так называемый валовой выпуск отрасли;

x_ij – объем продукции отрасли i, расходуемый отраслью j в процессе производства;

y_i – объем продукции отрасли i, предназначенный к потреблению в непроизводственной сфере – объем конечного потребления. Этот объем составляет обычно более 75% всей произведенной продукции. В него входят создаваемые в хозяйстве запасы, личное потребление граждан, обеспечение общественных потребностей (просвещение, наука, здравоохранение, развитие инфраструктуры и т.д.), поставки на экспорт.

Указанные величины можно свести в таблицу:

Производственное потребление	Конечное потребление	Валовой выпуск
x11 x12 … x1n	y1	x1
x21 x22 … x2n	y2	x2
……………………	…	…
xn1 xn2 … xnn	yn	xn

Балансовый характер этой таблицы выражается в том, что при любом i=1,…, и должно выполняться соотношение

(1)

означающее, что валовой выпуск x_i расходуется на производственное потребление, равное , и непроизводственное потребление, равное y_i.

Единицы измерения всех указанных величин могут быть или натуральными (кубометры, тонны, штуки, киловатт-часы и т.п.) или стоимостными. В зависимости от этого различают натуральный и стоимостный межотраслевой баланс. Для определенности в дальнейшем будем иметь в виду стоимостный баланс.

В. Леонтьев, рассматривая развитие американской экономики в предвоенный период, обратил внимание на следующее обстоятельство: а именно, величины

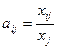
остаются постоянными в течение ряда лет. Это обуславливается примерным постоянством используемой технологии.

Исходя из этого сделаем такое допущение: для выпуска любого объема x_j продукции отрасли j необходимо затратить продукцию отрасли 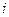в количестве a_ijx_j, где a_ij – постоянный коэффициент. Проще говоря, материальные издержки пропорциональны объему производимой продукции. Принцип линейности распространяется и на другие виды издержек, например, на оплату труда, нормативную прибыль.

Итак, согласно гипотезе линейности имеем:

(2)

Коэффициенты a_ij называют коэффициентами прямых затрат.

В предположении линейности соотношения (6.1) принимают вид:

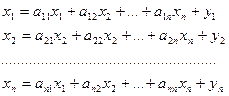
или в матричной записи

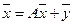(3)

где

, ,

Вектор 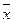называется вектором валового выпуска, вектор – вектором конечного потребления,а матрица А – матрицей прямых затрат. Соотношение (6.3) называется уравнением линейного межотраслевого баланса. Вместе с изложенной интерпретацией матрицы А и векторов 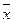и это соотношение называется также моделью Леонтьева.

Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска 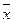, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта . При этом нужно иметь в виду следующие особенности системы (6.3):

- все компоненты матрицы А и вектора неотрицательны (это вытекает из экономического смысла А и );

- все компоненты вектора 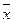также должны быть неотрицательными.

Перепишем уравнение (6.3) в виде:

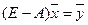(4)

где Е – единичная матрица.

Если матрица невырожденная, т.е. , то решением системы (6.3) методом обратной матрицы будет матрица-столбец

(5)

Матрица называется матрицей полных затрат.

Выясним экономический смысл элементов матрицы S=(s_ij). Для этого зададим единичные вектора конечного продукта

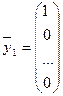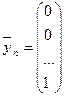, ,…, , тогда в соответствии с (6.5) соответствующие векторы валового выпуска будут

, ,…, .

Следовательно, каждый элемент матрицы 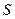есть величина валового выпуска продукции 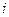- той отрасли, необходимого для обеспечения выпуска единицы конечного продукта 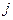- той отрасли .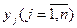