Информационная безопасность и защита информации

Информационная безопасность и защита информации

Билет

1. Генерация последовательностей ПСЧ. Параметры генератора.

ГПСЧ не являются истинно случайными, поскольку генерируют последовательность чисел по некоторому алгоритму.

Основные характеристики алгоритма псевдослучайной генерации: начальное значение и период.

Начальное значение требуется по той причине, что обычно следующие числа зависят от предыдущих (рекуррентные соотношения). Вспомните: в любом адекватном рекуррентном соотношении есть некое граничное условие, например, если факториал представлять как n! = n * (n-1)!, то 0! = 1 - граничное условие. Другое пример - числа Фибоначчи: f(0) = f(1) = 1 - граничное условие, f(n) = f(n - 1) + f(n - 2) - рекуррентное соотношение. Каждый запросто может придумать другие - самопальные - рекуррентные соотношения...

Период - наименьшее T такое, что гарантированно X(i) = X(i + T), где i - целое неотрицательное (ведём нумерацию элементов последовательности с нуля), X(i) - i-ый член последовательности. Иначе говоря, псевдослучайная последовательность представляет собой серию повторяющихся групп из T чисел. Например, {2, 3, 0, 1, 2, 3, 0, 1, 2, ...} - здесь период T = 4, начальное значение X(0) = 2.

Зная алгоритм ГПСЧ и начальное значение, легко восстановить любое число X(i).

А теперь сформулируем требования, по которым в криптографии создаются ГПСЧ:

1. Псевдослучайная последовательность, выдаваемая ГПСЧ, должна иметь как можно больший период. Чем секретнее данные, тем больший период желательно иметь.
2. Зная любой фрагмент последовательности, выдаваемой генератором, злоумышленник не должен иметь эффективной возможности найти начальное значение, загруженное в генератор.
3. Зная любой фрагмент последовательности, выдаваемой генератором, злоумышленник не должен иметь возможности получить достоверную информацию о предыдущих или последующих элементах последовательности.
4. Ну и, разумеется, хотелось бы повыше скорость работы генератора. К сожалению, это несколько противоречит тому, что требуется как можно более высокая защищённость.

Требования 2 и 3 можно считать требованиями непредсказуемости.

Существуют истинно случайные генераторы. Примером такого может быть, например, игральный куб без смещённого центра тяжести и прочих жульнических штучек. Но в криптографии принято использовать ГПСЧ, поэтому их касаться не будем.

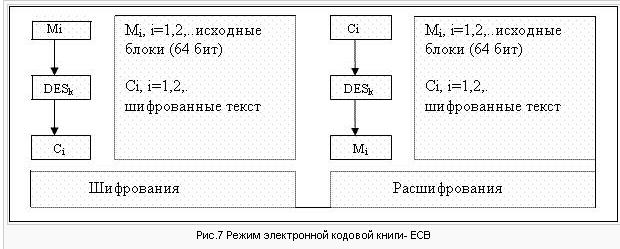
2. DES стандарт. Режим электронной кодовой книги.

Стандарт шифрования данных (DES)— блочный шифр с симметричными ключами, разработан Национальным Институтом Стандартов и Технологии (NIST – National Institute of Standards and Technology).

DES (Data Encryption Standart) — Симметричный алгоритм шифрования, в котором один ключ используется, как для шифрования, так и для расшифрования данных. DES разработан фирмой IBM и утвержден правительством США в 1977 году как официальный стандарт (FTPS 46-3). DES имеет блоки по 64 бит и 16 цикловую структуру сети Фейстеля, для шифрования использует ключ с длиной 56 бит. Алгоритм использует комбинацию нелинейных (S-блоки) и линейных (перестановки E, IP, IP-1) преобразований. Для DES рекомендовано несколько режимов:

· режим электронной кодовой книги (ECB — Electronic Code Book),

· режим сцепления блоков (СВС — Cipher Block Chaining),

· режим обратной связи по шифротексту (CFB — Cipher Feed Back),

· режим обратной связи по выходу (OFB — Output Feed Back).

Билет

1. Традиционные методы шифрования. Шифры перестановки

Шифры перестановки. При шифровании перестановкой символы шифруемого текста переставляются по определенному правилу в пределах блока этого текста. Шифры перестановки являются самыми простыми и, вероятно, самыми древними шифрами.

Простая перестановка без ключа (с ключом рассматривается здесь) — один из самых простых методов шифрования.

Делают так:

1. Сообщение записывается в таблицу по столбцам.
2. После того, как открытый текст записан колонками, для образования шифровки он считывается по строкам. Для использования этого шифра отправителю и получателю нужно договориться об общем ключе в виде размера таблицы.

например, зашифруем фразу "ВРАГ БУДЕТ РАЗБИТ",
разместим текст в "таблице" - по три столбца (и не будем вообще использовать пробелы)-
запишем текст столбцами:

?

В Г Д Р Б   Р Б Е А И   А У Т З Т

при считывании по строкам получим шифровку (разделяю на группы по 4-ре только для визуального удобства - можно вообще не разделять):

?

ВГДР БРБЕ АИАУ ТЗТ

То есть мы получаем перестановку (как результат действия подстановки) исходного множества букв (потому так и называется) таким образом:

?

ВРАГ БУДЕ ТРАЗ БИТ ВГДР БРБЕ АИАУ ТЗТ

Фактически - чтобы сразу расшифровать такую строку:

?

ВРАГ БУДЕ ТРАЗ БИТ

достаточно знать число столбцов в исходной таблице,то есть число столбцов и будет являться ключом данной криптосистемы.

Но, как вы поняли на компьютере такая защита весьма просто ломается путём подбора числа столбцов (проверка - получение связного текста)

1. AES стандарт. RIJNDAEL. Структура.

Алгоритм шифрования, действующий в качестве государственного стандарта в области шифрования данных в США с 2001 года. В основу стандарта положен шифр Rijndael. Шифр Rijndael/AES (то есть рекомендуемый стандартом) характеризуется размером блока 128 бит, длиной ключа 128, 192 или 256 бит и количеством раундов 10, 12 или 14 в зависимости от длины ключа. Основу Rijndael составляют так называемые линейно-подстановочные преобразования. В алгоритме широко используются табличные вычисления, причем все необходимые таблицы задаются константно, т.е. не зависят ни от ключа, ни от данных.

Данный алгоритм разработан двумя специалистами по криптографии из Бельгии. Он является нетрадиционным блочным шифром, поскольку не использует сеть Фейштеля для криптопреобразований. Алгоритм представляет каждый блок кодируемых данных в виде двумерного массива байт размером 4х4, 4х6 или 4х8 в зависимости от установленной длины блока. Далее на соответствующих этапах преобразования производятся либо над независимыми столбцами, либо над независимыми строками, либо вообще над отдельными байтами в таблице.

Все преобразования в шифре имеют строгое математическое обоснование. Сама структура и последовательность операций позволяют выполнять данный алгоритм эффективно как на 8-битных так и на 32-битных процессорах. В структуре алгоритма заложена возможность параллельного исполнения некоторых операций, что на многопроцессорных рабочих станциях может еще поднять скорость шифрования в 4 раза.

Алгоритм состоит из некоторого количества раундов (от 10 до 14 – это зависит от размера блока и длины ключа), в которых последовательно выполняются следующие операции :

• ByteSub – табличная подстановка 8х8 бит (рис.6),

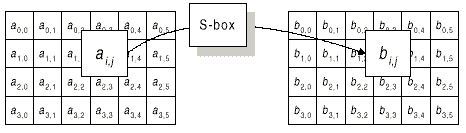
Рис.6.

• ShiftRow – сдвиг строк в двумерном массиве на различные смещения (рис.7),

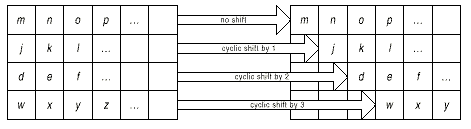
Рис.7.

• MixColumn – математическое преобразование, перемешивающее данные внутри столбца (рис.8),

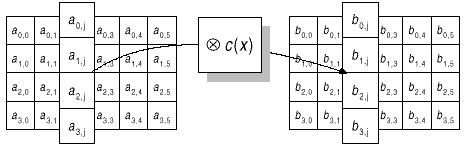
Рис.8.

• AddRoundKey – добавление материала ключа операцией XOR (рис.9).

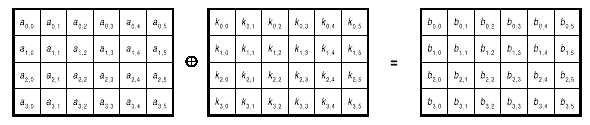
Рис.9.

В последнем раунде операция перемешивания столбцов отсутствует, что делает всю последовательность операций симметричной.

1. ГОСТ 28147-89. Режим простой замены.

2.1. Зашифрование открытых данных в режиме простой замены

2.1.1. Криптосхема, реализующая алгоритм зашифрования в режиме простой замены, должна иметь вид, указанный на черт.2.

Билет

1. ГОСТ 28147-89. Режим гаммирования с обратной связью.

Алгоритм RSA

Следующий пример наглядно демонстрирует алгоритм шифрования RSA:

Зашифруем и расшифруем сообщение "САВ" по алгоритму RSA. Для простоты возьмем небольшие числа - это сократит наши расчеты.

• Выберем p=3 and q=11.
• Определим n= 3*11=33.
• Hайдем (p-1)*(q-1)=20. Следовательно, d будет равно, например, 3: (d=3).
• Выберем число е по следующей формуле: (e*3) mod 20=1. Значит е будет равно, например, 7: (e=7).
• Представим шифруемое сообщение как последовательность чисел в диапозоне от 0 до 32 (незабывайте, что кончается на n-1). Буква А =1, В=2, С=3.

Теперь зашифруем сообщение, используя открытый ключ {7,33}

C1 = (3^7) mod 33 = 2187 mod 33 = 9;
C2 = (1^7) mod 33 = 1 mod 33 = 1;
C3 = (2^7) mod 33 = 128 mod 33 = 29;

Теперь расшифруем данные, используя закрытый ключ {3,33}.

M1=(9^3) mod 33 =729 mod 33 = 3(С);
M2=(1^3) mod 33 =1 mod 33 = 1(А);
M3=(29^3) mod 33 = 24389 mod 33 = 2(В);

Данные расшифрованы!

Билет

Билет

Пример 12.35

Следующий пример содержит систему уравнений с различными модулями:

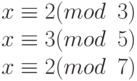
Для этой системы уравнений x = 23. Это значение удовлетворяет все уравнения: , , .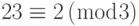

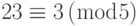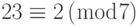Решение

Решение системы уравнений выполняется в следующем порядке:

1. Найти . Это общий модуль.
2. Найти M₁ = M/m₁, M₂ = M/m₂,…., M_k = M/m_k.
3. Используя соответствующие модули m₁, m₂,…., m_k, найти мультипликативную инверсию M₁, M₂,…, M_k. Обозначим ее M₁^-1, M₂^-1,…, M_k^-1.
4. Решение системы уравнений

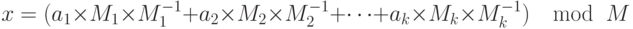
Обратите внимание, что система уравнений может иметь решение, даже если модули не взаимно простые. Однако в криптографии мы интересуемся только решением уравнений с взаимно простыми модулями.

Пример 12.36

Найдите решение системы уравнений

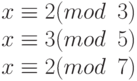
Из предыдущего примера мы уже знаем, что ответ x = 23. Определим его в четыре шага.

Решение

1. 
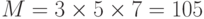
2. M₁ = 105/3 = 35, M₂ = 105/5 =21, M₃ = 105/7 = 15
3. Инверсии M₁^-1 = 2, M₂^-1 = 1, M₃^-1 = 1
4. 

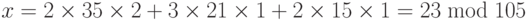
Пример 12.37

Найти целое, которое дает в остатке 3, если его разделить на 7 и 13, но без остатка делится на 12.

Решение

Это проблема китайской теоремы об остатке. Мы можем составить три уравнения и найти значение x.

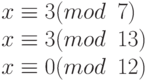
Если проведем четыре шага, мы найдем x = 276. Можем проверить, что 276 = 3 mod 7, 276 = 3 mod 13 и 276 делится на 12 (частное 23 и остаток 0).

Приложения

Китайская теорема об остатках часто применяется в криптографии. Одно из таких применений – решение квадратных уравнений — будет обсуждаться в следующей секции. Другое приложение — представление очень большого числа в виде списка малых целых чисел.

Пример 12.38

Предположим, нам надо вычислить z = x + y, где x = 123 и y = 334, но система принимает только числа меньше 100. Эти числа можно представить следующими уравнениями:

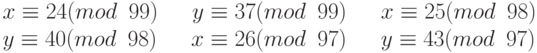
Сложим каждое уравнение x с соответствующим уравнением y:

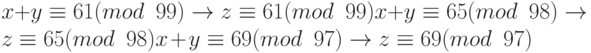
Теперь эти три уравнения могут быть решены, используя китайскую теорему об остатках, чтобы найти z. Один из приемлемых ответов равен z = 457.

Квадратичные вычеты.

В уравнении 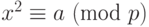. a называется квадратичным вычетом (QR), если уравнение имеет два решения; a называется квадратичным невычетом (QNR), если уравнение не имеет решений. Может быть доказано, что в Z_P* с p – 1 элементами (p – 1)/2 элементов — квадратичные вычеты и (p – 1)/2 являются квадратичными невычетами.

Пример 13.3

Есть 10 элементов в Z_11*. Пять из них – квадратичные вычеты, и пять — невычеты. Другими словами, Z_11* может быть разделен на два отдельных множества, QR и QNR, как это показано на рис. 13.1.

Вычисления в конечных полях

В конечных полях, как обычно, можно складывать, вычитать, умножать и делить.

Задача 2.65. Решить следующую систему уравнений над :

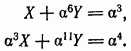
(Следует воспользоваться таблицей соответствия из задачи 2.59.)

Решение. Используем метод подстановки. Из первого уравнения находим подставляя его во второе уравнение, получаем

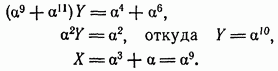
Для решения указанной выше системы уравнений можно воспользоваться также методом Крамера:

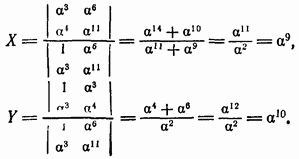
Утверждение 2.66. Пусть 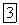— произвольный ненулевой элемент поля Если существует такой элемент 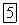что то а называется квадратичным вычетом.

В противном случае, т. е. если в не существует такого элемента что называется квадратичным невычетом.

1) Если то любой элемент поля, за исключением элемента 0, является квадратичным вычетом.

2) Если нечетное число, то четные степени примитивного элемента являются квадратичными вычетами, а нечетные степени — квадратичными невычетами (следовательно, имеется квадратичных вычетов и столько же квадратичных невычетов).

Билет

Билет

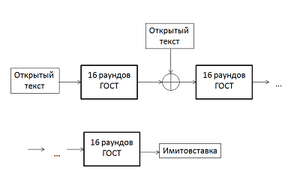
1. ГОСТ 28147-89. Режим выработки имитовставки.

Этот режим не является в общепринятом смысле режимом шифрования. При работе в режиме выработки имитовставки создаётся некоторый дополнительный блок, зависящий от всего текста и ключевых данных. Данный блок используется для проверки того, что в шифротекст случайно или преднамеренно не были внесены искажения. Это особенно важно для шифрования в режиме гаммирования, где злоумышленник может изменить конкретные биты, даже не зная ключа; однако и при работе в других режимах вероятные искажения нельзя обнаружить, если в передаваемых данных нет избыточной информации.

Имитовставка вырабатывается для M ≥ 2 блоков открытого текста по 64 бит. Алгоритм следующий:

1. Блок открытых данных записывается в регистры N₁ и N₂, после чего подвергается преобразованию, соответствующему первым 16 циклам шифрования в режиме простой замены
2. К полученному результату побитно по модулю 2 прибавляется следующий блок открытых данных. Последний блок при необходимости дополняется нулями. Сумма также шифруется в соответствии с пунктом 1.
3. После добавления и шифрования последнего блока из результата выбирается имитовставка длиной L бит: с бита номер 32-L до 32 (отсчёт начинается с 1). Стандарт рекомендует выбирать L исходя из того, что вероятность навязывания ложных данных равна 2^-L. Имитовставка передается по каналу связи после зашифрованных блоков.

Для проверки принимающая сторона после расшифровывания текста проводит аналогичную описанной процедуру. В случае несовпадения результата с переданной имитовставкой все соответствующие M блоков считаются ложными.

Следует отметить, что выработка имитовставки может проводиться параллельно шифрованию с использованием одного из описанных выше режимов работы

2. Алгоритм Диффи-Хеллмана

Предположим, что обоим абонентам известны некоторые два числа g и p, которые не являются секретными и могут быть известны также другим заинтересованным лицам. Для того, чтобы создать неизвестный более никому секретный ключ, оба абонента генерируют большие случайные числа: первый абонент — число a, второй абонент — число b. Затем первый абонент вычисляет значение A = g^amod p и пересылает его второму, а второй вычисляет B = g^bmod p и передаёт первому. Предполагается, что злоумышленник может получить оба этих значения, но не модифицировать их (то есть у него нет возможности вмешаться в процесс передачи). На втором этапе первый абонент на основе имеющегося у него a и полученного по сети B вычисляет значение B^amod p = g^abmod p, а второй абонент на основе имеющегося у него b и полученного по сети A вычисляет значение A^bmod p = g^abmod p. Как нетрудно видеть, у обоих абонентов получилось одно и то же число: K = g^abmod p. Его они и могут использовать в качестве секретного ключа, поскольку здесь злоумышленник встретится с практически неразрешимой (за разумное время) проблемой вычисления g^abmod p по перехваченным g^amod p и g^bmod p, если числа p,a,b выбраны достаточно большими.

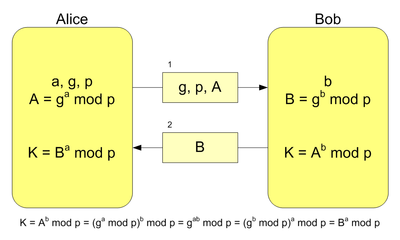
Алгоритм Диффи — Хеллмана, где K — итоговый общий секретный ключ

При работе алгоритма, каждая сторона:

1. генерирует случайное натуральное число a — закрытый ключ
2. совместно с удалённой стороной устанавливает открытые параметры p и g (обычно значения p и g генерируются на одной стороне и передаются другой), где

p является случайным простым числом

g является первообразным корнем по модулю p

1. вычисляет открытый ключ A, используя преобразование над закрытым ключом

A = g^a mod p

1. обменивается открытыми ключами с удалённой стороной
2. вычисляет общий секретный ключ K, используя открытый ключ удаленной стороны B и свой закрытый ключ a

K = B^a mod p

К получается равным с обоих сторон, потому что:

B^a mod p = (g^b mod p)^a mod p = g^ab mod p = (g^a mod p)^b mod p = A^b mod p

В практических реализациях, для a и b используются числа порядка 10¹⁰⁰ и p порядка 10³⁰⁰. Число g не обязано быть большим и обычно имеет значение в пределах первого десятка.

3. Схема шифрования Эль Гамаля.

Асимметричный алгоритм, предложенный в 1985 году Эль-Гамалем (T. ElGamal), универсален. Он может быть использован для решения всех трех основных задач: для шифрования данных, для формирования цифровой подписи и для согласования общего ключа. Кроме того, возможны модификации алгоритма для схем проверки пароля, доказательства идентичности сообщения и другие варианты. Безопасность этого алгоритма, так же как и алгоритма Диффи-Хеллмана, основана на трудности вычисления дискретных логарифмов. Этот алгоритм фактически использует схему Диффи-Хеллмана, чтобы сформировать общий секретный ключ для абонентов, передающих друг другу сообщение, и затем сообщение шифруется путем умножения его на этот ключ.

И в случае шифрования, и в случае формирования цифровой подписи каждому пользователю необходимо сгенерировать пару ключей. Для этого, так же как и в схеме Диффи-Хеллмана, выбираются некоторое большое простое число Р и число А, такие, что различные степени А представляют собой различные числа по модулю Р. Числа Р и А могут передаваться в открытом виде и быть общими для всех абонентов сети.

Затем каждый абонент группы выбирает свое секретное число Х_i, 1 < Х_i < Р-1, и вычисляет соответствующее ему открытое число 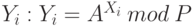. Таким образом, каждый пользователь может сгенерировать закрытый ключ Х_i и открытый ключ Y_i.

Информация о необходимых параметрах системы сведена в следующую таблицу.

	Общие параметры	Открытый ключ	Закрытый ключ
Пользователь 1	Р, А	Y1	Х1
…	…	…
Пользователь i	Yi	Хi

Шифрование

Теперь рассмотрим, каким образом производится шифрование данных. Сообщение, предназначенное для шифрования, должно быть представлено в виде одного числа или набора чисел, каждое из которых меньше Р. Пусть пользователь 1 хочет передать пользователю 2 сообщение m. В этом случае последовательность действий следующая.

1. Первый пользователь выбирает случайное число k, взаимно простое с Р-1, и вычисляет числа

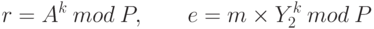
где Y₂ – открытый ключ пользователя 2. Число k держится в секрете.

1. Пара чисел (r, е), являющаяся шифротекстом, передается второму пользователю.
2. Второй пользователь, получив (r,e), для расшифрования сообщения вычисляет

где Х₂ – закрытый ключ пользователя 2. В результате он получает исходное сообщение m.

Если злоумышленник узнает или перехватит Р, А, Y₂, r, e, то он не сможет по ним раскрыть m. Это связано с тем, что противник не знает параметр k, выбранный первым пользователем для шифрования сообщения m. Вычислить каким-либо образом число k практически невозможно, так как это задача дискретного логарифмирования. Следовательно, злоумышленник не может вычислить и значение m, так как m было умножено на неизвестное ему число. Противник также не может воспроизвести действия законного получателя сообщения (второго абонента), так как ему не известен закрытый ключ Х₂ (вычисление Х₂ на основании Y₂ — также задача дискретного логарифмирования).

По аналогичному алгоритму может производиться и согласование ключа, используемого для симметричного шифрования больших объемов данных. Более того, алгоритм Эль-Гамаля на практике целесообразно использовать именно для согласования общего ключа сессии, а не прямого шифрования больших сообщений. Это связано с тем, что в алгоритме используются операции возведения в степень и умножения по большому модулю. Так же как и в алгоритмах RSA и Диффи-Хеллмана, операции производятся над большими, состоящими из нескольких сотен или тысяч бит, числами. Поэтому шифрование больших сообщений производится крайне медленно.

Билет

1. Безопасные хэш-функции. Функции хэширования.

Хэш-функция — это преобразование, получающее из данных произвольной длины некое значение (свертку) фиксированной длины. Простейшими примерами являются контрольные суммы (например, crc32). Бывают криптографические и программистские хэши. Криптографический хэш отличается от программистского следующими двумя свойствами: необратимостью и свободностью от коллизий. Обозначим m – исходные данные, h(m) – хэш от них. Необратимость означает, что если известно число h0, то трудно подобрать m такое, что h(m) = h0. Свободность от коллизий означает, что трудно подобрать такие m1 и m2, что m1 не равно m2, но h(m1) = h(m2).

Криптографические хэш-функции разделяются на два класса:

• хэш-функции без ключа (MDC (Modification (Manipulation) Detect Code) - коды),
• хэш-функции c ключом (MАC (Message Authentication Code) - коды).
• Хэш-функции без ключа разделяются на два подкласса:
• слабые хэш-функции,
• сильные хэш-функции.

Слабой хэш-функцией называется односторонняя функция H(x), удовлетворяющая следующим условиям:

1. аргумент x может быть строкой бит произвольной длины;
2. значение H (x)должно быть строкой бит фиксированной длины;
3. значение H (x)легко вычислить;
4. для любого фиксированного x вычислительно невозможно найти другой x'!=x, такой что H(x')=H(x). Пара x'!=x, когда H(x')=H(x)называется коллизией хэш-функции.

Сильной хэш-функцией называется односторонняя функция H(x), удовлетворяющая условиям 1–3 для слабой хэш-функции и свойству 4': 4') вычислительно невозможно найти любую пару x'!=x, такой что H(x')=H(x).

Поскольку из свойств 1–2 следует, что множество определения хэш-функции значительно шире множества значений, то коллизии должны существовать. Свойство 4 требует, чтобы найти их для заданного значения х было практически невозможно. Требование 4' говорит о том, что у сильной хэш-функции вычислительно невозможно вообще найти какую-либо коллизию.

Хэш-функцией с ключом (MAC) называется функция H(k,x), удовлетворяющая свойствам:

1. аргумент хфункции H(k, x)может быть строкой бит произвольной длины;
2. значение H(k, x)должно быть строкой бит фиксированной длины;
3. при любых kи xлегко вычислить H(k, x);
4. для любого хдолжно быть трудно вычислить H(k, x),не зная k;
5. должно быть трудно определить kдаже при большом числе неизвестных пар {x, H(k, x)}при выбранном наборе хили вычислить по этой информации H(k, x')для x'!=x.

Зачем нужна хэш-функция? Дело в том, что многие криптографические преобразования (в частности, вычисление и проверка электронной цифровой подписи, ЭЦП) выполняются над данными фиксированного размера. Поэтому перед просталением электронной подписи под многомегабайтным файлом обычно рассчитывают значение хэш-функции от него, а уже от этого значения считают ЭЦП. Кроме того, удобно, например, пароли в базе хранить не в открытом виде, а в хэшированном (так сделано во всех юниксах).

Некоторые алгоритмы хэш-функций:

• MD 2.Message Digest. Алгоритм криптографической сверки. Порождает 128- bit блок от сообщения произвольной длины.
• MD 4.Другой алгоритм свертки. Порождает 128-bit блок.
• MD 5.Существенно переделанный MD 4. Автор тот же – Риверст.
• SHA.Результирующий хэш равен 160-bit.
• ГОСТ Р34.11–94.Российский алгоритм. Длина свертки – 256 бит (очень удобно для формирования по паролю ключа для ГОСТ 28147–89).

2. Алгоритм SHA.

Функции

• SHA-1
• SHA-224, SHA-256
• SHA-384, SHA-512, SHA-512/224, SHA-512/384

SHA-1 использует последовательность нелинейных функций f₀ , f₁ ,…, f₇₉. Каждая функция f_t, где 0 ≤ t < 79, оперирует тремя 32-битными переменными: x, y, и z, в результате возвращая одно 32-битное слово. В алгоритме SHA-1 используется следующий набор нелинейных функций f_t (x, y, z):
00 ≤ t ≤ 19 Ch(x, y, z) = (x AND y) XOR ( NOT x AND z)
20 ≤ t ≤ 39 Parity(x, y, z) = x XOR y XOR z
40 ≤ t ≤ 59 Maj(x, y, z) = (x AND y) XOR (x AND z) XOR (y AND z)
60 ≤ t ≤ 79 Parity(x, y, z) = x XOR y XOR z

Булева алгебра.
Обратите внимание, что, например, функцию Ch может выразить по-другому:
z XOR (x AND (y XOR z))
Результат не изменится. В различных реализациях алгоритма такие варианты можно встретить.

Константы

• SHA-1
• SHA-224, SHA-256
• SHA-384, SHA-512, SHA-512/224, SHA-512/384

Константы K_t
00 ≤ t ≤ 19 0x5a827999
20 ≤ t ≤ 39 0x6ed9eba1
40 ≤ t ≤ 59 0x8f1bbcdc
60 ≤ t ≤ 79 0xca62c1d6

(Если вас заинтересовал вопрос, откуда взялись эти числа, то укажем их источник:
0x5A827999 = 2√/4, 0x6ED9EBA1 = 3√/4, 0x8F1BBCDC = 5√/4, 0xCA62C1D6 = 10−−√/4; все умножено на 2³²).

Предварительная обработка

Дополнение сообщения

Цель – сделать сообщение кратным 512 или 1024 бит, зависит от выбранного алгоритма SHA. Дополнение может быть выполнено перед процедурой вычисления хэша, или в ходе выполнения хэша, но до обработки блока(ов), который (ые) будут содержать дополнение.

• SHA-1, SHA-224, SHA-256
• SHA-384, SHA-512, SHA-512/224, SHA-512/384

Предположим, что длина сообщения M равна l бит. Сначала в конец сообщения добавляется «1», а затем нули - в количестве k - так, чтобы размер полученного сообщения был на 64 разряда меньше числа, кратного 512 (l+1+k = 448 mod 512). Далее, к полученному результату добавляется 64-битовое представление размера l исходного сообщения М. Например, (ASCII текст) у нас есть сообщение «abc», длиной 8 * 3 = 24 бита. Добавляем к сообщению «1», затем 448 - (24 +1) = 423 бит «0», и в конце 64-битовое представление размера 24 = 00…011000. В итоге получим 512-битовое сообщение вида:

2. Разбиение дополненного сообщения на M-битные блоки.

Дополненное сообщение разбивается на N M-битных блоков.

• SHA-1, SHA-224, SHA-256
• SHA-384, SHA-512, SHA-512/224, SHA-512/384

Дополненное сообщение разбивается на N 512-битовых блоков: M⁽¹⁾, M⁽²⁾ … M^(N). Т.к. 512 бит можно выразить как 16 (шестнадцать) 32-битных слов, то первые 32 бита i-го блока сообщения обозначим M₀⁽ⁱ⁾, следующие 32 бита M₁⁽ⁱ⁾, и так дойдем до M₁₅⁽ⁱ⁾.

Вычисление хэша

• SHA-1
• SHA-256
• SHA-224
• SHA-512
• SHA-384
• SHA-512/224
• SHA-512/256

В алгоритме сложение "+" происходит по модулю 2³².

For i = 1 to N:
{
1. i-й блок сообщения с помощью приведенного далее алгоритма
преобразуется из 16 слов размером в 32 разряда (с М₀⁽ⁱ⁾ по М₁₅⁽ⁱ⁾)
в 80 слов размером 32 разряда (с W₀ по W₇₉):
W_t = M_t, для t = 0..15
W_t = ROTL(W_t-3 XOR W_t-8 XOR W_t-14 XOR W_t-16, 1), для t = 16..79
(Интересно, что в первоначальном варианте спецификации SHA (алгоритм SHA-0) не было
циклического сдвига влево ROTL(x, 1))

2. Инициализируем переменные a,b,c,d,e.
a = H0^(i-1)
b = H1^(i-1)
c = H2^(i-1)
d = H3^(i-1)
e = H4^(i-1)

3. Главный цикл функции сжатия
For t = 0 to 79
TEMP = ROTL(a, 5) + f_t(b,c,d) + e + W_t + K_t
e = d
d = c
c = ROTL(b, 30)
b = a
a = TEMP

4. Считаем промежуточное хэш-значение
H0⁽ⁱ⁾ = (H0^(i-1) + a)
H1⁽ⁱ⁾ = (H1^(i-1) + b)
H2⁽ⁱ⁾ = (H2^(i-1) + c)
H3⁽ⁱ⁾ = (H3^(i-1) + d)
H4⁽ⁱ⁾ = (H4^(i-1) + e)
}

Результирующее хэш-значение – 160-битный дайджест сообщения:
H0^(N) || H1^(N) || H2^(N) || H3^(N) || H4^(N) (5 слов * 32 бита = 160 бит)
Внимание: порядок байт в каждом слове "big-endian"

Операции над словами (32-битными).
ROTL - циклический сдвиг влево на n бит:
ROTL(x, n) = (x « n) | (x » (32-n))

3. Стандарт получения хэш-функции - ГОСТ Р34.11-94.

Билет

1. Электронная цифровая подпись.

2. Стандарт DSS.

3. ГОСТ Р34.10-94 – стандарт цифровой подписи.

Билет

1. Защита программного обеспечения от исследования

2. Алгоритм Евклида нахождения наибольшего общего делителя.

3. Способы вычисление обратных чисел.

Билет

1. Расширенный алгоритм Евклида.

2. Алгоритмы цифровой подписи

3. Управ­ле­ние клю­ча­ми

Билет

Билет

1. Назовите основные понятия информационной безопасности компьютерных систем.

Билет

1. Что по­ни­ма­ет­ся под на­ко­п­ле­ни­ем клю­чей?

2. Как на­зы­ва­ют­ся клю­чи, за­шиф­ро­вы­ваю­щие клю­че­вую ин­фор­ма­цию?

Билет

1. Что может сделать на­рушитель через Internet?

Билет

Билет

1. Что представляет собой рассеивание?

2. Каким способом достигаются эффекты рас­сеивания и перемешивания?

3. Как выполняется функция шифрования?

Билет

1. Цель использования многоалфавитной подстановки.

2. Назовите традиционные методы шифрования

3. Назовите биграммные шифры

Билет

Билет

Назначение функции Эйлера?

Билет

1. Асимметричные криптоситемы.

2. Перечислите способы нахождения обратных чисел.

3. Для чего используется расширенный алгоритм Евклида?

Информационная безопасность и защита информации

Билет

1. Генерация последовательностей ПСЧ. Параметры генератора.

ГПСЧ не являются истинно случайными, поскольку генерируют последовательность чисел по некоторому алгоритму.

Основные характеристики алгоритма псевдослучайной генерации: начальное значение и период.

Начальное значение требуется по той причине, что обычно следующие числа зависят от предыдущих (рекуррентные соотношения). Вспомните: в любом адекватном рекуррентном соотношении есть некое граничное условие, например, если факториал представлять как n! = n * (n-1)!, то 0! = 1 - граничное условие. Другое пример - числа Фибоначчи: f(0) = f(1) = 1 - граничное условие, f(n) = f(n - 1) + f(n - 2) - рекуррентное соотношение. Каждый запросто может придумать другие - самопальные - рекуррентные соотношения...

Период - наименьшее T такое, что гарантированно X(i) = X(i + T), где i - целое неотрицательное (ведём нумерацию элементов последовательности с нуля), X(i) - i-ый член последовательности. Иначе говоря, псевдослучайная последовательность представляет собой серию повторяющихся групп из T чисел. Например, {2, 3, 0, 1, 2, 3, 0, 1, 2, ...} - здесь период T = 4, начальное значение X(0) = 2.

Зная алгоритм ГПСЧ и начальное значение, легко восстановить любое число X(i).

А теперь сформулируем требования, по которым в криптографии создаются ГПСЧ:

1. Псевдослучайная последовательность, выдаваемая ГПСЧ, должна иметь как можно больший период. Чем секретнее данные, тем больший период желательно иметь.
2. Зная любой фрагмент последовательности, выдаваемой генератором, злоумышленник не должен иметь эффективной возможности найти начальное значение, загруженное в генератор.
3. Зная любой фрагмент последовательности, выдаваемой генератором, злоумышленник не должен иметь возможности получить достоверную информацию о предыдущих или последующих элементах последовательности.
4. Ну и, разумеется, хотелось бы повыше скорость работы генератора. К сожалению, это несколько противоречит тому, что требуется как можно более высокая защищённость.

Требования 2 и 3 можно считать требованиями непредсказуемости.

Существуют истинно случайные генераторы. Примером такого может быть, например, игральный куб без смещённого центра тяжести и прочих жульнических штучек. Но в криптографии принято использовать ГПСЧ, поэтому их касаться не будем.

2. DES стандарт. Режим электронной кодовой книги.

Стандарт шифрования данных (DES)— блочный шифр с симметричными ключами, разработан Национальным Институтом Стандартов и Технологии (NIST – National Institute of Standards and Technology).

DES (Data Encryption Standart) — Симметричный алгоритм шифрования, в котором один ключ используется, как для шифрования, так и для расшифрования данных. DES разработан фирмой IBM и утвержден правительством США в 1977 году как официальный стандарт (FTPS 46-3). DES имеет блоки по 64 бит и 16 цикловую структуру сети Фейстеля, для шифрования использует ключ с длиной 56 бит. Алгоритм использует комбинацию нелинейных (S-блоки) и линейных (перестановки E, IP, IP-1) преобразований. Для DES рекомендовано несколько режимов:

· режим электронной кодовой книги (ECB — Electronic Code Book),

· режим сцепления блоков (СВС — Cipher Block Chaining),

· режим обратной связи по шифротексту (CFB — Cipher Feed Back),

· режим обратной связи по выходу (OFB — Output Feed Back).