Статистическая теория решений

Задача статистической теории решений, если ее излагать в терминах РТС, состоит в следующем. На вход системы поступает наблюдение {u(t),tÎ(0,T)}, представляемое обычно вектором наблюдений 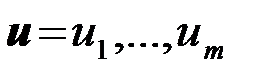(вектором отсчетов). Наблюдение образовалось из одного из сигналов { 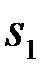, ,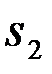..., 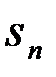} после того, как на него наложились помехи, а также, возможно, произошли искажения при прохождении через статистически неоднородную среду распространения. 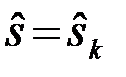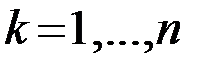Система (получатель информации) по наблюдению должна принять оптимальное решение , о том, какой именно сигнал из возможного множества { 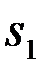, ,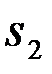..., 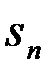} присутствует в наблюдении . Описанная задача в теории РТС называется задачей различения.

В терминах общей теории статистических решений вместо наблюдения речь идет о случайной последовательности 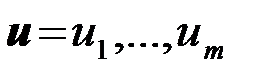например, о результате эксперимента или о совокупности признаков, представляющих собой случайные величины, характеризующие некоторые явления 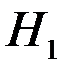,..., . 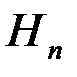Получатель информации 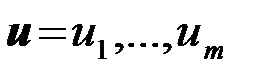, должен сделать оптимальный выбор между 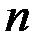конкурирующими гипотезами 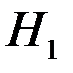,..., 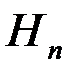- принять оптимальное решение .

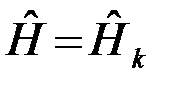Применения теории статистических решений весьма многочисленны - это техническая диагностика и дефектоскопия, медицинская диагностика, распознавание и классификация образов и многое другое. Вместе с тем идеология теории общая для всех этих приложений. Для решения поставленной задачи должны быть разработаны соответствующие математические модели явлений, позволяющие определить условные плотности вероятности p( | 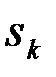). В байесовской теории решений, кроме того полагается, что посылка того или иного сигнала из ансамбля { 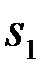,..., 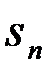}(в общем случае реализация той или иной гипотезы {H₁,...,H_n}) является случайным событием с заданными априорными вероятностями P₁,...,P_n реализации каждого события.

Для того, чтобы определить оптимальный алгоритм решений (оптимальную систему обработки наблюдений ), необходимо сформулировать критерий качества (качественный показатель), по которому можно было бы судить, какая система лучше, а какая хуже. В теории решений Байеса каждой паре ситуаций: 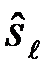, 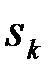( 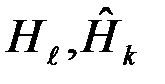): истинное значение сигнала (гипотезы) - принятое решение, ставится в соответствие некоторая количественная величина 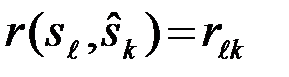, называемая функцией потерь и характеризующая убыток, потери или стоимость, которую следует уплатить за принятое решение 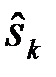( 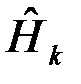), когда истинно 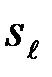( 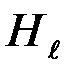). Решение 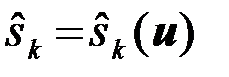представляет собой случайное событие, так как является функцией случайного вектора наблюдений u. Кроме того, случайным событием с априорной вероятностью P_k =P( 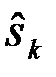) является посылка каждого из сигналов 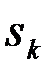(реализация каждой из гипотез 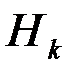). Поэтому функция потерь 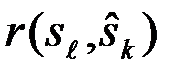также представляет собой случайную величину, различную в различных реализациях ситуаций 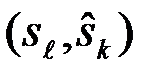, и непосредственно определять качество системы не может. Качество системы характеризуется математическим ожиданием функции потерь r - ее статистическим средним, взятым по всем возможным принимаемым решениям ( 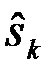, ) и по всем возможным посылаемым сигналам ,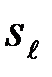

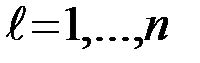
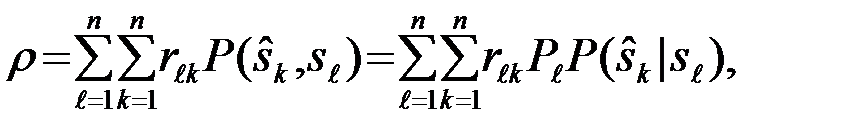(4.1.1)

где 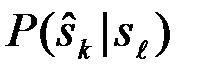- условная вероятность принятия решения 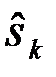, при условии, что послан сигнал .

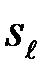Величина r называется средним риском. Оптимальным считается правило решений 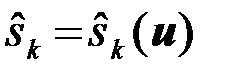и соответственно система обработки наблюдений , которые обеспечивают минимальное значение среднего риска r=min.

В задаче различения сигналов обычно используется простая функция потерь, приписывающая нулевые потери всем правильным решениям и одинаковые потери, равные 1, всем ошибочным решениям

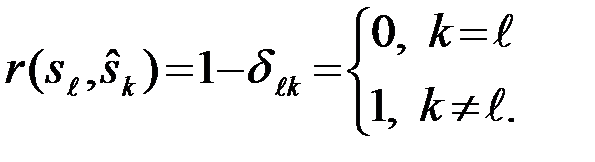(4.1.2)

Соответствующий средний риск получается равным

(4.1.3)

В частном случае, когда 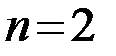(различение 2-х сигналов) возможны 4 ( 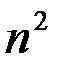) ситуации: 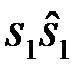, , 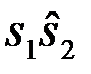, 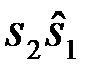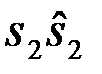причем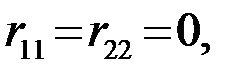 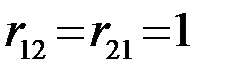и средний риск

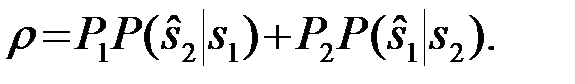(4.1.4)

Наиболее простым и распространенным типом цифровых сигналов являются сигналы КИМ. Именно этим сигналам будет уделено основное внимание. В системах с сигналами КИМ на каждом элементарном временном интервале на вход приемной системы поступают в смеси с помехами двоичные сигналы. Информационный параметр сигналов может принимать одно из двух значений, соответствующих передаче двоичного числа aÎ(0,1). В конце каждого элементарного временного интервала система принимает решение о том, какое сообщение 0 или 1 передается на данном интервале. В результате прием цифровых сигналов сводится к задаче различения двух сигналов. На этом простейшем примере изучим математический аппарат и основные закономерности теории различения сигналов. Полученные закономерности в конце главы будут обобщены на примере различения M- сигналов.