Стационарные случайные процессы

Если вся совокупность условий образования СП во времени не меняется, то процесс имеет однородный во времени характер и называется стационарным СП. В качестве примера приведем ток дробовых шумов лампы, который имеет характер стационарного СП при условии, что все факторы, влияющие на процесс (напряжения на электродах, температура катода и др.) во времени не меняются.

Математически стационарность определяется следующим образом. СП является стационарным, если его многомерная ПВ любого порядка не меняется при изменении всех отсчетных моментов времени t₁, t₂, ..., t_n на одну и ту же произвольную величину t

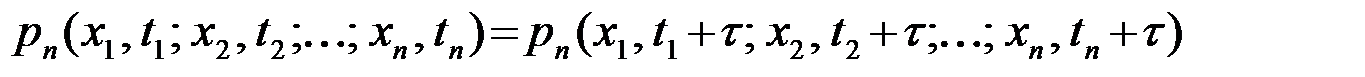.(3.4.1)

Иначе говоря, для стационарного СП совместное распределение сечений X(t₁+t), X(t₂+t),.., X(t_n+t) одно и то же при любом временном сдвиге t.

Стационарные СП по определению однородны при любых значениях времени t. Соответственно областью определения стационарных СП является бесконечный интервал tÎ(-¥,¥), тогда как реальные сигналы отличны от нуля только на конечных интервалах. Поэтому математические модели стационарных СП представляют собой идеализации сигналов и помех, однородных на достаточно больших интервалах T.

Наибольший практический интерес представляет применение условий стационарности к распределениям двух первых порядков и к характеристикам СП, используемым в корреляционной теории.

Применение условий стационарности (1) к ПВ первого порядка дает:

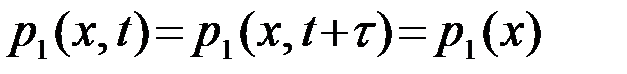,(3.4.2)

т.е. ПВ p₁( ) в любой отсчетный момент t+t (t - произвольное) получается одной и той же и, следовательно, от времени t вообще не зависит. Поэтому математическое ожидание m_x(t) и дисперсия стационарного СП, определяемые ПВ (2), в любой отсчетный момент времени t имеют одно и то же значение - являются постоянными величинами

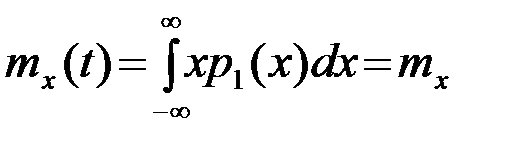,(3.4.3)

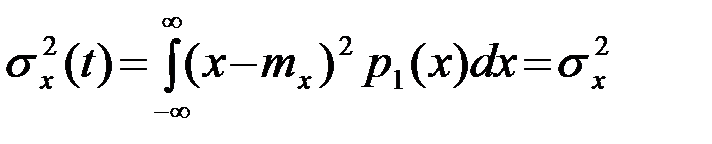.(3.4.4)

Далее применяем условие стационарности (1) к ПВ второго порядка

.

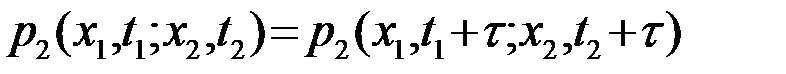Последнее равенство сохраняется при любом t, в частности при t= -t₁. При этом

.

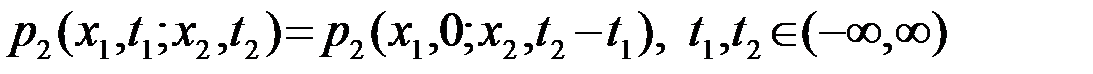Это значит, что ПВ второго порядка стационарного СП зависит не от каждого отсчетного момента t₁ и t₂ в отдельности, а от их разности t₂-t₁ , т.е. является функцией не 4-х, а 3-х переменных: значений процесса x₁ и x₂ в отсчетные моменты t₁, t₂ и разности t₂-t₁

.(3.4.5)

Корреляционная функция стационарного СП

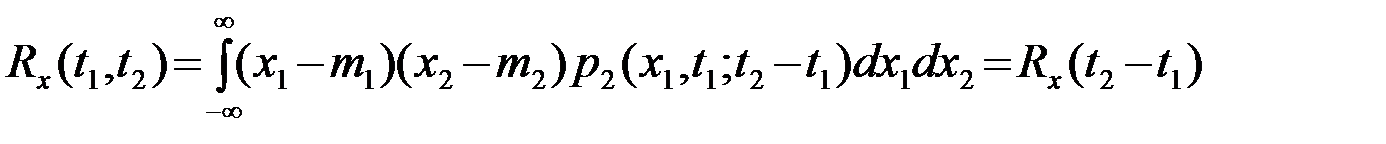(3.4.6)

является функцией одной переменной - разности отсчетных моментов времени t₂-t₁. В силу условия симметрии (3.2.4) корреляционная функция (вещественного) стационарного СП - четная функция разности отсчетных моментов t₂-t₁=t

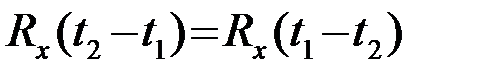или (3.4.7)

Функция R_x(t) имеет абсолютный максимум в нуле

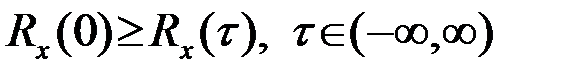,(3.4.8)

что следует из неравенства

.

Таким образом, корреляционная функция стационарного СП является четной функцией своего аргумента t=t₂-t₁, и имеет абсолютный максимум, равный дисперсии процесса 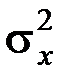в точке t=0. Отметим также, что основным типом физических СП (например, естественных помех радиоприему) является СП со сравнительно быстро убывающей (не обязательно монотонно) по мере роста t функцией R_x(t). В качестве примера рассмотрим корреляционную функцию модели телеграфного сигнала.

Пример 3.4.1. Модель сигнала x(t) задается "прямоугольной" волной (рис.3.4). Значения сигнала могут принимать 2 значения A₀ и -A₀. При этом перемены знака (переходы) внутри произвольного интервала (t, t+t) происходят в независимые моменты времени, а их число n подчиняется закону Пуассона, согласно которому

,(3.4.9)

где l - среднее число переходов за 1с.

Рис. 3.4

Согласно исходным условиям примера

.

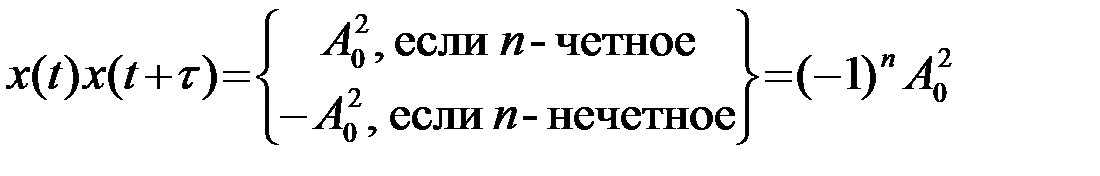Соответственно,

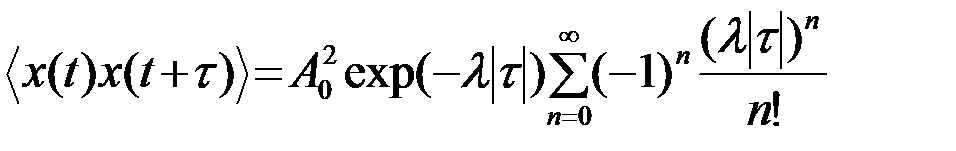
и

.

Аналогично вид импульса имеет функция R_x(t), когда СП формирует хаотическая последовательность сравнительно коротких импульсов. В зависимости от того, видеоимпульсы или радиоимпульсы формируют СП, корреляционная функция также имеет вид видео - или радиоимпульса (рис.3.5). В практических задачах оценки временного сдвига между сечениями СП X(t₁) и X(t₂), для которых следует учитывать наличие корреляции, используется параметр t_к, называемый временем корреляции СП и равный половине ширины корреляционной функции.

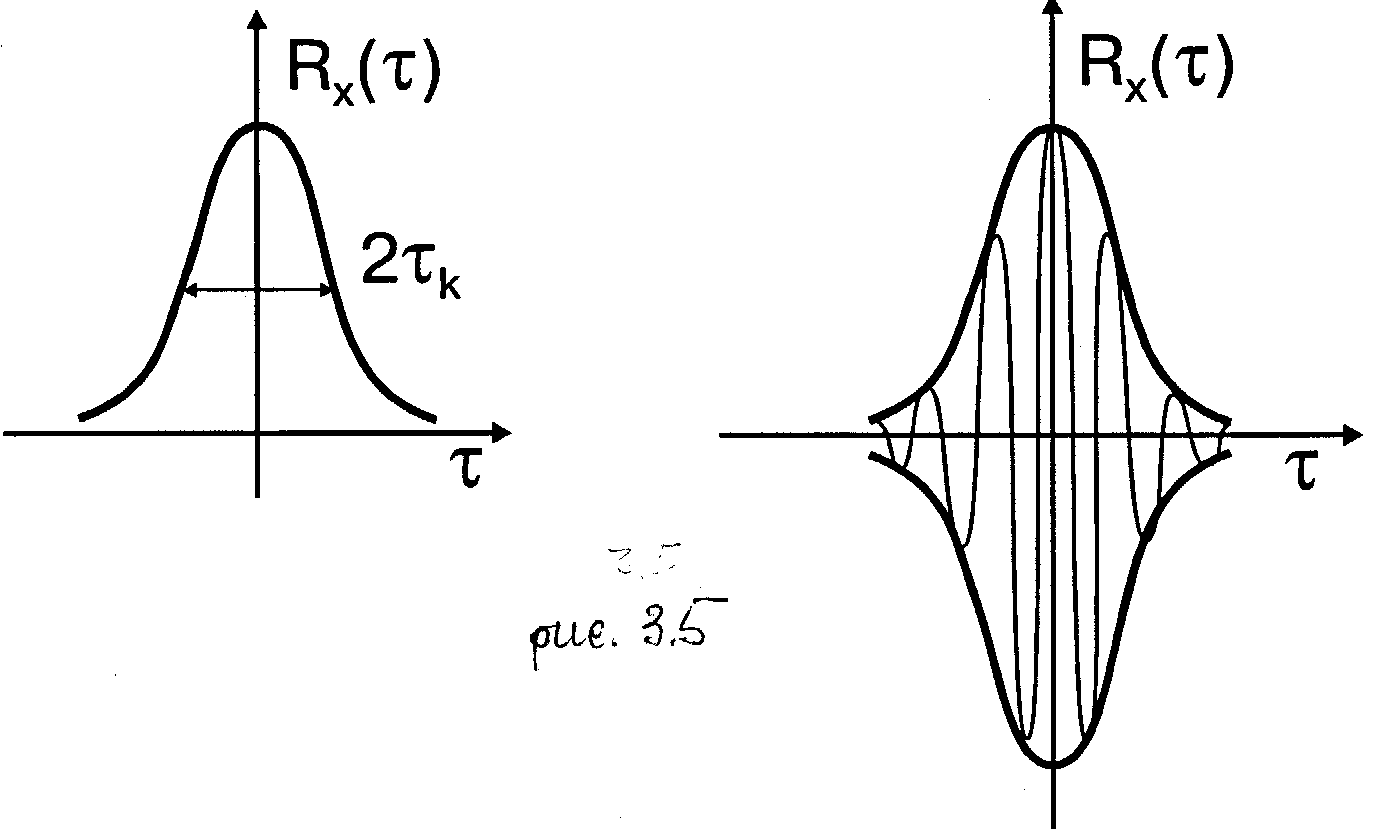
Рис. 3.5

Другой вид корреляционной функции R_x(t) стационарного СП формируется квазидетерминированным процессом, представляющим собой, например, гармоническое колебание

(3.4.10)

со случайными независимыми амплитудой A и начальной фазой j, распределенной равновероятно в интервале (0,2p)

(3.4.11)

Совершенно аналогично, если СП представляет собой конечную сумму n независимых процессов вида (10) с различными частотами f_i и независимыми (A_i, j_i), i=1,2,...n, то

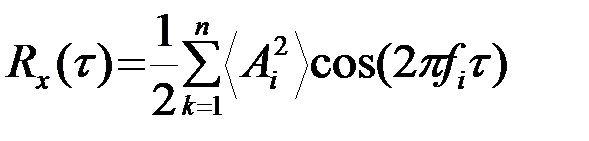.(3.4.12)

В рамках корреляционной теории условиями стационарности являются: постоянство математического ожидания (3) и зависимость корреляционной функции не от двух аргументов t₁ и t₂ , а от одного t=t₂-t₁ (6). В общем случае эти условия являются необходимыми, но не достаточными условиями стационарности в смысле (1). Поэтому в отличие от строгих условий стационарности (1), называемых условиями стационарности в узком смысле, условия (3), (6) называют условиями стационарности в широком смысле. Важность условий стационарности в широком смысле возрастает в связи с тем, что для гауссовских процессов эти условия гарантируют строгую стационарность в смысле (1), так как математическое ожидание и корреляционная функция исчерпывающе определяют гауссовский процесс.

Стационарный СП называется эргодическим, если любая его характеристика, полученная усреднением по ансамблю реализаций (статистическим усреднением), совпадает с этой же характеристикой, полученной усреднением по времени в пределах одной реализации СП. Рассмотрим представляющие наибольший интерес временные аналоги основных характеристик СП. Положим, имеется некоторая реализация x(t,w) СП X(t). Введем для этой реализации следующие характеристики.

Среднее по времени

(3.4.13)

представляет собой постоянную составляющую реализации x(t,w), которая от времени не зависит, но в общем случае для различных реализаций получается различной (зависит от w). Здесь и в дальнейшем черта над функцией времени означает операцию усреднения этой функции по времени

.(3.4.14)

Определяется центрированная реализация (переменная составляющая реализации)

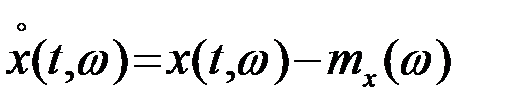.(3.4.15)

Временная корреляционная функция представляет собой результат усреднения по времени произведения двух сечений центрированной реализации СП

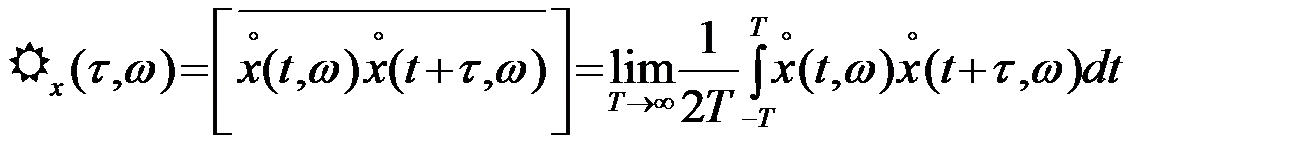(3.4.16)

и зависит от временного сдвига t между сечениями. Заметим, что определения временной корреляционной функции R( ) для функций времени с ограниченной энергией (2.2.15) и для функций с неограниченной энергией (16) несколько отличаются друг от друга. В общем случае временная корреляционная функция для различных реализаций (для различных w) получается различной.

Средняя по времени мощность переменной составляющей

(3.4.17)

и полная средняя по времени мощность реализации

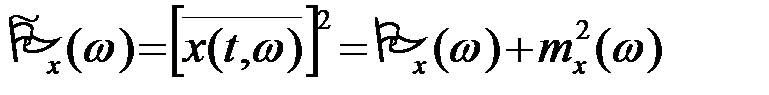(3.4.18)

также для различных реализаций различны.

Для эргодических СП по определению временные характеристики совпадают с соответствующими статистическими характеристиками

.(3.4.19)

Так как временная характеристика в (19) не зависит от t, а статистическая (3.2.1) - от w, то их равенство удовлетворяется тогда, когда среднее значение (19) и (3.2.1) является постоянной величиной, независящей ни от t, ни от w.

Аналогично

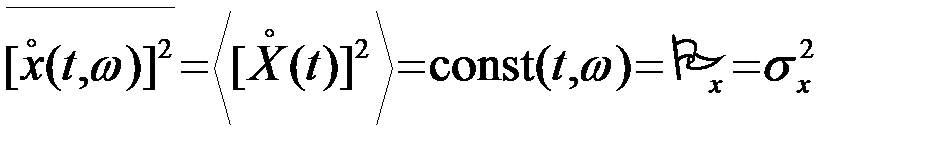.(3.4.20)

Равенство корреляционных функций R_x(t,w) и R_x(t,t+t)

(3.4.21)

возможно тогда, когда каждая из этих характеристик зависит только от разности своих временных аргументов. Равенство (20) является частным случаем (21) при t=0.

Не всякий стационарный случайный процесс эргодический.

Пример 3.4.2.

, (3.4.22)

где A(w) и j(w) - независимые случайные величины, причем j распределено равновероятно в интервале (0,2p).

Находим основные характеристики процесса (22)

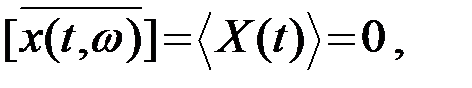(3.4.23)

(3.4.24)

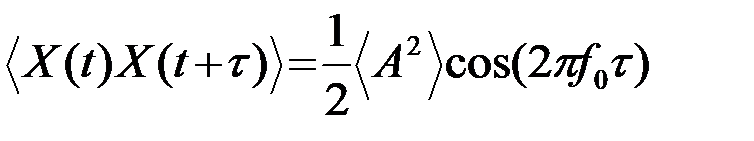. (3.4.25)

Процесс (22) стационарен, во всяком случае, в широком смысле: математическое ожидание (23) - постоянная величина (нуль), а корреляционная функция (25) зависит от разности отсчетных моментов. Однако процесс неэргодический, так как временная корреляционная функция (24) для различных реализаций получается различной (зависит от A(w)).

Процесс может быть эргодическим относительно одних характеристик и неэргодическим относительно других. В связи с этим вводится понятие эргодичности в широком смысле, когда условия эргодичности выполняются только для среднего значения (19) и корреляционной функции (21), в отличие от эргодичности в узком смысле, когда условия эргодичности выполняются для любых характеристик процесса.

Чтобы стационарный СП X(t) был эргодическим любая его реализация x(t,w) должна отражать свойства всего ансамбля {x(t,w), wÎW}. Для пояснения такой возможности положим, что реализация стационарного СП разбита на отрезки конечной длительности T: ..., (-T,0), (0,T), (T,2T),... Если это множество отрезков можно рассматривать, как различные независимые реализации СП, то фактически есть возможность в пределах одной реализации провести усреднение по ансамблю реализаций. Для такого разбиения необходимо, чтобы корреляционная функция R_x(t) процесса X(t) практически обращалась в нуль, при некотором значении t

.(3.4.26)

В практических приложениях свойство эргодичности широко используется. Благодаря этому свойству для экспериментального определения различных характеристик эргодических процессов экспериментатору нет необходимости изучать большую совокупность реализаций, которой он, как правило, не располагает. Достаточно одной реализации, наблюдаемой в течение достаточно длительного промежутка времени. Приведем два примера определения статистических характеристик эргодического процесса.

Пример 3.4.3. Принцип действия одного из типов коррелометров - прибора для измерения корреляционной функции поясняется на схеме рис.3.6.

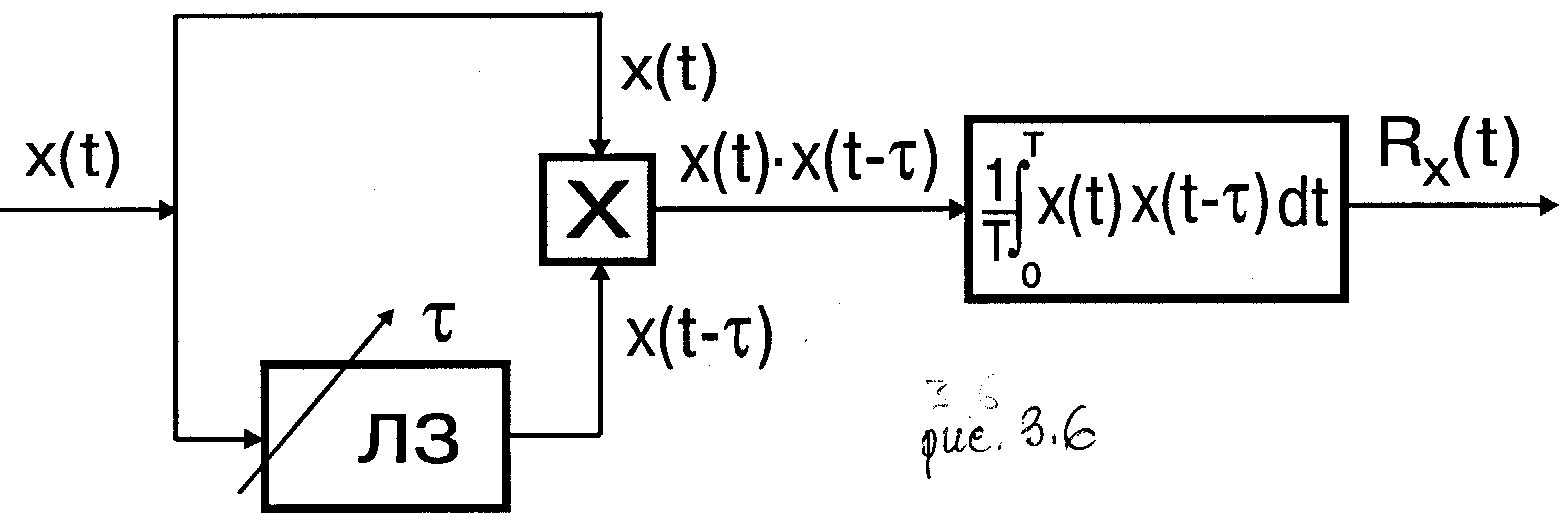
Рис. 3.6

Входной процесс x(t) непосредственно и через линию задержки ЛЗ с переменным временем задержки tподводится к перемножителю (x). С выхода перемножителя колебание x(t)x(t-t) поступает на интегратор, осуществляющий операцию

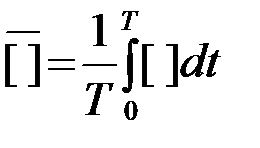
над подводимым к нему колебанием [ ]. В результате при достаточно большом времени интегрирования (усреднения) T выходной эффект прибора практически воспроизводит временную корреляционную функцию R_x(t₁) при данном времени задержки t=t₁. Изменяя время задержки t₁ на t₂,...,t_n последовательно по точкам строят временную корреляционную функцию R_x(t), совпадающую для эргодических процессов с корреляционной функцией R(t). Если процесс x(t) кратковременный, его предварительно запоминают (записывают), а затем многократно подают на вход коррелометра для получения последовательности значений R_x(t₁),...,R_x(t_n).

Пример 3.4.4. Определяется одномерная ПВ p(x) эргодического процесса X(t). Используется нелинейное преобразование y(t)=f[x(t)] реализации процесса x(t), в котором функция f(x) равна

Реализации процессов x(t) и y(t) показаны на рис.3.7,а и 3.7,б соответственно.

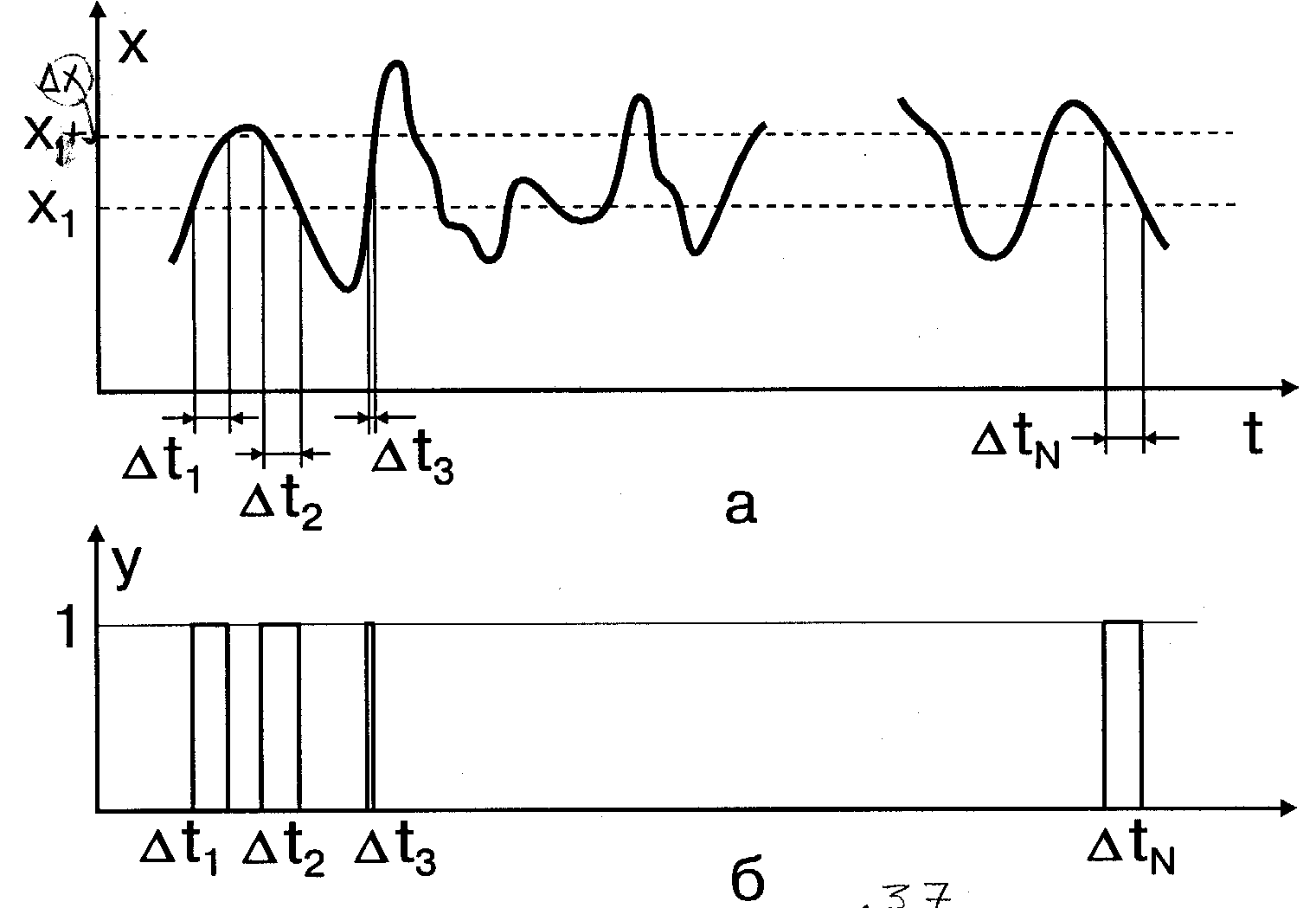
Рис. 3.7

Найдем среднее по времени и по ансамблю реализаций функции y(t)

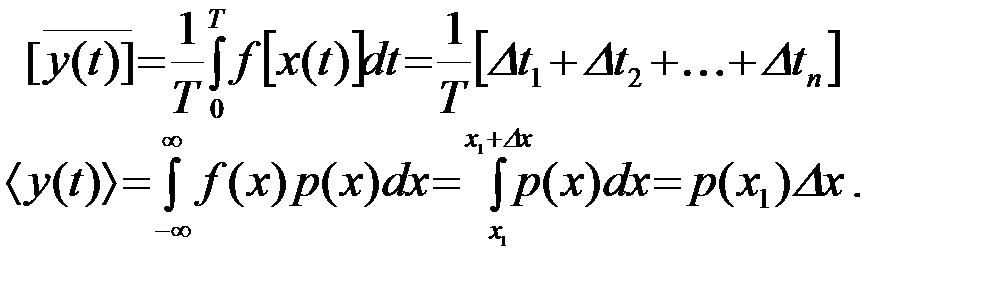
В силу эргодичности процесса x(t), а, следовательно, и y(t), среднее по времени 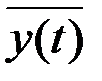равно математическому ожиданию , откуда

.

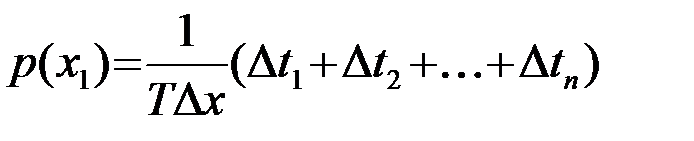Изменяя значение x₁ на x₂,...,x_n, по точкам строят одномерную ПВ p(x).