Дифференциальное исчисление функции одной переменной
Дифференциальное исчисление функции одной переменной
1. Введение
Математический анализ – ветвь математики, оформившаяся в ХVIII столетии и включающая в себя две основные части: дифференциальное и интегральное исчисления. Производная функции – одно из основных математических понятий дифференциального исчисления. Анализ возник благодаря усилиям многих математиков (в первую очередь И. Ньютона и Г. Лейбница) и сыграл громадную роль в развитии естествознания – появился мощный, достаточно универсальный метод исследования функций, возникающих при решении разнообразных прикладных задач.
2. Числовая функция. Схема исследования функции.
(Смотри конспекты по теме «Степенная функция»)
1) Область определения функции.
2) Множество значений функции.
3) Четность, нечетность функции.
4) Монотонность функции.
5) Обратимость функции.
6) Нули функции.
7) Промежутки знакопостоянства функции.
8) Ограниченность функции.
Упражнения:
- Найти область определения функции:
а) 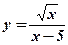 ; б)
; б) 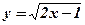 ; в)
; в) 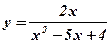 .
.
- Найти область определения функции: а)
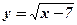 ; б)
; б) 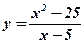 .
. - Выяснить, является ли функция четной или нечетной:
а) 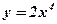 ; б)
; б) 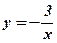 ; г)
; г) 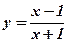 .
.
3. Понятие предела функции в точке.
Рассмотрим графики некоторых функций. Изучим поведение функций вблизи точки х0 , то есть в некоторой окрестности точки х0.
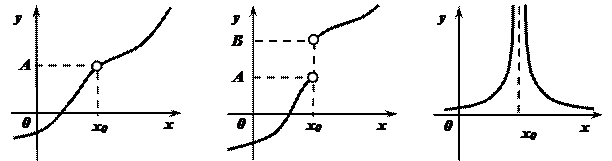 |
Рис. 1.  Рис. 2.
Рис. 2. 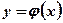 Рис. 3.
Рис. 3. 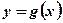
Функция  обладает свойством, отличающим ее от двух других функций.
обладает свойством, отличающим ее от двух других функций.
1. При приближении аргумента х к х0 слева и справа соответствующие значения функции 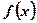 сколь угодно близки к одному и тому же числу А.
сколь угодно близки к одному и тому же числу А.
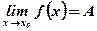
Этим свойством не обладают две другие функции.
2. При приближении аргумента х к х0 слева соответствующие значения функции 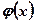 сколь угодно близки к числу А, а при приближении аргумента х к х0 справа соответствующие значения функции
сколь угодно близки к числу А, а при приближении аргумента х к х0 справа соответствующие значения функции 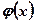 сколь угодно близки к числу В.
сколь угодно близки к числу В.
3. Функция 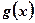 при приближении аргумента х к х0 слева и справа принимает различные значения.
при приближении аргумента х к х0 слева и справа принимает различные значения.
Вывод:Еслипри приближении аргумента х к х0 слева и справа точки с координатами 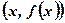 сколь угодно близки к точке с координатами
сколь угодно близки к точке с координатами 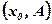 , то
, то 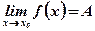 .
.
Пример: Имеет ли функция  предел в точках х1, х2, х3, х4, х5?
предел в точках х1, х2, х3, х4, х5?
 |
Ответ: Функция  имеет предел в точках х1, х3 ;
имеет предел в точках х1, х3 ;
функция  не имеет предела в точках х2, х4, х5.
не имеет предела в точках х2, х4, х5.
Замечание: 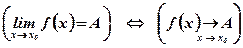
4. Определение функции непрерывной в точке и на промежутке
Понятие непрерывности функции удобно связать с представлением о графике этой функции как о «неразрывной» (сплошной) линии. Сплошной линией будем считать линию, начерченную без отрыва карандаша от бумаги.
Вопрос: Какие из данных функций являются непрерывными?

 Рис. 1. Рис. 2. Рис. 3.
Рис. 1. Рис. 2. Рис. 3.
Рис. 4. Рис. 5.
Ответ: Из данных функций непрерывной является функция, изображенная на рис. №3, так как ее график - «неразрывная» (сплошная) линия.
Вопрос: Какими свойствами обладает функция, изображенная на рис. №3, и не обладают другие функции?
Ответ:
1. Функция определена в точке х0. Это свойство не выполняется для функции, изображенной на рис. №1.
2. Существует конечный предел функции в точке х0. Это свойство не выполняется для функций, изображенных на рис. №2, 5.
3. Предел функции в точке х0 равен значению функции в этой точке, то есть 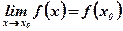 . Это свойство не выполняется для функции, изображенной на рис. №4.
. Это свойство не выполняется для функции, изображенной на рис. №4.
Свойства, которые выполняются для функции, изображенной на рис. №3, и дают возможность дать определение функции непрерывной в точке х0.
Определение: Функция  называется непрерывной в точке х0, если
называется непрерывной в точке х0, если 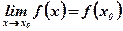 .
.
Замечание: Если функция является непрерывной в точкех0,то точка х0 называется точкой непрерывности функции, если функция не является непрерывной в точкех0,то точка х0 называется точкой разрыва функции.
 Определение: Функция
Определение: Функция  называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала.
называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала.
5. Приращение аргумента, приращение функции
Пусть задана функция  ,
, 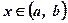 .
.
х0 – начальное значение аргумента,  ;
;
х– конечное значение аргумента, 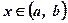 ;
;
f (х0) – начальное значение функции;
f(х0 +D х) – конечное значение функции.
Определение: Разность конечного и начального значений аргумента называется приращением аргумента. D х = х – х0
Определение: Разность конечного и начального значений функции называется приращением функции. D у = f(х0 +D х) – f (х0)
Замечание:
- Геометрически приращение аргумента D х– есть разность абсцисс точек графика функции, соответствующих конечному и начальному значениям аргумента.
- Геометрически приращение функции D у– есть разность ординат точек графика функции, соответствующих конечному и начальному значениям аргумента.
- Приращение аргумента и приращение функции могут быть как положительными, так и отрицательными.
6. Понятие производной функции. Физический смысл производной функции
Рассмотрим задачу о скорости изменения функции  , где х и у могут быть любыми физическими величинами.
, где х и у могут быть любыми физическими величинами.
х0 – начальное значение аргумента; f (х0) – начальное значение функции;
х0 +D х – конечное значение аргумента; f(х0 +D х) – конечное значение функции;
D у = f(х0 +D х) – f (х0) – приращение функции;

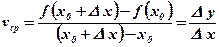
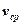 – средняя скорость изменения функции на интервале D х.
– средняя скорость изменения функции на интервале D х.
 – мгновенная скорость изменения функции, скорость изменения функции в точке х0.
– мгновенная скорость изменения функции, скорость изменения функции в точке х0.

Определение: Производной функции  в точке х0 называется предел отношения приращения D у функции в точке х0 к приращению D х аргумента при стремлении приращения аргумента к нулю.
в точке х0 называется предел отношения приращения D у функции в точке х0 к приращению D х аргумента при стремлении приращения аргумента к нулю.
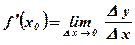
Вывод: Производная функции  в точке х0 есть скорость изменения функции в точке х0.
в точке х0 есть скорость изменения функции в точке х0.
Теорема: Производная постоянной функции у = с в любой точке  равна нулю.
равна нулю.
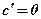
Теорема: Производная функции у = х в любой точке  равна единице.
равна единице.
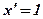 .
.
Замечание: Нахождение производной от данной функции называется дифференцированием.
7. Правила дифференцирования суммы, произведения, частного функций
Рассмотрим функцию  ,состоящую из двух других функций
,состоящую из двух других функций 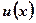 и
и  , имеющих производные на отрезке
, имеющих производные на отрезке 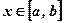 :
:
1)  ;
;
2)  ;
;
3)  .
.
Теорема №1: Производная суммы (разности) двух функций равна сумме (разности) производных этих функций. 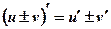
Пример: Вычислить производную функции 
 ;
;  .
.
Теорема №2: Производная произведения двух функций определяется по формуле: 
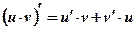
Следствие: Постоянный множитель можно вынести за знак производной: 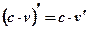 .
.
Доказательство: 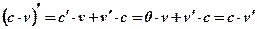 .
.
Пример: Вычислить производные функций:
-
 .
. 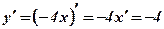 .
. -
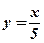 .
.  .
. -
 .
.

-
 .
.  ;
; 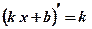 .
.
Упражнения:
1)  ;
;
2) 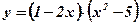 ;
;
3)  .
.
Производная степенной функции  при
при  вычисляется по формуле:
вычисляется по формуле:

Замечание: Формула  справедлива для степенной функции с любым показателем степени
справедлива для степенной функции с любым показателем степени 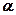 .
. 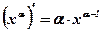 ,
, 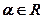
Пример: Вычислить производные функций:
-
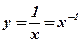 . Решение:
. Решение:  .
. -
 . Решение:
. Решение:  .
. -
 . Решение:
. Решение: 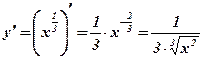 .
. -
 . Решение:
. Решение:  .
.
Вывод:  .
.
Упражнения: Вычислить производные функций:
1)  ; 2) ; 2) 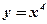 ; 3) ; 3)  ; ; | 4)  ; 5) ; 5)  ; ; | 6)  ; 7) ; 7)  . . |
Теорема №3: Производная частного двух функций определяется по формуле: 
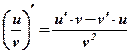
Следствия: 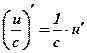 ;
; 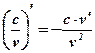
Пример: Вычислить производные функций:
1) 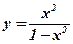 .
.

2)  .
.  .
.
3) 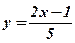 .
.  .
.
Упражнения: Вычислить производные функций:
1.  ; 2. ; 2. 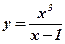 ; 3. ; 3.  ; ; | 4. 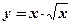 ; 5. ; 5.  ; 6. ; 6.  ; ; | 7. 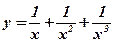 ; 8. ; 8.  ; 9. ; 9. 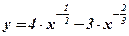 . . |
8. Понятие сложной функции
Правило дифференцирования сложной функции
Пусть функция  определена на множестве
определена на множестве  , а функция
, а функция 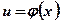 на множестве
на множестве  , причем для
, причем для 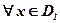 , соответствующее значение
, соответствующее значение 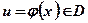 . Тогда на множестве
. Тогда на множестве  определена функция
определена функция  , которая называется сложной функцией от х(функцией от функции).
, которая называется сложной функцией от х(функцией от функции).
Переменную 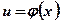 называют промежуточным аргументом сложной функции.
называют промежуточным аргументом сложной функции.
Пример:
-
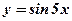 - тригонометрическая, линейная функция;
- тригонометрическая, линейная функция; 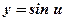 ,
, 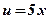 ;
; -
 - степенная, тригонометрическая функция;
- степенная, тригонометрическая функция;  ,
, 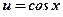 ;
;  - степенная, линейная функция;
- степенная, линейная функция;  ,
,  ;
;-
 - показательная, степенная функция;
- показательная, степенная функция; 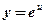 ,
, 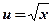 ;
;
Упражнения:
- Из каких элементарных функций состоят данные сложные функции:
1)  ; 2) ; 2) 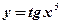 ; ; | 3) 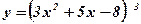 ; 4) ; 4)  . . |
- Из данных элементарных функций составить сложные функции:
1) 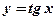 , , 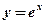 ; 2) ; 2) 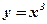 , ,  ; ; | 3) 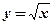 , , 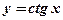 . 4) . 4) 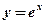 , ,  , , 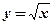 . . |
Вывод: Производная сложной функции равна произведению производных элементарных функций, ее составляющих.
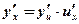
Пример: Вычислить производные функций:
1.  .
.
 - степенная, линейная;
- степенная, линейная; 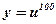 ,
,  .
.
 .
.
2.  .
.
 - степенная, квадратичная;
- степенная, квадратичная;  ,
,  .
.
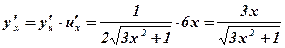 .
.
Упражнения: Вычислить производные функций:
1.  ; 2. ; 2. 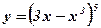 ; ; | 3.  ; 4. ; 4.  ; ; | 5.  ; 6. ; 6.  . . |
9. Производная показательной, логарифмической функций
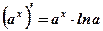
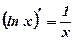
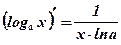
Пример: Вычислить производные функций:
1. 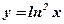 .
.  .
.
2.  .
.  .
.
3.  .
. 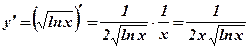 .
.
Пример: Вычислить производные функций:
1. 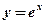 .
.  .
.
2.  .
. 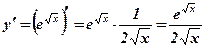 .
.
Упражнения: Вычислить производную функции:
1. 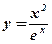 ; 2. ; 2. 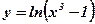 ; 3. ; 3.  ; ; | 4. 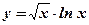 ; 5. ; 5.  ; 6. ; 6. 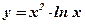 ; ; | 7. 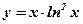 ; 8. ; 8.  . . |
10. Производные тригонометрических функций
Производные обратных тригонометрических функций
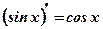 .
.
Пример: Вычислить производные функций:
1. 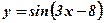 .
.  .
.
2. 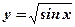 .
.  .
.
Задача: Вычислить производную функции 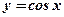 .
.
 .
. 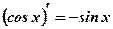 .
.
Задача: Вычислить производную функции  .
.

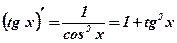 .
.
Упражнение: Вычислить производную функции  .
.
 .
.
Рис. 1. Рис. 2.
Замечание: Точки максимума и минимума функции называются точками экстремума (extremum – крайний), а значения функции в этих точках – экстремальными (максимальными и минимальными).
Установим необходимое условие существования экстремума.
Теорема Ферма: Если внутренняя точка х0 из области определения непрерывной функции  является точкой экстремума и в этой точке существует производная, то она равна нулю.
является точкой экстремума и в этой точке существует производная, то она равна нулю.
Замечание: Однако равенство нулю производной функции в точке х0 еще не дает права утверждать, что х0 –точка экстремума функции.
Пример:
- Функция
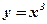 имеет производную
имеет производную 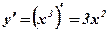 , которая обращается в нуль при х = 0. Но в этой точке функция
, которая обращается в нуль при х = 0. Но в этой точке функция 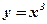 (кубическая парабола) экстремума не имеет.
(кубическая парабола) экстремума не имеет. - Функция
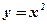 имеет производную
имеет производную 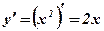 , которая обращается в нуль при х = 0. В этой точке функция
, которая обращается в нуль при х = 0. В этой точке функция 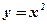 (парабола) имеет минимум.
(парабола) имеет минимум.
Определение: Значения аргумента х, при которых производная функции равна нулю или не существует, называются критическими точками этой функции.
Чтобы определить, имеет ли функция экстремум в данной точке, необходимо воспользоваться достаточными условиями существования экстремума.
Теорема: Значение аргумента х0 является точкой экстремума функции  , если производная
, если производная 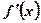 , равная нулю в точке х0, при переходе через х0 меняет знак. При перемене знака с «+» на «–» точка х0 является точкой максимума. При перемене знака с «–» на «+» точка х0 является точкой минимума. Если же производная
, равная нулю в точке х0, при переходе через х0 меняет знак. При перемене знака с «+» на «–» точка х0 является точкой максимума. При перемене знака с «–» на «+» точка х0 является точкой минимума. Если же производная 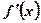 при переходе через х0 не меняет знака, то х0 не является точкой экстремума.
при переходе через х0 не меняет знака, то х0 не является точкой экстремума.
План исследования функции на монотонность и существование точек экстремума
1. Найти область определения функции.
2. Вычислить производную функции.
3. Найти критические точки функции, приравняв производную функции к нулю и решив полученное уравнение.
4. Определить знак производной функции слева и справа от критических точек.
5. Определить характер монотонности функции в полученных интервалах области определения функции и экстремумы функции, если они есть.
6. Вычислить значения функции в точках экстремума.
Пример: Исследовать на экстремум функцию 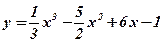 .
.
1. Найдем область определения функции 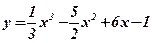 :
: 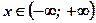 .
.
2. Вычислим производную функции: 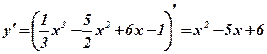 .
.
3. Найдем критические точки функции, то есть значения аргумента х, при которых производная функции равна нулю: 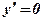 ;
; 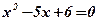 ;
; 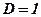 ;
; 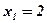 ;
; 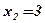 .
.
4. Определим знак производной слева и справа от критических точек 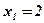 ;
; 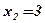 , и характер монотонности функции в полученных интервалах:
, и характер монотонности функции в полученных интервалах:
| х | 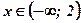 | 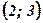 | 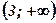 | ||
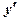 | + | - | + | ||
| у | ↑ | max | ↓ | min | ↑ |
5. Определим точки экстремума функции и экстремальные значения функции:
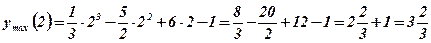 .
.
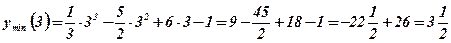 .
.
Ответ: 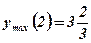 ;
; 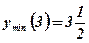 .
.
Упражнения: Исследовать на монотонность и существование точек экстремума функции:
|
|
|
14. Наибольшее и наименьшее значения функции на промежутке
Замечание:
- Точки максимума и минимума функции называют локальными экстремумами функции, так как речь идет об экстремальных значениях функции в окрестностях некоторых точек.
- Наибольшее и наименьшее значения функции на отрезке называют глобальными экстремумами функции.
Решение многих практических задач часто сводится к нахождению наибольшего и наименьшего значений непрерывной на отрезке функции.
Теорема Вейерштрасса: Непрерывная на отрезке 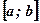 функция
функция  принимает на этом отрезке наибольшее и наименьшее значения.
принимает на этом отрезке наибольшее и наименьшее значения.
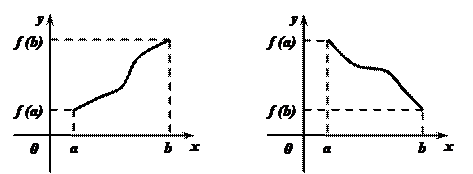 Для случая, когда функция
Для случая, когда функция  не только непрерывна на отрезке
не только непрерывна на отрезке 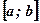 , но имеет на этом отрезке конечное число критических точек, укажем правило отыскания наибольшего и наименьшего значений функции
, но имеет на этом отрезке конечное число критических точек, укажем правило отыскания наибольшего и наименьшего значений функции  . Предположим, сначала, что
. Предположим, сначала, что  не имеет на отрезке
не имеет на отрезке 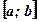 критических точек. Тогда она возрастает (Рис.1.) или убывает (Рис.2.) на этом отрезке, и, значит, наибольшее и наименьшее значения функции
критических точек. Тогда она возрастает (Рис.1.) или убывает (Рис.2.) на этом отрезке, и, значит, наибольшее и наименьшее значения функции  на отрезке
на отрезке 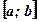 - это значения в концах a и b.
- это значения в концах a и b.
Рис.1. Рис. 2.
Пусть теперь функция  имеет на отрезке
имеет на отрезке 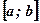 конечное числокритических точек. Эти точки разбивают отрезок
конечное числокритических точек. Эти точки разбивают отрезок 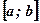 на конечное число отрезков, внутри которых критических точек нет. Поэтому наибольшее и наименьшее значения функции
на конечное число отрезков, внутри которых критических точек нет. Поэтому наибольшее и наименьшее значения функции  на таких отрезках принимаются в их концах, то есть в критических точках функции или в точках а и b.
на таких отрезках принимаются в их концах, то есть в критических точках функции или в точках а и b.
Вывод: Чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.
Пример: Найти наибольшее и наименьшее значения функции 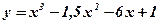 на отрезке
на отрезке 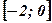 .
.
1) 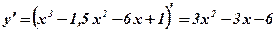 .
.
2) 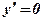 ;
; 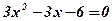 ;
; 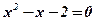 ;
; 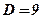 ;
;
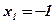 - критическая точка,
- критическая точка, 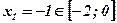 ;
;
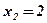 - критическая точка,
- критическая точка, 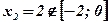 .
.
3) 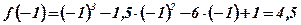 ;
;
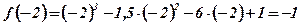 ;
;
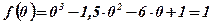 .
.
4) 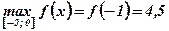 ;
; 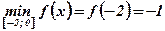 .
.
Ответ: 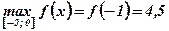 ;
; 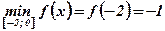 .
.
Упражнения:
- Найти наибольшее и наименьшее значения функции
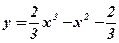 на отрезке
на отрезке 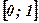 .
.
Изложенный метод поиска наибольшего и наименьшего значений функции применим к решению разнообразных прикладных задач. При этом действуют по следующей схеме:
1. Этап формализации: Задача «переводится» на язык функций. Для этого выбирается удобный параметр х, через который исследуемая величина выражается как функция 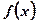 .
.
2. Этап решения математической задачи: Средствами математического анализа находится наибольшее или наименьшее значение функции на некотором промежутке.
3. Этап интерпретации найденного решения: Найденное решение «переводится» с языка математики в терминах первоначальной задачи.
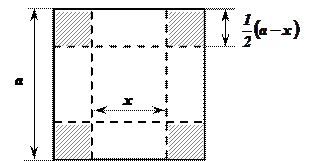
Пример: Из квадратного листа жести со стороной «а» надо изготовить открытую сверху коробку, вырезав по углам квадратики и загнув образовавшиеся кромки. Какой должна быть сторона основания коробки, чтобы ее объем был максимальным?
Решение:
х – длина стороны основания коробки;
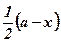 – длина стороны вырезанного квадратика;
– длина стороны вырезанного квадратика;
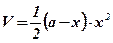 – объем коробки
– объем коробки
По смыслу задачи число х удовлетворяет неравенству 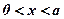 , то есть
, то есть 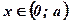 .
.
Таким образом, данная прикладная задача сведена к математической задаче:
найти наибольшее значение функции 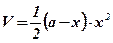 на интервале
на интервале 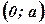 .
.
 | |||
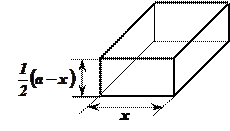 | |||
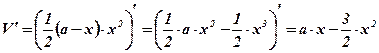 ;
;
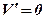 ;
; 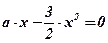 ;
; 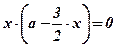 ; х = 0;
; х = 0; 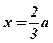 .
.
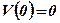 ;
; 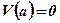 ;
; 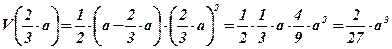 .
.
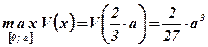 .
.
Функция 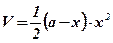 достигает своего наибольшего значения внутри отрезка
достигает своего наибольшего значения внутри отрезка 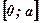 , следовательно, и внутри интервала
, следовательно, и внутри интервала 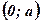 .
.
Так как х – длина стороны основания коробки, имеющей при заданных условиях максимально возможный объем, то максимальный объем, равный 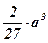 , имеет коробка со стороной основания
, имеет коробка со стороной основания 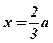 .
.
Ответ: 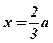 .
.
Пример: Число 36 разделить на такие две части, произведение которых давало бы наибольшее значение.
Решение:
х - первая часть числа 36; 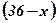 - вторая часть числа 36;
- вторая часть числа 36;
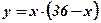 ,
, 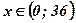 .
.
 ;
; 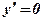 ;
; 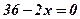 ;
; 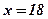 ;
;
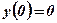 ;
; 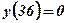 . Функция
. Функция 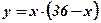 на интервале
на интервале 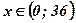 принимает положительные значения, следовательно, наибольшее значение функция принимает при
принимает положительные значения, следовательно, наибольшее значение функция принимает при 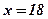 .
.
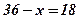 . Число 36 надо разделить на две равные части, произведение которых даст наибольшее значение.
. Число 36 надо разделить на две равные части, произведение которых даст наибольшее значение.
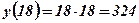 .
.
Ответ: 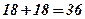 .
.
Упражнения:
Высота прямоугольного параллелепипеда и периметр его основания в сумме составляют 60 см. Основанием параллелепипеда является квадрат. Найти сторону основания и высоту параллелепипеда, чтобы его объем был наибольшим.
План исследования функции на выпуклость и существование точек перегиба
1. Найти область определения функции.
2. Вычислить первую производную функции.
3. Вычислить вторую производную функции.
4. Найти критические точки 2-ого рода функции, приравняв вторую производную функции к нулю и решив полученное уравнение.
5. Определить знак второй производной функции слева и справа от критических точек.
6. Определить характер выпуклости функции в полученных интервалах области определения функции и точки перегиба функции, если они есть.
7. Вычислить значения функции в точках перегиба.
Упражнения: Исследовать на выпуклость и существование точек перегиба функции:
1. 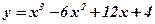 ; 2. ; 2. 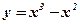 ; 3. ; 3. 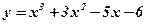 ; 4. ; 4. 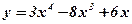 ; 5. ; 5. 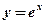 ; ; | 6. 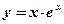 ; 7. ; 7. 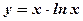 ; 8. ; 8. 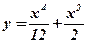 ; 9. ; 9. 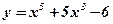 . . | 10. 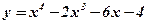 ; 11. ; 11. 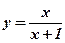 ; 12. ; 12. 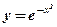 (кривая Гаусса); 13. (кривая Гаусса); 13.  Наши рекомендации
|

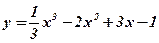 ;
;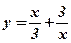 ;
;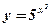 ;
;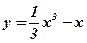 ;
;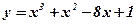 ;
;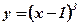 ;
;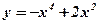 ;
;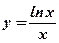 ;
;