Построение гистограммы и полигона опытного распределения случайной величины

По данным статистического ряда можно построить гистограмму и полигон распределения.

Гистограмму строят для распределений непрерывных случайных величин, а полигон – для дискретных, хотя такое правило не является обязательным.

Гистограмма распределения строится следующим образом. На оси абсцисс откладываются границы интервалов.

Из начала каждого интервала проводится ордината высотой, равной частоте для данного интервала, в принятом для оси Y масштабе. Из этой точки проводится горизонтальная линия на всю ширину интервала.

Рисунок 2.1- Гистограмма распределения износа плунжера топливного насоса высокого давления (ТНВД)

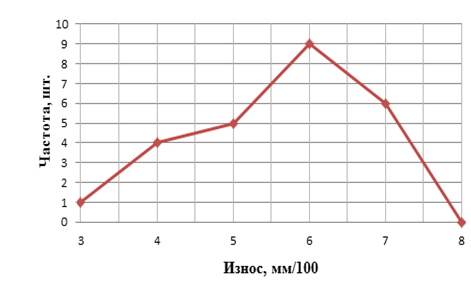
Рисунок 2.2 - Полигон распределения износа плунжера топливного насоса высокого давления (ТНВД)

Для построения полигона распределения из середины каждого интервала проводим ординату высотой, равной частоте для данного интервала. Вершины полученных ординат соединяем ломаной линией. Гистограмма и полигон распределения износов изображены на рисунке 2.1 и 2.2.

Полигон или гистограмма позволяют визуально оценить данное распределение и сделать предварительные предположения относительно вида теоретического закона распределения, подходящего к нашим опытным данным.

Выравнивание статистических рядов. Выбор теоретического закона распределения

Распределение плунжера топливного насоса высокого давления (ТНВД) (рис. 2.1) имеет явно выраженную левостороннюю асимметрию, в то время как распределение износов плунжера топливного насоса высокого давления (ТНВД) (рис. 2.2) более или менее симметрично.

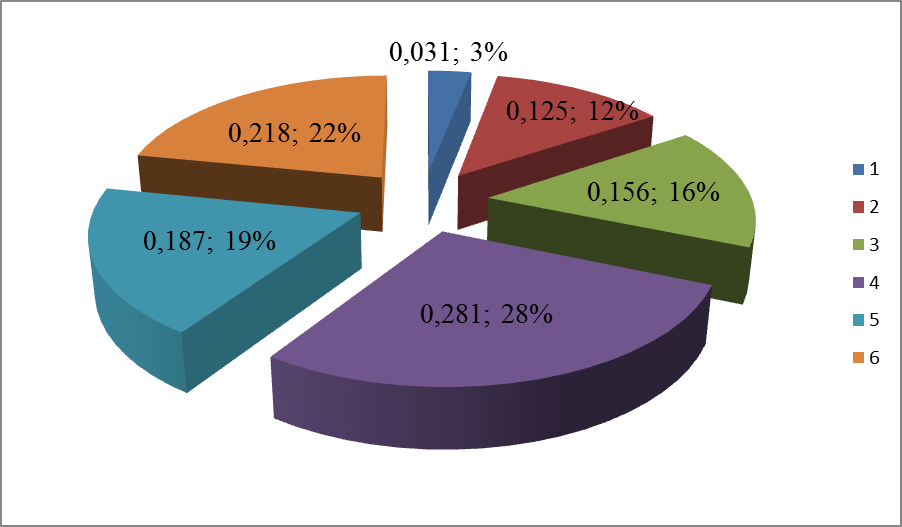
Рисунок 2.3 – Распределение опытной вероятности по данным статистического ряда износа плунжера топливного насоса высокого давления

Закон нормального распределения (ЗНР)

Формулы дифференциальной и интегральной функций для ЗНР имеют вид:

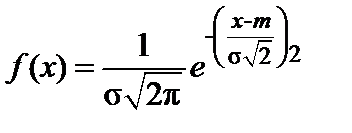, (2.2)

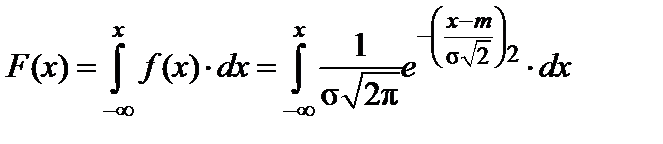. (2.3)

ЗНР – уникальный случай, когда две первые числовые характеристики совпадают с параметрами закона распределения. Поэтому параметры ЗНР для рассматриваемых примеров уже

определены и составляют:

– для износов плунжера топливного насоса высокого давления (ТНВД)

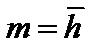= 6,1мм / 100 ≈ 0,061 мм;

Σ = 1,43 мм / 100 ≈ 0,0143 мм;

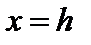(текущее значение износа);

Закон распределения Вейбулла (ЗРВ)

Формулы дифференциальной и интегральной функций для ЗРВ имеют вид:

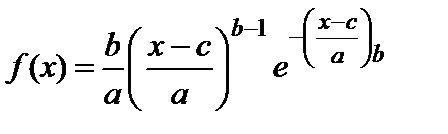, (2.4)

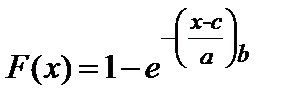, (2.5)

где а – масштабный параметр;

b – параметр формы;

с – параметр смещения (сдвига).

Следует найти вспомогательную величину V_c по формуле (2.6)

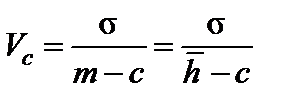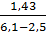= = 0,397 (2.6)

где σ – среднеквадратическое отклонение;

m – математическое ожидание ( );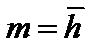

с – параметр смещения.

Находим параметр b и коэффициент К_а:

– для износов плунжера топливного насоса высокого давления (ТНВД)

b = 2,696;

К_а = 1,125;

Далее с использованием найденного коэффициента К_а находим параметр а по формуле:

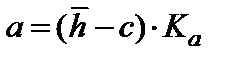. (2.7)

Для износов плунжера топливного насоса высокого давления (ТНВД)

а = (6,1-2,5)·1,125 = 4,05;

Метод разделяющих разбиений

Один из не очень точных, но зато наименее трудоемких методов нахождения оценок для параметров распределения – метод разделяющих разбиений – подробно описан в ряде источников.

Рассмотрим технику его применения на числовом примере. Требуется найти оценки параметров распределения Вейбулла с порогом чувствительности (трехпараметрическое распределение Вейбулла). Интегральная функция распределения для этого закона выражается формулой [3]:

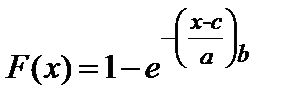, (2.8)

где х – радиальный износ гильзы, мм/100;

а – масштабный параметр;

b – параметр формы;

с – параметр смещения.

Параметр смещения с принимаем равным началу поля рассеяния, то есть, нижней границе первого интервала статистического ряда:

с = 2,5 мм/100.

Таблица 1.2.1

Радиальный износ плунжера топливного насоса высокого давления (ТНВД), мм/100

Номер интервала	Верхняя граница	То же, смещенная	Накопленная опытная вероятность
i	х	х–с	Рнакопл
	3,5		0,031
	4,5		0,156
	5,5		0,312
	6,5		0,593
	7,5		0,78
	8,5		0,99

Далее выполняем следующие шаги:

Шаг 1. Выбираем произвольно два интервала i₁ и i₂ статистического ряда. Интервалы желательно выбирать ближе к началу и концу статистического ряда, причем, i₁ < i₂. Выберем i₁ = 2 и i₂ = 5. Из соответствующих строк третьего столбца таблицы выписываем значения х₁ = 2 и х₂ = 5.

Шаг 2. Из соответствующих строк четвертого столбца таблицы выписываем значения накопленных опытных вероятностей Р₁ = 0,156 и Р₂ = 0,78.

Шаг 3. Находим параметр b по формуле [3]:

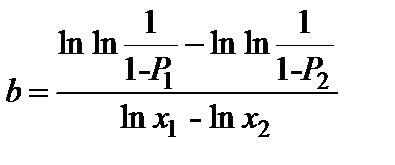. (2.9)

Подставляя выбранные нами значения х₁, х₂, Р₁ и Р₂, получаем:

b =2,35

Шаг 4. Находим параметр а:

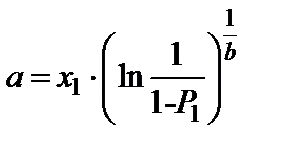(2.10)

После подстановки значений х₁ и Р₁ получаем:

а = 0,94

Искомые оценки параметров распределения ЗРВ составляют:

а = 0,94;

b = 2,35;

с = 2,5;

Для облегчения вычисления значений логарифмов и двойных логарифмов входящей в формулы (2.9) и (2.10) дроби 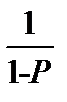приведены их значения при изменении Р в диапазоне 0,01–0,99.

Графический метод

У подавляющего большинства законов распределения график интегральной функции представляет собой кривую. Основная идея графических методов состоит в том, чтобы «выпрямить» эту кривую, то есть, подобрать для осей координат такие переменные масштабы, которые превратили бы график функции распределения в прямую линию.

В случае экспоненциального распределения это достигается созданием логарифмической шкалы на оси ординат. Для распределения Вейбулла логарифмическими шкалами снабжают и ось ординат, и ость абсцисс.

Если график снабдить соответствующими линиями сетки для обеих осей, то это позволяет легко наносить на график экспериментальные точки. Через эти точки на глаз проводится прямая, которая проходила бы как можно ближе ко всем точкам. Эта прямая и будет графиком интегральной функции в принятой системе координат.

Для нахождения параметров функции в этом случае легко применить простые приближенные методы обработки эмпирических зависимостей, такие, как метод выбранных точек, метод натянутых нитей и др. [6].

В практике обработки опытных данных при изучении случайных величин широко используется построенная по описанному принципу вероятностная бумага. Опишем технику использования вероятностной бумаги для оценки параметров распределения Вейбулла. Пусть требуется с использованием вероятностной бумаги найти оценки параметров ранее рассмотренного распределения Вейбулла для износа [3].

Вероятностная бумага для распределения Вейбулла (рис.2.4) представляет собой логарифмическую сетку. Для расширения диапазона варьирования случайной величины х подразумевается, что по оси абсцисс откладывается ее масштабированное значение, то есть произведение х·10^j, где j – целое число (порядок масштабного множителя).

В рассматриваемом примере величина х изменяется в пределах 2–12 (третий столбец табл. 1.3.3), поэтому j целесообразно принять равным нулю. Если бы износ замерялся не в сотых долях миллиметра, а в миллиметрах, то величина х варьировала бы в диапазоне 0,02–0,12. В этом случае j следовало бы принять равным 2. Аналогично, если бы х варьировала в диапазоне 20–120 единиц, то j следовало бы принять равным –1.

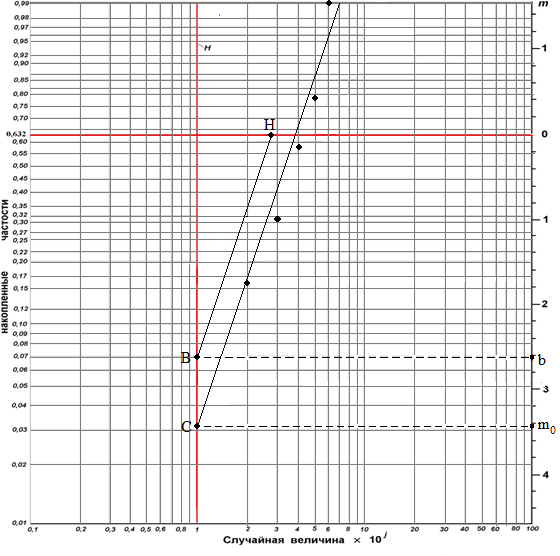
Рисунок 2.4 - Вероятностная бумага распределения Вейбулла

Таким образом, при j = 0 шкала оси абсцисс позволяет поместить величину в интервале 0,1–100, при j = 1 – в интервале 1–1000, при j = =2 – в интервале 10–10000 и т. д. Величина j может принимать и отрицательные значения. Например, при j = –1 диапазон шкалы оси абсцисс составит 0,01–10, при j = –2 – 0,001–1 и т. д.

Помимо сетки, вероятностная бумага для распределения Вейбулла снабжена двумя вспомогательными линиями и вспомогательной шкалой m, расположенной вертикально в правой части листа.

Первая вспомогательная линия (на рисунке обозначена буквой Н) является вертикалью с абсциссой, равной 1. Вторая вспомогательная линия – горизонталь с ординатой 0,632.

На этой линии отмечена точка А с абсциссой 2,718 (основание натуральных логарифмов). Эта линия определяет также нулевое значение шкалы m. Для нахождения параметров распределения следует отложить на сетке все экспериментальные точки статистического ряда, используя в качестве абсциссы третий столбец таблицы, а в качестве ординаты – четвертый (накопленные опытные вероятности). Через отложенные точки на глаз проводится прямая, проходящая на минимальном расстоянии от всех точек. Эта прямая представляет собой график интегральной функции распределения.

Для нахождения параметра b из точки А проводится прямая, параллельная функции распределения. Из точки В пересечения этой прямой со вспомогательной прямой Н проводится горизонталь до пересечения со шкалой m и по этой горизонтали со шкалы m считывается значение параметра b. В данном случае оно равно ≈ 1,73.

Точка С пересечения функции распределения со вспомогательной прямой Н используется для определения параметра а. Для этого из точки С проводят до шкалы m горизонталь и считывают на шкале m вспомогательную величину m₀. В нашем примере она получилась равной ≈ 2,93.

Параметр а находится по формуле (2.11):

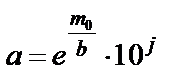, (2.11)

где m₀ – вспомогательная величина, считанная по шкале m;

b – параметр формы обрабатываемого распределения Вейбулла;

j – порядок масштабного множителя.

Подставляя в эту формулу значения из нашего примера m₀ = 3,4, b = 2,6, и j = 0, получаем

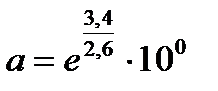= 3,7

Таким образом, найденные с использованием вероятностной бумаги параметры распределения составляют:

а = 3,7;

b = 2,6;

с = 2,5.

Как видим, совпадение с результатами применения метода разделяющих разбиений весьма хорошее. Однако, следует иметь в виду, что точность метода разделяющих разбиений существенно ниже, поскольку он из всей совокупности опытных данных использует всего лишь две экспериментальных точки. Поэтому использование вероятностной бумаги всегда предпочтительнее, хотя несколько более трудоемко.