Калиниградский государственный технический

КАЛИНИГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ

Под редакцией

Г.Г. АРУНЯНЦА

Моделирование

Экономических процессов

Курс лекций для студентов специальности: Прикладная

Информатика в экономике

Калининград 2007

СОДЕРЖАНИЕ

ВВЕДЕНИЕ. 4

Глава 1... МОДЕЛИ И МОДЕЛИРОВАНИЕ. 6

1.1. Понятие модели и моделирования. Классификация видов моделирования и моделей систем. 6

1.2. Принципы системного подхода в моделировании систем. Общая характеристика проблемы моделирования систем. 20

1.3. Основные принципы построения экономико-математических моделей 31

1.4. Математическое описание экономических систем и явлений. 36

1.5. Примеры составления математических моделей. 41

1.6. Основные разделы прикладной математики, применяемые в экономических исследованиях. 46

Глава 2... ПРОЦЕСС ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ.. 49

2.1. Определение задачи исследования. Обследование объекта и построение сценариев его функционирования. 49

2.2. Формирование концептуальной модели. 64

2.3. Построение и анализ математической модели. 83

Глава 3... МЕТОДЫ ПОИСКА РЕШЕНИЙ НА МОДЕЛЯХ.. 95

3.1. Методы поиска оптимальных решений для однокритериальных моделей с детерминированными факторами. 95

3.2. Поиск решений при наличии в модели случайных и неопределенных факторов. 101

3.3. Методы многокритериальной оптимизации. 108

Глава 4... ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ 113

4.1. Особенности и принципы построения имитационных моделей. 113

4.2. Реализация имитационных моделей на ЭВМ.. 121

4.3. Принципы оценки адекватности и точности моделей. 138

ЛИТЕРАТУРА.. 148

ВВЕДЕНИЕ

Необходимость использовать достижения научно-технического прогресса, осуществлять качественные изменения в технике и технологии при быстром обновлении продукции отраслей, решать вопросы рационального использования материалов и трудовых ресурсов, повышения эффективности работы оборудования требует повышения научной обоснованности методов управления производством. Оно необходимо еще и тем, что создание новой технологии особенно конкурентоспособной, связано с выполнением различных многовариантных исследований. В этих условиях требуется переход к широкому использованию экономико-математических методов и моделей, обеспечивающих выбор наилучшего варианта управления с точки зрения экономии ресурсов, повышения эффективности проектирования и создания современной техники. Кроме того, использование методов моделирования открывает широкие возможности для обоснованного и своевременного определения потребности в ресурсах, выполнения комплексного технико-экономического анализа деятельности объединений, предприятий и организаций, совершенствования их организационных структур управления. прогнозирования наиболее эффективных направлений их развития, специализации и кооперации. Использование на предприятиях математических методов и ЭВМ даже для решения локальных задач приносит значительный экономический эффект.

Так как наши знания, имеющаяся информация о системе, как правило, не задаются извне, а являются результатом ее непосредственного изучения, т.е. возникают при выявлении целей, задач, функций и структуры системы и их отображении в определенных языках, то уже на этом уровне объективно возникает необходимость в построении и исследовании моделей.. Именно построение и исследование моделей, а не только применение готовых моделей, как трактуют это многие авторы, составляет процесс моделирования.

В процессе построения модели необходимо принимать во внимание три основных условия: 1) насколько важную функцию системы отражает модель; 2) возможность получения необходимой информации о системе, ее надежность, полноту и объем данных; 3) пропускную способность имеющихся средств и методов сбора, хранения и обработки данных. Первое условие определяет желаемый результат, два последних – целесообразность моделирования.

На первом этапе определяется состав исследуемой сложной системы, ее структура (подсистемы) и глобальная цель, формулируются требования к информационному обеспечению системы. Здесь же формулируются цели и функции подсистем. Язык, применяемый на этом этапе, – совокупность терминов и понятий, используемых при изучении экономико-организационных вопросов производства. Поэтому модели, построенные в результате первого этапа системного моделирования, являются экономико-организационными.

На втором этапе – этапе системного экономико-математического моделирования – осуществляется процесс дальнейшей формализации моделей, доведение их до уровня, воспринимаемого вычислительной системой, разрабатывается математическое обеспечение АСУП, на основе которого уточняется лексика информационной базы. Формализация выступает здесь как процесс последовательного перевода (трансляции) моделей с экономико-организационного языка на язык формализованных экономико-математических моделей и далее на язык вычислительной системы.

Основополагающей методологией изучения данного курса является диалектический материализм. В соответствии с этим экономические процессы рассматриваются в динамике и взаимосвязи с раскрытием их внутренних противоречий, в единстве качественных и количественных изменений. Непосредственно из диалектического метода вытекает системный подход к изучению моделирующих явлений – комплексное исследование производственно-экономической системы как единого целого с позицией системного анализа.

Системный анализ – это совокупность научных методов и практических приемов решения сложных проблем (технических, экономических и т.д.). Согласно этому анализу, различные отрасли, их объединения и предприятия рассматриваются как сложные социально-экономические системы, органически связанные и активно взаимодействующие с другими отраслями и между собой в рамках единого народного хозяйства. Системный подход к организации планирования и управления требует совмещения разрозненных, частных моделей и отдельных частных вопросов в общей концепции, позволяющей видеть всю систему связей и отношений, весь комплекс параметров.

В настоящем курсе методы поиска решений для моделей различных типов не представляются подробно, а дается только их краткий обзор. В то же время большое внимание уделяется вопросам методологии моделирования с иллюстрацией теоретических положений рядом примеров. Отличительной особенностью настоящего курса от аналогичных учебных пособий является системное изложение методологических основ построения экономико-математических моделей, представление инженерного алгоритма процесса их разработки.

Глава 1.
МОДЕЛИ И МОДЕЛИРОВАНИЕ

Примеры составления математических моделей

Пример 1.5.1.

Пусть некоторый экономический регион производит несколько (n) видов продуктов исключительно своими силами и только для населения данного региона. Предполагается, что технологический процесс отработан, а спрос населения на эти товары изучен. Надо определить годовой объем выпуска продуктов, с учетом того, что этот объем должен обеспечить как конечное, так и производственное потребление.

Составим математическую модель этой задачи. По ее условию даны: виды продуктов, спрос на них и технологический процесс; требуется найти объем выпуска каждого вида продукта.

Обозначим известные величины:

c_i – спрос населения на i-й продукт (i=1,...,n); a_ij – количество i-го продукта, необходимое для выпуска единицы j -го продукта по данной технологии ( i=1,...,n ; j=1,...,n);

Обозначим неизвестные величины:

х_i – объем выпуска i-го продукта (i=1,...,n); совокупность с=( c₁ ,...,c_n ) называется вектором спроса, числа a_ij – технологическими коэффициентами, а совокупность х =( х₁ ,...,х_n ) – вектором выпуска.

По условию задачи вектор храспределяется на две части: на конечное потребление (вектор с) и на воспроизводство (вектор х-с). Вычислим ту часть вектора хкоторая идет на воспроизводство. По нашим обозначениям для производства х_j количества j-го товара идет a_ij · х_j количества i-го товара.

Тогда сумма a_i1 · х₁ +...+ a_in · х_n показывает ту величину i-го товара, которая нужна для всего выпуска х =( х₁ ,...,х_n ).

Следовательно, должно выполняться равенство:

.

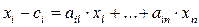Распространяя это рассуждение на все виды продуктов, приходим к искомой модели:

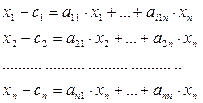
Решая эту систему из n линейных уравнений относительно х₁ ,...,х_n и найдем требуемый вектор выпуска.

Для того, чтобы написать эту модель в более компактной (векторной) форме, введем обозначения:

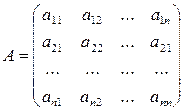
Квадратная ( 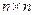) —матрица А называется технологической матрицей. Легко проверить, что наша модель теперь запишется так: х-с=Ах или

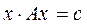(1.6)

Мы получили классическую модель «Затраты – выпуск», автором которой является известный американский экономист В. Леонтьев.

Пример 1.5.2.

Нефтеперерабатывающий завод располагает двумя сортами нефти: сортом А в количестве 10 единиц, сортом В — 15 единиц. При переработке из нефти получаются два материала: бензин (обозначим Б) и мазут (М). Имеется три варианта технологического процесса переработки:

I: 1ед.А + 2ед.В дает 3ед.Б + 2ед.М

II: 2ед.А + 1ед.В дает 1ед.Б + 5ед.М

III: 2ед.А + 2ед.В дает 1ед.Б + 2ед.М

Цена бензина — 10 долл. за единицу, мазута — 1 долл. за единицу.

Требуется определить наиболее выгодное сочетание технологических процессов переработки имеющегося количества нефти.

Перед моделированием уточним следующие моменты. Из условия задачи следует, что «выгодность» технологического процесса для завода следует понимать в смысле получения максимального дохода от реализации своей готовой продукции (бензина и мазута). В связи с этим понятно, что «выбор (принятие) решения» завода состоит в определении того, какую технологию и сколько раз применить. Очевидно, что таких возможных вариантов достаточно много.

Обозначим неизвестные величины:

х_i – количество использования i-го технологического процесса (i=1,2,3).
Остальные параметры модели (запасы сортов нефти, цены бензина и мазута) известны.

Теперь одно конкретное решение завода сводится к выбору одного вектора х=( х₁ ,х₂ ,х₃), для которого выручка завода равна (32х₁+15х₂ +12х₃) долл. Здесь 32 долл. – это доход, полученный от одного применения первого технологического процесса (10 долл. ·3ед.Б + 1 долл. ·2ед.М = 32 долл.). Аналогичный смысл имеют коэффициенты 15 и 12 для второго и третьего технологических процессов соответственно. Учет запаса нефти приводит к следующим условиям:

для сорта А: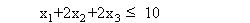

для сорта В: ,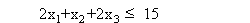

где в первом неравенстве коэффициенты 1, 2, 2 – это нормы расхода нефти сорта А для одноразового применения технологических процессов I, II, III соответственно. Коэффициенты второго неравенства имеют аналогичный смысл для нефти сорта В.

Математическая модель в целом имеет вид:

Найти такой вектор х = ( х₁ ,х₂ ,х₃), чтобы максимизировать

f(x) =32х₁+15х₂ +12х₃

при выполнении условий:

.

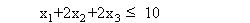
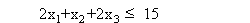
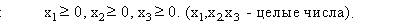Сокращенная форма этой записи такова:

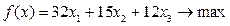
при ограничениях

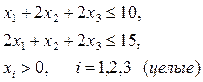(1.7)

Мы получили так называемую задачу линейного программирования.

Модель (1.7.) является примером оптимизационной модели детерминированного типа (с вполне определенными элементами).

Пример1.5.3.

Инвестору требуется определить наилучший набор из акций, облигаций и других ценных бумаг для приобретения их на некоторую сумму с целью получения определенной прибыли с минимальным риском для себя. Прибыль на каждый доллар, вложенный в ценную бумагу j - го вида, характеризуется двумя показателями: ожидаемой прибылью и фактической прибылью. Для инвестора желательно, чтобы ожидаемая прибыль на один доллар вложений была для всего набора ценных бумаг не ниже заданной величины b.

Заметим, что для правильного моделирования этой задачи от математика требуются определенные базовые знания в области портфельной теории ценных бумаг.

Обозначим известные параметры задачи:

n – число разновидностей ценных бумаг; а_j – фактическая прибыль (случайное число) от j-го вида ценной бумаги ; 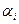– ожидаемая прибыль от j-го вида ценной бумаги.

Обозначим неизвестные величины:

y_j — средства, выделенные для приобретения ценных бумаг вида j.

По нашим обозначениям вся инвестированная сумма выражается как .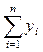
Для упрощения модели введем новые величины

.

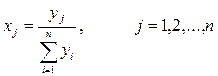Таким образом, х_i — это доля от всех средств, выделяемая для приобретения ценных бумаг вида j.

Ясно, что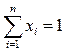

Из условия задачи видно, что цель инвестора — достижение определенного уровня прибыли с минимальным риском. Содержательно риск — это мера отклонения фактической прибыли от ожидаемой. Поэтому его можно отождествить с ковариацией 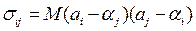прибыли для ценных бумаг вида i и вида j. Здесь М — обозначение математического ожидания.

Математическая модель исходной задачи имеет вид:

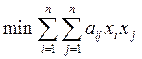
при ограничениях

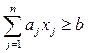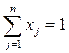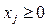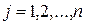, , , . (1.8)

Мы получили известную модель Марковица для оптимизации структуры портфеля ценных бумаг.

Модель (1.8.) является примеров оптимизационной модели стохастического типа (с элементами случайности).

Пример1.5.4.

На базе торговой организации имеется n типов одного из товаров ассортиментного минимума. В магазин должен быть завезен только один из типов данного товара. Требуется выбрать тот тип товара, который целесообразно завести в магазин. Если товар типа j будет пользоваться спросом, то магазин от его реализации получит прибыль р_j , если же он не будет пользоваться спросом - убыток q_j .

Перед моделированием обсудим некоторые принципиальные моменты. В данной задаче лицом, принимающим решение (ЛПР), является магазин. Однако исход (получение максимальной прибыли) зависит не только от его решения, но и от того, будет ли завезенный товар пользоваться спросом, т. е. будет ли выкуплен населением (предполагается, что по какой-то причине у магазина нет возможности изучить спрос населения). Поэтому население может рассматриваться как второе ЛПР, выбирающее тип товара согласно своего предпочтения. Наихудшим для магазина «решением» населения является: «завезенный товар не пользуется спросом». Так что, для учета всевозможных ситуаций, магазину нужно считать население своим «противником» (условно), преследующим противоположную цель – минимизировать прибыль магазина.

Итак, имеем задачу принятия решения с двумя участниками, преследующими противоположные цели. Уточним, что магазин выбирает один из типов товаров для продажи (всего n вариантов решений), а население — один из типов товаров, который пользуется наибольшим спросом (n вариантов решений).

Для составления математической модели нарисуем таблицу с n строками и n столбцами (всего n² клеток) и условимся, что строки соответствуют выбору магазина, а столбики — выбору населения. Тогда клетка (i, j) соответствует той ситуации, когда магазин выбирает i-й тип товара (i-ю строку), а население выбирает j-й тип товара (j-ю столбик). В каждую клетку запишем числовую оценку (прибыль или убыток) соответствующей ситуации с точки зрения магазина:

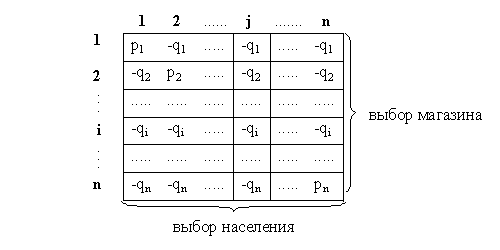
Числа q_i написаны с минусом для отражения убытка магазина; в каждой ситуации «выигрыш» населения (условно) равен «выигрышу» магазина, взятому с обратным знаком.

Сокращенный вид этой модели таков:

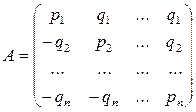(1.9)

Мы получили так называемую матричную игру. Модель (1.9.) является примером игровых моделей принятия решения.

Этап 1.

При анализе собранной информации и построения сценария функционирования объекта в первую очередь строят его каноническую модель. Для этого прежде всего выявляют границы между объектом и внешней средой (т.е. определяют понятие «исследуемый объект») и между внешней средой и окружением. Для исследуемой системы (процесса) окружение есть множество всех объектов вне системы, изменение характеристик которых влияет на систему или (и) характеристики которых изменяются вследствие поведения системы. Таким образом, окружение есть учитываемая при исследовании часть внешней среды.

Таблица 2.1. Процедура построения сценария

Этап	Содержание сценария	Результат проведения этапа: Элемент описания
	Определение понятия «объект» и «окружение». Анализ и классификация входов и выходов объекта	Каноническая модель объекта, перечень и классификация входов и выходов
	Изучение структуры объекта и его отдельных элементов	Иерархическая модель структуры объекта. Модель внутренней структуры
	Разнесение входных воздействий по элементам объекта. Описание микрообъектов– элементов и их окружения	Канонические модели для каждого из элементов объекта, перечни параметров, характеризующих отдельные элементы объекта
	Выделение элементарных процессов, происходящих в исследуемом объекте	Перечень элементарных процессов (моделей процессов, которые предстоит построить)
	Описание взаимодействия отдельных элементов объекта между собой и с окружением при возможных состояниях окружения	Функциональные модели операций, выполняемых объектом, информационные и процедурные модели

Рассмотрим особенности канонических моделей. Объект взаимодействует с окружением посредством входов и выходов.

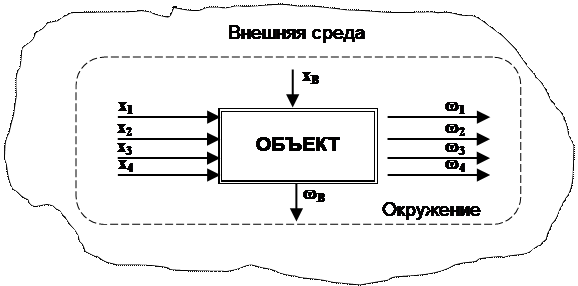
Рис. 2.1. Каноническая модель объекта исследования

Как показано на рис. 2.1. , основными типами входов являются: x₁ –информационный вход, управляющий деятельностью объекта или подлежащий переработке объектом; x₂– энергетический вход, обеспечивающий развитие объекта или его поддержание на заданном уровне производительности; x₃ – материальный вход, представляющий собой поток материальных средств, подлежащих переработке объектом либо потребляемых в процессе его функционирования; x₄ – кадровый вход, обеспечивающий объект подготовленными для участия в процессе функционирования кадрами.

Указанные входы представляют собой организованные входы, их наличие обеспечивается целеустремленной деятельностью людей. Помимо организованных входов есть неорганизованные, как правило, затрудняющие деятельность системы входы – возмущения х_В, поступающие из окружения (срывы сроков поставки материалов, несоответствие марки материала и т.д.), которые также могут быть классифицированы по этим четырем типам.

Таким образом, вход исследуемого объекта представляет собой вектор

.

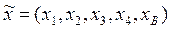Каждый вход может иметь несколько составляющих, так что

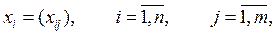
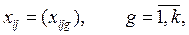
где i - тип входа; j – номенклатура входа; g – источник входа.

Результат деятельности системы – вектор выхода 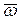может быть охарактеризован аналогичными составляющими:

,

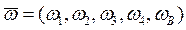где 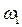– информационный выход, характеризующий результат информационной деятельности системы; 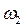– энергетический выход, характеризующий передачу энергии от системы в окружающую среду и отход элементов системы (по выработке их ресурса), несоответствию требований или дефектам; 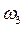– материальный выход, характеризующий материальный результат целенаправленного действия системы (то, что система произвела), а также отходы сырья и материалов; 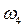– кадровый выход, характеризующий движение (выбытие) кадров; 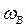–выход-возмущение, характеризующий побочные действия объекта на окружение (в свою очередь также может быть подраздел на информационный, энергетический, материальный и кадровый).

Как и для входов, составляющие вектора выхода могут быть представлены в виде

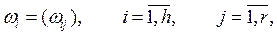
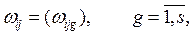
где i - тип выхода; j – номенклатура выхода; g – назначение выхода.

Характерные входы и выходы производственной системы представлены в табл. 2.2.

Таблица 2.2. Типовые входы и выходы канонической модели

Тип	Входы	Входы
Материальные	Сырье, материалы и полуфабрикаты; деньги, узлы, агрегаты, изготовляемые по планам кооперации. Технологическое оборудование и оснастка, здания и сооружения, возводимые взамен изношенных	Готовые изделия; запасные части; изделия, изготовляемые по планам кооперации; отходы сырья и материалов. Отход технологического оборудования и оснастки; отход зданий и сооружений; производственные отходы
Энергетические	Электроэнергия и горюче-смазочные вещества, необходимые для производственной деятельности	Отходы горюче-смазочных веществ и различных видов энергии
Информационные	Плановые задания на изготовление продукции; техническая и технологическая документация; информация о формировании входов; информация о результатах эксплуатации изделий	Технические описания, инструкции; паспорта на продукцию; отчетная документация; информационные связи с эксплуатирующей организацией
Кадровые	Кадры, подготовленные для работы на предприятии; кадры, требующие переподготовки и подготовки силами предприятия	Кадры, переведенные в плановом порядке; потери кадров
Возмущения	Непредвиденные изменения в технической документации на изготовление изделий, непоставка в срок материалов, временный отрыв кадров от производства и т.д.	Выпуск бракованной продукции; нарушение системы кооперированных поставок; загрязнение окружающей среды производственными отходами, недостоверная информация

Определение необходимого состава факторов, включаемых в исследование, подразумевает перечисление всех факторов, влияющих как положительно, так и отрицательно на результаты работы объекта. Определить выходные факторы обычно нетрудно. Если хорошо проработан вопрос о целях и назначении исследования, требуемые выходные характеристики почти самоочевидны. Трудности возникают при определении существенности входных факторов, т.е. того, какие входные факторы влияют на исследуемую проблему и какими из них возможно и необходимо варьировать, чтобы получить желаемое решение.

При анализе факторов целесообразно кроме классификации по типам классифицировать по их следующим признакам:

1) по возможности количественного описания:

количественные, скалярно измеряющие в определенной шкале степень проявления данного свойства. Для количественных факторов необходимо дать полное техническое описание каждого фактора по основным типам свойств – пространственных, временных, информационных, физических. Кроме того, могут быть рассмотрены также такие свойства факторов, как стационарность или нестационарность, непрерывность или дискретность по времени или величине;

порядковые, позволяющие распределить множество объектов по группам, упорядочивающим анализируемые объекты по степени проявления в них изучаемого свойства, причем каждая группа соответствует некоторой области значений количественных факторов, характеризующих данное свойство. Примером может служить фактор «квалификационный разряд» рабочего, количественными характеристиками могут служить нормативы затрат труда при выполнении тех или иных производственных операций;

классификационные (номинальные), позволяющие разбивать совокупность некоторых объектов на не поддающиеся упорядочиванию однородные по анализируемому свойству классы, например профессия работника, регламент обслуживания или режим работы оборудования.

Качественные факторы этих видов в модели задаются уровнями – условными обозначениями (номерами или индексами) групп или классов, причем для порядковых факторов номера или индексы обязательно упорядочены, а для классификационных факторов порядок их обозначений безразличен. Порядковые и классификационные факторы могут существенно влиять на облик модели: в ряде случаев для описания каждого уровня или группы уровней может потребоваться построение собственной математической модели.

Часть качественной информации на современном уровне развития науки в принципе не поддается формализации в математической модели (например, влияние настроения рабочего, общественное мнение) и поэтому не может быть включена в модель.

2) по степени определенности:

детерминированными называются факторы, значения которых для исследуемого процесса фиксированы и известны исследователю;

случайными (стохастическими) факторами называются такие, для которых известен вид закона распределения и его характеристики (например, математическое ожидание, дисперсия и т.д.), хотя каждая конкретная реализация такого фактора в исследуемом процессе не известна;

неопределенными называются факторы, для которых известна только область распределения фактора – диапазон его возможных значений. Если известно, что фактор случаен, но не известен точно закон его распределения, то он также относится к неопределенным.

Неопределенные факторы появляются из-за недостаточной изученности каких либо процессов, протекающих в окружении и либо не зависящих от деятельности людей – природные неопределенности, либо появляющихся за счет поведения людей, входящих в окружение исследуемого объекта – «противника», действующего независимо от исследователя и не преследующего его целей. Факторы первой группы при дальнейшем изучении, в том числе и с помощью специально поставленных экспериментов, могут быть переведены в разряд случайных или даже детерминированных;

3) по роли факторов в модели:

выходные характеристики окружения, являющиеся входами модели функционирования объекта. Они могу быть детерминированными (начальные условия), стохастическими и неопределенными;

переменные управления (переменные математической модели), количество которых и диапазоны их изменения устанавливаются исследователем на основе изучения возможностей заказчика по управлению объектом. В качестве переменой динамической модели может выступать независимая от исследователя переменная «время»;

процедурные действия, как правило, дискретные события, влияющие на течение процесса функционирования объекта (пуск, переключение режимов работы, останов и т.п.). Часть из них может рассматриваться как качественные дискретные переменные управления ( например, режим работы, наилучший для данной ситуации). Процедурные действия в математической модели учитываются в виде логических условий, определяющих правила их введения. Как привило, каждое конкретное процедурное действие определяет свои границы изменения количественных переменных управления;

начальные параметры объекта – детерминированные факторы, характеризующие те или иные свойства элементов объекта на момент начала моделирования;

переменные состояния являются зависимыми переменными и характеризуют свойства элементов объекта, меняющиеся в процессе протекания исследуемого процесса. Это промежуточные параметры модели, значения которых зависят от значений характеристик окружения, переменных и процедур управления, начальных параметров объекта времени;

выходные переменные характеризуют либо конечное состояние объекта в результате выполнения исследуемой операции, либо интересующие исследователя конечные результаты функционирования объекта. В первом случае в качестве выходных переменных выступают те или иные переменные состояния, во втором – либо переменные состояния, либо, что значительно чаще, выходные характеристики, произведенные от переменных состояния.

Этап 2

Одновременно с анализом входных и выходных факторов изучаются внутренняя структура объекта, принимаются решения о включении тех или иных элементов изучаемого объекта в состав его будущей модели. При этом физические границы объекта вовсе не обязаны совпадать с границами модели объекта. Так, например, при рассмотрении вопросов оперативного управления производством продукции в цехе в модель можно не включать блоки работы ряда непосредственно не влияющих на него подразделений цеха (бюро труда и заработной платы, хозяйственный персонал и вспомогательные службы), установив их характеристики на определенном фиксированном уровне.

Структура объекта рассматривается с помощью моделей двух типов: иерархической модели и модели внутренней структуры.

В иерархической модели объект расчленяется на уровни согласно принципу подчинения низших уровней высшим. В общем случае любую систему можно подразделить на подсистемы определенного ранга (Рис.2.2). В качестве верхнего нулевого уровня целесообразно рассматривать суперсистему, т.е. систему, в которую исследуемый объект входит в качестве подсистемы первого ранга. Это позволяет уточнить состав подсистем суперсистемы, связанных с исследуемым объектом и входящих в его окружение.

Обеспечивающие системы n-го ранка

Основные системы n-го ранка

Ранг системы

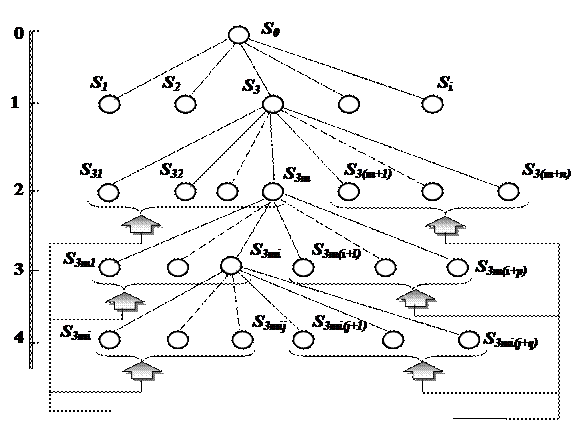
Рис. 2.2. Иерархическая модель объекта (дерево системы)

Следует отметить, что при построении иерархической модели для конкретного объекта исследования декомпозиция отдельных подсистем по уровням может проводиться с различной глубиной: степень декомпозиции будет определяться как спецификой решаемой задачи, таки имеющейся информацией об объекте.

В модели внутренней структуры отражаются взаимосвязи между элементами объекта в процессе функционирования, причем, как правило, элементы модели внутренней структуры полностью соответствуют нижним элементам иерархической модели (даже если элементы различных рангов).

Для модели внутренней структуры характерна незначительная детализация имеющихся связей. В них обычно отражаются тип связи (материальная, информационная, кадровая и т.п.) и направление связи (откуда и куда).

Для описания вида взаимосвязей можно использовать различные обозначения. В модель внутренней структуры необходимо также включать элементы окружения, что позволяет конкретизировать источники и места приложения входов и выходов в канонической модели.

Этап 3.

На этом этапе проводится детализация выявленных в структурных моделях связей. На основе решений о включении тех или иных элементов в состав модели объекта уточняются и конкретизируются назначение каждого элемента, функции, которые он выполняет в процессе работы всей системы, его входы и выходы – промежуточные параметры и переменные состояния объекта. При этом целесообразно повторить процесс построения канонических моделей для каждого из элементов модели внутренней структуры. Тем самым в модели внутренней структуры происходит как бы замещение элемента системы функциями, которые этот элемент выполняет, замещение связей между элементами связями между функциями, конкретизированные в виде переменных состояния. Затем требуется согласовать входы и выходы элементарных канонических моделей между собой и со входами и выходами канонической модели объекта в целом.

Таким образом, этап 3 является повторением этапа 1 для каждого из элементов модели внутренней структуры с обязательным согласованием всего полученного множества входов и выходов. При этом должны соблюдаться обязательные правила:

1. Выход любого элемента должен быть либо входом другого элемента, либо выходом объекта, выделенный в канонической модели.

2. Вход любого элемента должен быть либо выходом другого элемента, либо входом элемента окружения, выделенным канонической моделью.

3. Каждый вход канонической модели должен являться входом какого-либо элемента модели внутренней структуры.

4. Каждый выход канонической модели должен являться выходом какого-либо элемента модели внутренней структуры.

Однако в процессе изучения объекта эти условия подчас оказываются невыполнимыми. Это может привести к переосмысливанию канонической модели и ее корректировки, изменению состава элементов модели внутренней структуры, изменению перечней факторов, характеризующих эти элементы. Таким образом, уже на этом этапе происходит отбор информации, существенно влияющей на результаты моделирования. Информацию, описывающую те или иные стороны элемента модели внутренней структуры, но не нашедшую потребителя в рамках построенной модели, требуется временно, а может быть, и окончательно (это может показать только дальнейшая процедура построения модели) исключить из рассмотрения.

Этап 4.

Изучение места и роли каждого элемента модели внутренней структуры в процессе функционирования объекта позволяет определить перечень элементарных процессов, происходящих в исследуемом объекте, перечни функций как объекта в целом, так и каждого отдельного элемента. При выпо