Основы вероятно-статистического метода
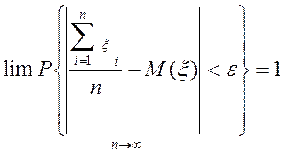Основным методом статистического моделирования является закон больших чисел. Закон больших чисел в теории вероятностей доказывает для различных условий сходимость по вероятности средних значений результатов большого числа наблюдений к некоторым постоянным величинам.
Под законом больших чисел понимают ряд теорем. Например, одна из теорем П.Л. Чебышева формулируется так: «При неограниченном увеличении числа независимых испытаний η среднее арифметическое свободных от систематических ошибок и равноточных результатов наблюдений ζi- случайной величины ζ, имеющей конечную дисперсию D(ζ), сходится по вероятности к математическому ожиданию M(ζ) этой случайной величины». Это можно записать в следующем виде:
где ε — сколь угодно малая положительная величина.
Теорема Бернулли формулируется так: «При неограниченном увеличении числа независимых испытаний в одних и тех же условиях частота Р*{А) наступления случайного события А сходится по вероятности к его вероятности Р». Согласно данной теореме для получения вероятности какого- либо события, например вероятности состояний некоторой системы Pj(t), i=0,k вычисляют частоты 
для одной реализации (испытания), далее проводят подобные вычисления для числа реализаций, равного n.
Результаты усредняют и этим самым с некоторым приближением получают искомые вероятности состояний системы. На основе вычисленных вероятностей определяют другие характеристики системы. Следует отметить, что чем больше число реализаций n, тем точнее результаты вычисления искомых величин (вероятностей состояний системы).
Решение любой задачи методом статистического моделирования состоит в следующем:
разработке и построении структурной схемы процесса, выявлении основных взаимосвязей;
формальном описании процесса;
моделировании случайных явлений (случайных событий, случайных величин, случайных функций), сопровождающих функционирование исследуемой системы;
моделировании (с использованием данных, полученных на предыдущем этапе) функционирования системы — воспроизведении процесса в соответствии с разработанной структурной схемой и формальным описанием;
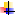накоплении результатов моделирования, их статистической обработке, анализе и обобщении.
В отличие от описанных ранее математических моделей, результаты которых
отражали устойчивое во времени поведение системы, результаты, получаемые при
статистическом моделировании, подвержены экспериментальным ошибкам. Это означает,
что любое утверждение, касающееся характеристик моделируемой системы, должно
основываться на результатах соответствующих статистических проверок.
Экспериментальные ошибки при статистическом моделировании в значительной
степени зависят от точности моделирования случайных явлений, сопровождающих
функционирование исследуемой системы.
Известно, что при изучении вероятностных систем случайные явления могут
интерпретироваться в виде случайных событий, случайных величин и случайных
функций. Следовательно, моделирование случайных явлений сводится к моделированию
случайных событий, случайных величин и случайных функций. Так как случайные
события и случайные функции могут быть представлены через случайные величины, то и
моделирование случайных событий и случайных функций производится с помощью
случайных величин. В связи с этим рассмотрим сначала способы моделирования
случайных величин.
6. Моделирование случайных величин.
Для моделирования случайной величины необходимо знать ее закон распределения.
Наиболее общим способом получения последовательности случайных чисел, распределенных по произвольному закону, является способ, в основе которого лежит их формирование из исходной последовательности случайных чисел, распределенных в интервале [0,1] по равномерному закону Равномерно распределенные в интервале [0,1] последовательности случайных чисел можно получить тремя способами:
• использованием таблиц случайных чисел;
• применением генераторов случайных чисел;
• методом псевдослучайных чисел.
При решении задачи без применения ЭВМ чаще всего используют таблицы случайных чисел. В таблицах случайных чисел случайные цифры имитируют значения дискретной случайной величины с равномерным распределением.
Недостатки данного способа полунения случайных чисел следующие:
1) трудно проверить качество вырабатываемых чисел;
2) случайные числа не воспроизводимы (если их не запоминать), и, как следствие, нельзя повторить расчет на ЭВМ для исключения случайного сбоя.
Получение псевдослучайных чисел с равномерным законом распределения заключается в выработке псевдослучайных чисел. Псевдослучайные числа - это числа, полученные по какой-либо формуле и имитирующие значения случайной величины.
Под словом «имитирующие» подразумевается, что эти числа удовлетворяют ряду тестов так, как если бы они были значениями этой случайной величины. Первый алгоритм для получения псевдослучайных чисел предложил Дж. Нейман. Это так называемый метод середины квадратов, который заключается в следующем:
Алгоритм не оправдал себя. Сейчас разрабатывается множество алгоритмов для получения псевдослучайных чисел.
Назовем достоинства метода псевдослучайных чисел.
1. На получение каждого случайного числа затрачивается несколько простых операций, так что скорость генерирования случайных чисел имеет тот же порядок, что и скорость работы ЭВМ.
2. Малый объем памяти ЭВМ цдя программирования.
3. Любое из чисел легко воспроизвести.
4. Качество генерируемых случайных чисел достаточно проверить один раз.
Подавляющее число расчетов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел. От последовательности случайных чисел, равномерно распределенных в интервале [0,1], нетрудно перейти к последовательности случайных чисел с произвольно заданным законом распределения. Существует основное соотношение, связывающее случайные
числа с заданным законом распределения и случайные числа с равномерным законом распределения в интервале [0,1]. Суть его состоит в том, что для преобразования последовательности случайных чисел с равномерным законом распределения в интервале [0,1] в последовательность случайных чисел с заданной функцией распределения F{x) необходимо из совокупности случайных чисел с равномерным законом распределения в интервале [0,1] выбрать случайное число Ъ, и решить уравнение: F{x) = I относительно х. Решение уравнения представляет собой случайное число из совокупности случайных чисел, имеющих функцию распределения F{x), В случае когда вместо функции распределения F(x) задана плотность вероятностных, соотношение (4.5) принимает вид:
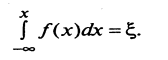
4.6
Для ряда законов распределения, наиболее часто встречающихся в реальной экономике, получено аналитическое решение уравнения (4.6), результаты которого приведены в табл. 6.1.
Моделирование случайных событий. Моделирование случайного события заключается в воспроизведении факта появления или непоявления случайного события в соответствии с заданной его вероятностью. Моделирование полной группы несовместных событий А1, А2, ..., А^, вероятности которых P(AD = Pf, / = 1, л известны, можно свести к моделированию дискретной случайной величины У, имеющей закон распределения
где вероятности ее возможных значений
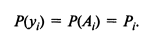
Очевидно, что принятие в испытании дискретной случайной величиной У возможного значения у^ равносильно появлению в испытании события Aj. При практической реализации данного способа на единичном отрезке числовой оси откладывают интервалы Δi= Pi (рис. 2).
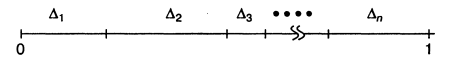
Рис.2
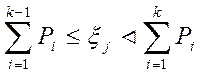Вырабатывают равномерно распределенное на интервале [0,1] случайное число ξi и проверяют условие (4.10)
Понятие о моделировании случайных функций. Для моделирования случайных функций используют два способа. В первом из них применяются специальные физические датчики, вырабатывающие непрерывные реализации случайной функции. Физические датчики
с помощью специальных фильтров преобразуют собственные шумы в случайные функции с заданными характеристиками. В основе второго способа моделирования случайных функций лежит использование случайных чисел. При этом получают значения реализации моделируемой случайной функции в изолированных точках.
Сущность способа состоит в том, что воспроизведение реализации случайной функции сводится к моделированию системы коррелированных случайных величин.
Пример.
Разыграть 8 значений дискретной случайной величины Х, закон распределения
которой задан в виде таблицы:
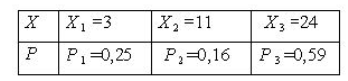
Решение
1. Разобьем интервал (0,1) оси Оr точками с координатами 0,25; 0,25+0,16=0,41 на
три частичных интервала;
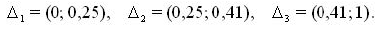
2. Выпишем из таблицы случайных чисел 9 чисел, например 0,10; 0,37; 0,08; 0,99;
0,12; 0,66; 0,31; 0,85.
3. Случайное число r1 = 0,10 принадлежит первому частичному интервалу, поэтому
разыгрываемая случайная величина приняла возможное значение x1 = 3.
Случайное число r2= 0,37 принадлежит второму частичному интервалу, поэтому
разыгрываемая величина приняла возможное значение x2 = 11. Аналогично
получим остальные возможные значения дискретной случайной величины Х.
Итак: разыгранные возможные значения Х таковы: 3; 11; 3; 24; 3; 24; 11; 24.
Как видим, можно получить множество значений случайной величины Х с
заданным законом распределения.