Кинематический анализ сооружений
Определим несколько базовых понятий, связанных с кинематическим анализом конструкций.
Введем понятие кинематической цепи. Кинематической цепью называется система дисков, соединенных между собой с помощью кинематических связей. Под диском подразумевается любое неизменяемое тело, а кинематической связью называется устройство, уничтожающее одну степень свободы, или, иначе говоря, препятствующее перемещению в одном каком-либо направлении. Степенью свободы кинематической цепи называется количество независимых геометрических параметров, определяющих положение ее элементов. Любой диск имеет в пространстве шесть, а на плоскости — три степени свободы. Например, положение твердого тела, показанного на рис.1.8,а, однозначно определяется тремя координатами точки А и тремя углами наклона прямой АВ к координатным осям. Положение плоской фигуры, показанной на рис.1.8,б, можно задать тремя параметрами: двумя координатами точки А и углом наклона прямой АВ к одной из координатных осей.
а б
Рис.1.8. К определению положения твердого тела:
А - в пространстве; б - и на плоскости
Как уже отмечалось выше, в качестве несущих конструкций могут использоваться только неизменяемые системы. Поэтому при проектировании конструкции необходимо в первую очередь выяснить, является она изменяемой или нет. Полезно также установить, является конструкция статически определимой или статически неопределимой. Напомним, что статически определимой является такая конструкция, которая может быть рассчитана с помощью одних лишь уравнений статики. Расчет статически неопределимых систем более сложен и требует применения, наряду с уравнениями равновесия, и других соотношений.
Установить неизменяемость системы можно с помощью характеристики, названной выше степенью свободы. Степень свободы показывает, по какому количеству направлений могут происходить перемещения при отсутствии деформаций. Следовательно, для кинематического анализа конструкции необходимо мысленно представить, что входящие в ее состав элементы и связи между ними являются абсолютно жесткими, и подсчитать степень свободы полученной системы. Если степень свободы конструкции с жесткими элементами равна нулю или меньше нуля, то перемещения без деформаций невозможны, и, следовательно, данная конструкция неизменяема.
Обозначим через Д число дисков системы, а через С – число кинематических связей. Тогда степень свободы плоской кинематической цепи может быть найдена по формуле:
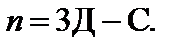 (1.1)
(1.1)
Степень свободы пространственной кинематической цепи может быть найдена так:
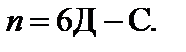 | (1.2) |
Условие неизменяемости для плоской системы имеет вид:
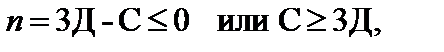 | (1.3) |
а для пространственной:
 | (1.4) |
Если для плоской системы соблюдается соотношение:
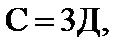 | (1.5) |
а для пространственной:
 | (1.6) |
то это означает, что конструкция является статически определимой, так как для плоской системы можно составить 3Д, а для пространственной — 6Д уравнений равновесия, из которых и можно найти усилия в С кинематических связях. Таким образом, соотношения (1.5) и (1.6) являются условиями статической определимости и геометрической неизменяемости одновременно.
Если конструкция не связана с основанием (землей), то следует говорить о внутренней ее неизменяемости. В этом случае от общего числа степеней свободы следует отнять число степеней свободы, связанных с движением конструкции как твердого тела (с движением, при котором не происходит изменения взаимного положения точек системы). Формулы для определения числа внутренних степеней свободы плоских и пространственных конструкций на основании (1.1), (1.2) и сказанного выше принимают вид:
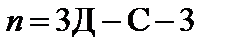 | (1.7) |
и
 | (1.8) |
соответственно.
Плоская система, не связанная с землей, является статически определимой и геометрически неизменяемой, если соблюдается условие:
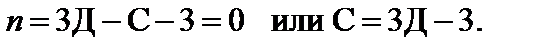 | (1.9) |
Для пространственной системы это условие принимает вид:
 | (1.10) |
Покажем, что соотношения (1.5), (1.6), (1.9) и (1.10) являются необходимыми, но недостаточными условиями статической определимости и геометрической неизменяемости. Рассмотрим, например, конструкцию, состоящую из двух стержней, соединенных между собой при помощи шарнира в точке В и имеющую одну шарнирно-неподвижную и две шарнирно-подвижные опоры (рис.1.9). Отметим, что присоединение одного диска к другому при помощи шарнира устраняет две степени свободы присоединяемого диска, так как препятствует его поступательному перемещению.
Рис.1.9. К обоснованию необходимости кинематического анализа
Очевидно, что эта конструкция является изменяемой, так как консоль ВС может свободно поворачиваться вокруг точки В. Вычислим степень свободы конструкции по формуле (1.1). Конструкция содержит два диска и имеет шесть связей — четыре внешних и две внутренних. Получаем:
 . . |
Таким образом, согласно формуле (1.1), конструкция, изображенная на рис.1.9, геометрически неизменяема, что противоречит очевидному факту ее изменяемости. Это противоречие объясняется тем, что конструкция имеет одну избыточную связь в части АВ при отсутствии одной необходимой для обеспечения неизменяемости связи в части ВС. Если переставить одну из шарнирно-подвижных опор, как показано на рис.1.10, то конструкция станет неизменяемой. Следовательно, наряду с исследованием неизменяемости по формулам (1.1—1.10), необходим кинематический анализ конструкций. В связи с этим приведем некоторые правила образования неизменяемых систем.
Рис.1.10. Пример неизменяемой системы
Предварительно рассмотрим способ соединения элементов, приводящий к так называемой мгновенной изменяемости. Пусть три диска соединены между собой с помощью шарниров, как показано на рис.1.11. Разъединим мысленно диски 1 и 2 в точке В. Диск 1 сможет поворачиваться вокруг точки А, и при этом точка В будет перемещаться по дуге окружности 1. Диск 2 сможет поворачиваться вокруг точки С, и при этом точка В будет перемещаться по дуге окружности 2. Но окружности 1 и 2 имеют общую касательную в точке В. Следовательно, в заданной системе диск 2 не препятствует бесконечно малому перемещению точки В в направлении касательной за счет вращения диска 1, а диск 1, в свою очередь, не препятствует бесконечно малому перемещению точки В направлении касательной за счет вращения диска 2.
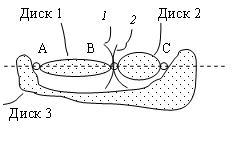
Рис.1.11. Соединение трех дисков с помощью шарниров, лежащих на одной прямой
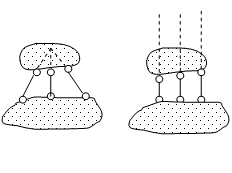
а б
Рис.1.12. Соединение двух дисков с помощью трех стержней:
а- пересекающихся в одной точке, б – параллельных друг другу
Таким образом, в системе, изображенной на рис.1.11, возможны бесконечно малые перемещения без деформации дисков. Такие системы называются мгновенно изменяемыми. Аналогичная ситуация возникает при соединении двух дисков с помощью трех стержней, пересекающихся в одной точке (рис.1.12, а). Частным случаем такого соединения является соединений с помощью трех параллельных стержней (рис.1.12, б).
Использование мгновенно изменяемых систем в качестве несущих конструкций недопустимо, так как в них могут возникать очень большие усилия (теоретически бесконечно большие) при весьма незначительных нагрузках.
Рассмотрим теперь правила образования неизменяемых систем.
1. Присоединение шарнирного узла к неизменяемой системе (диску).
Для образования неизменяемой системы шарнирный узел должен быть присоединен к диску с помощью двух стержней, оси которых не совпадают. Такой способ присоединения к диску показан на рис.1.13, а. Если оси АВ и АС совпадут, образуется мгновенно изменяемая система (три шарнира на одной прямой). Если в качестве диска использовать стержень, получится шарнирный треугольник (рис.1.13, б). Следовательно, шарнирный треугольник неизменяем.
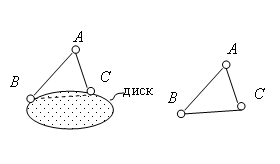
а б
Рис.1.13. Присоединение шарнирного узла к неизменяемой системе:
а ) неизменяемая система – произвольный диск; б) неизменяемая система - стержень
2. Соединение двух дисков.
Два диска образуют неизменяемую систему, если:
а) они соединены между собой тремя стержнями, осевые линии которых не параллельны друг другу и не пересекаются в одной точке;
б) они соединены между собой при помощи шарнира и стержня, осевая линия которого не проходит через этот шарнир.
Соединение двух дисков по способу а показано на рис.1.14. Если бы стержни 1,2 и 3 пересекались в одной точке (как показано на рис.1.14,б), то возможно было бы вращение дисков вокруг мгновенного центра вращения m. В схеме рис.1.14,а при отсутствии стержня 3 было бы возможно вращение дисков относительно точки пересечения m стержней 1 и 2. Стержень 3 препятствует такому вращению, если его ось не проходит через точку m. Таким образом, схема рис.1.14,а является неизменяемой, а схема рис.1.14,б — мгновенно изменяемой.


а б
Рис.1.14. Соединение двух дисков с помощью трех стержней 1, 2 и 3: а – не пересекающихся в одной точке; б – пересекающихся в одной точке

Рис.1.15. Соединение двух дисков с помощью шарнира и стержня
Соединение по способу б показано на рис.1.15. Такое соединение можно рассматривать как частный случай соединения по способу а. Доказательство неизменяемости аналогично предыдущему случаю.
3. Соединение трех дисков.
Три диска образуют неизменяемую систему, если:
а) они соединены при помощи трех шарниров, не лежащих на одной прямой;
б) они соединены при помощи шести стержней таким образом, что между каждой парой дисков имеется по два стержня, точки пересечений осей которых не лежат на одной прямой.
Соединение по схеме апоказано на рис.1.16,а, а по схеме б— на рис.1.16,б.
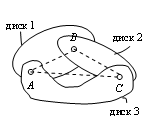
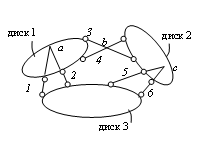
а б
Рис.1.16. Соединение трех дисков: а – с помощью трех шарниров А, В и С; б – с помощью шести стержней 1÷6, попарно пересекающихся в точках a,b иc
Если каждый из дисков, показанных на рис.1.16,а, заменить эквивалентным стержнем (пунктирные линии на этом рисунке), то получится шарнирный треугольник, неизменяемость которого была доказана выше. В схеме рис.1.16, б каждую пару стержней можно заменить фиктивным шарниром, лежащим на пересечении этих стержней. Следовательно, схема рис.1.16, б будет неизменяемой, если точки a, b, c не будут лежать на одной прямой. В противном случае система будет мгновенно изменяемой.
