Тема 5 Неопределенный интеграл
Функция 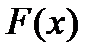 называется первообразной функции
называется первообразной функции 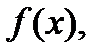 если
если 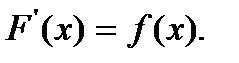 Множество первообразных функции
Множество первообразных функции 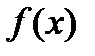 называется неопределенным интегралом и обозначается
называется неопределенным интегралом и обозначается 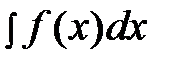 .
.
Операции дифференцирования и интегрирования взаимнообратны:
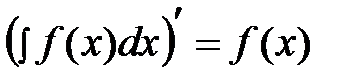 ,
,
поэтому нетрудно получить следующую таблицу интегралов:
1) 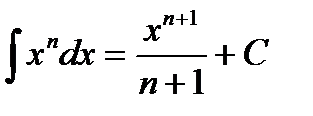 (
( 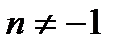 ), 7)
), 7) 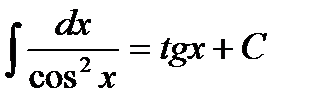 ,
,
2) 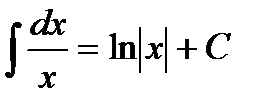 , 8)
, 8) 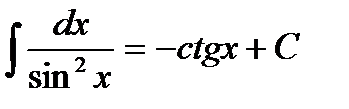 ,
,
3) 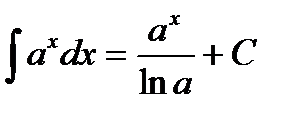 , 9)
, 9) 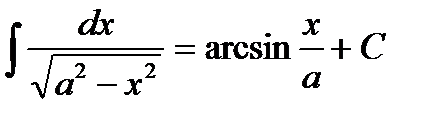 ,
,
4) 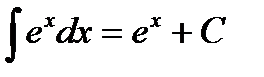 , 10)
, 10) 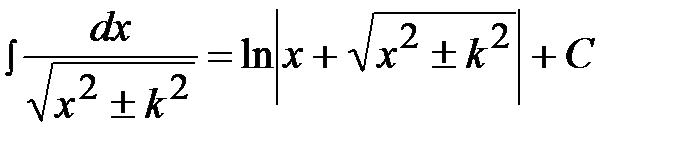 ,
,
5) 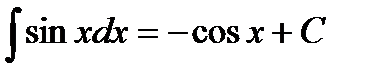 , 11)
, 11) 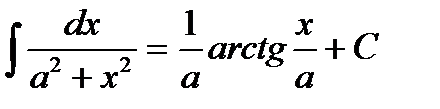 ,
,
6) 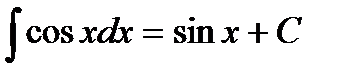 , 12)
, 12) 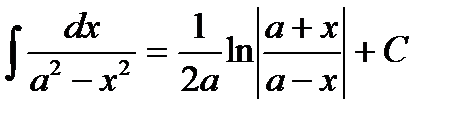 .
.
Не останавливаясь на непосредственном интегрировании по формулам, как на простейшем способе решения примеров, перейдём сразу к более сложным методам.
5.1 Метод замены переменного
Пусть требуется найти неопределенный интеграл от непрерывной функции 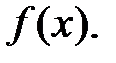
Рассмотрим некоторую функцию 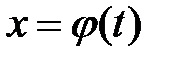 , которая имеет непрерывную производную
, которая имеет непрерывную производную 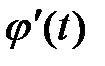 и обратную функцию
и обратную функцию 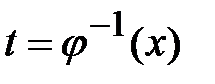 . (Например:
. (Например: 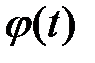 монотонна). Тогда справедлива формула:
монотонна). Тогда справедлива формула:
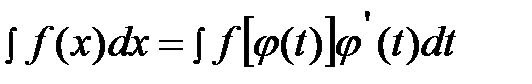 . (1)
. (1)
В некоторых ситуациях удается подобрать функцию 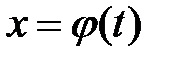 так, что интеграл в правой части (1) оказывается проще, чем в левой части. Такой прием называется методом замены переменной. На практике часто формулу используют в обратную сторону:
так, что интеграл в правой части (1) оказывается проще, чем в левой части. Такой прием называется методом замены переменной. На практике часто формулу используют в обратную сторону:
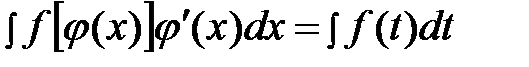 . (2)
. (2)
Другими словами, если подынтегральное выражение может быть записано в форме левой части (2), то с помощью подстановки 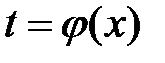 получаем более простой интеграл (1).
получаем более простой интеграл (1).
Задача 1. 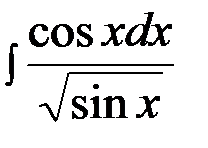 .
.
Решение.
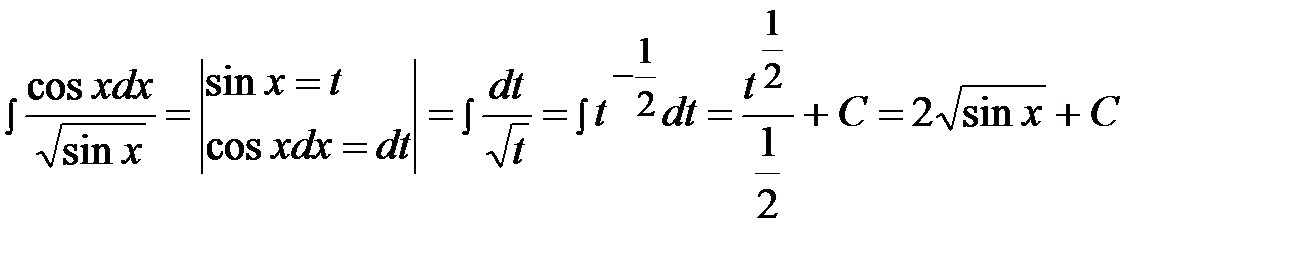 .
.
Задача 2. 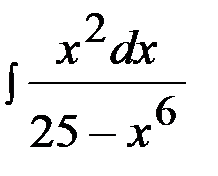 .
.
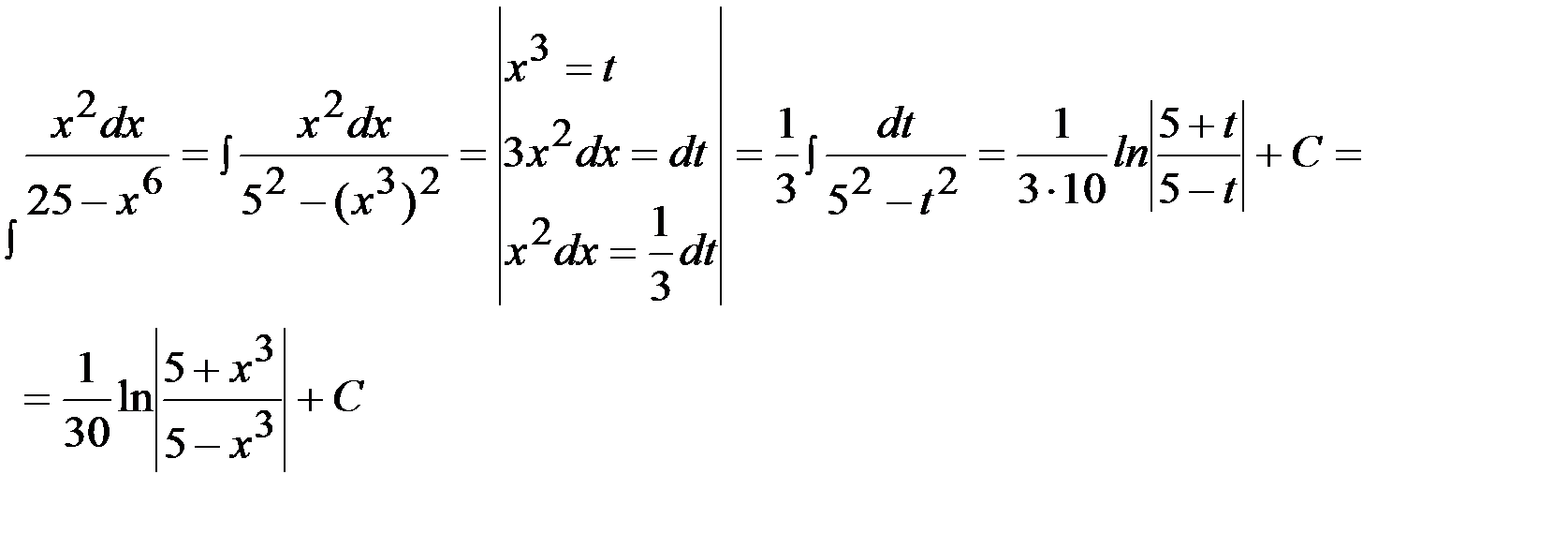
На практике часто используется следующая простая формула:
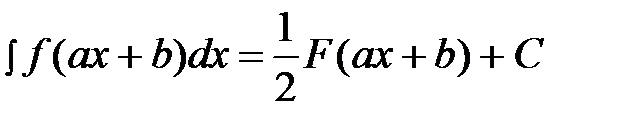 ,
,
где 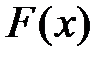 - первообразная функции
- первообразная функции 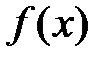 .
.
5.2 Интегрирование по частям
Формула интегрирования получается почленным интегрированием формулы производной произведения.
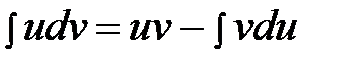 .
.
Смысл формулы заключается в том, что производная перебрасывается с одного множителя не другой и интеграл при этом может оказаться проще, чем исходный.
Можно выделить по крайней мере два класса интегралов, для которых применима формула интегрирования по частям.
I. 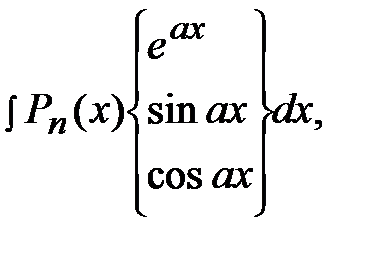
где 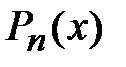 - многочлен степени
- многочлен степени 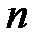 . В качестве
. В качестве 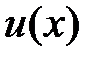 нужно взять
нужно взять 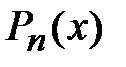 , а
, а 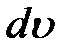 =
= 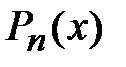 - другой сомножитель.
- другой сомножитель.
При этом формулу приходится применить столько раз, какова степень многочлена.
II. 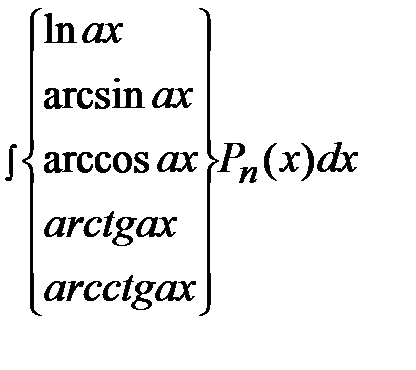 .
.
В этом случае, наоборот, следует положить 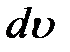 =
= 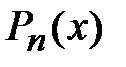 .
.
Рассмотрим применение указанной схемы.
Задача 3.
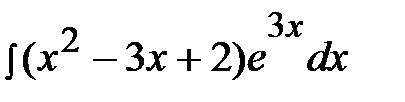 .
.
Это интеграл первого типа, поэтому:
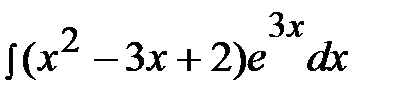 =
= 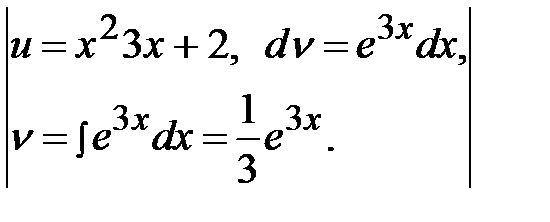 =
=
= 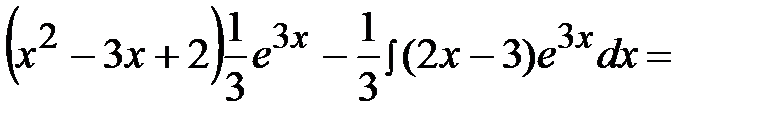
 =
=
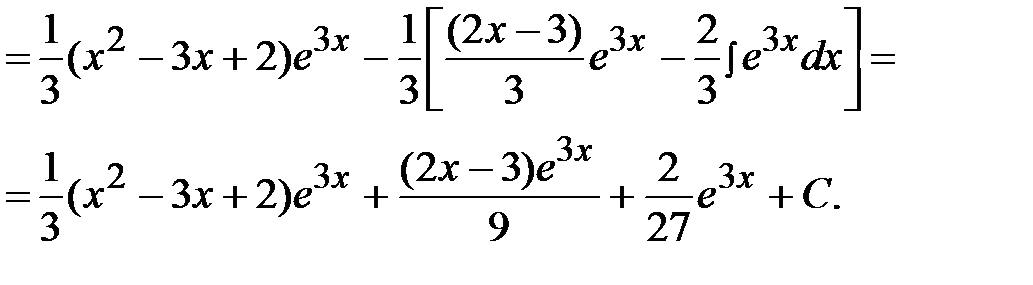
Задача 4. 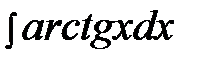 .
.
Это интеграл второго типа, поэтому имеем:
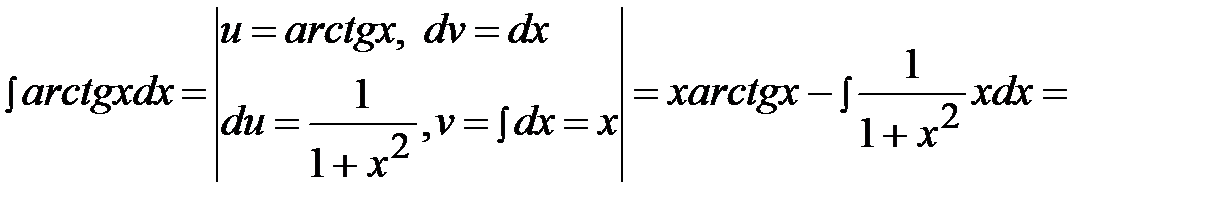
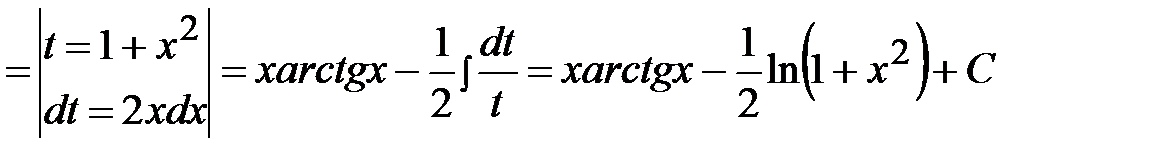 .
.
Заметим, что при использовании формулы интегрирования по частям приходится восстанавливать функцию 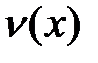 по ее дифференциалу
по ее дифференциалу 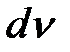 . Поэтому в качестве этого сомножителя нужно брать легко интегрируемую функцию.
. Поэтому в качестве этого сомножителя нужно брать легко интегрируемую функцию.
Формула интегрирования по частям может хорошо сработать и в других случаях.
Задача 5. 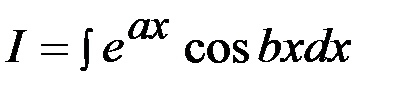 .
.
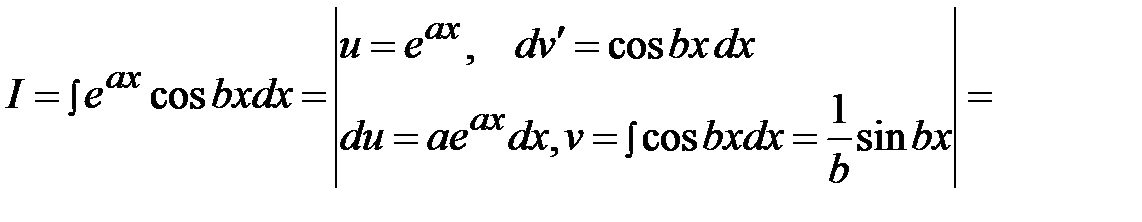
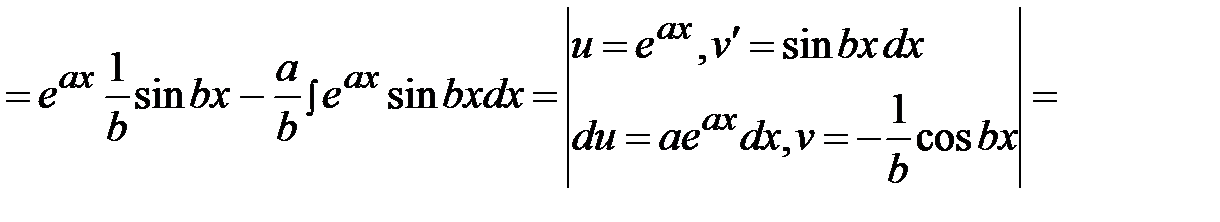
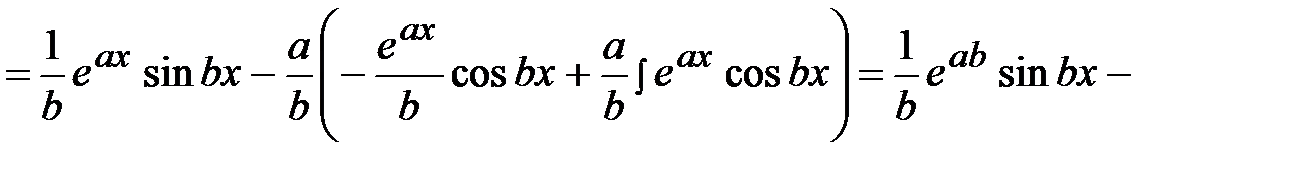
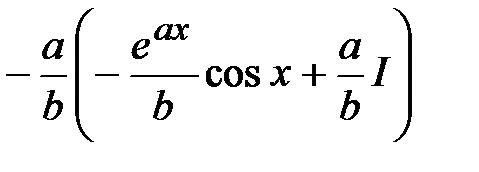 .
.
Получили уравнение относительного исходного интеграла I. Вынося I за скобки, получим
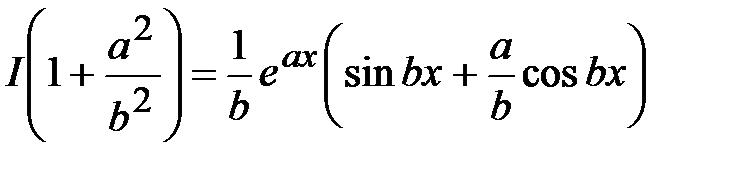 ,
,
откуда
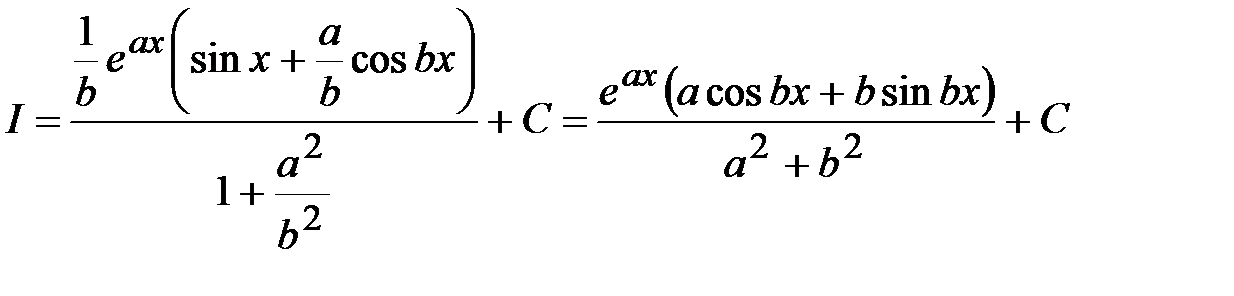 .
.
5.3 Интегрирование выражений, содержащих квадратный трехчлен
К этому типу интегралов относятся интегралы вида:
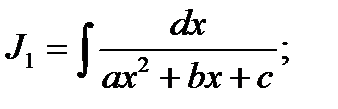
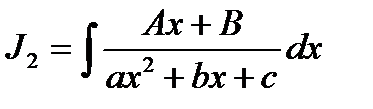 ;
;
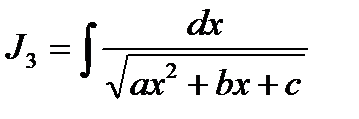 ;
; 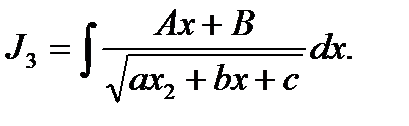
Мы увидим в дальнейшем, что без умения находить такие интегралы, мы не сможем вычислять интегралы от рациональных дробей.
Сначала научимся находить более простые интегралы видов 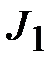 и
и 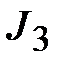 .Трудность заключается в наличии слагаемого bx. Если бы его не было, то, вынося за знак интеграла
.Трудность заключается в наличии слагаемого bx. Если бы его не было, то, вынося за знак интеграла 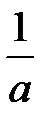 , получили бы интеграл вида (11) или (12). Решить проблему можно выделением полного квадрата.
, получили бы интеграл вида (11) или (12). Решить проблему можно выделением полного квадрата.
Задача 6. 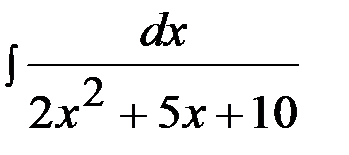 .
.
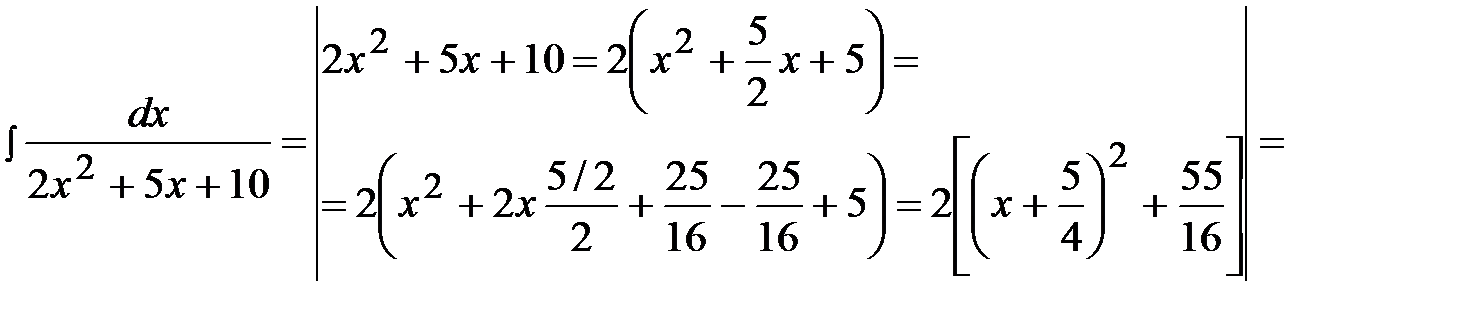
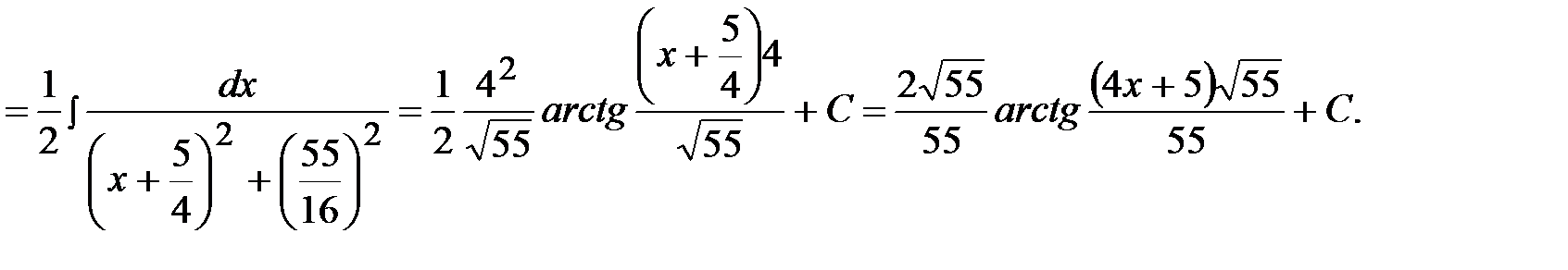
Задача 7. 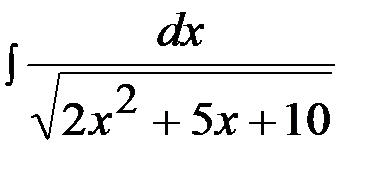 .
.
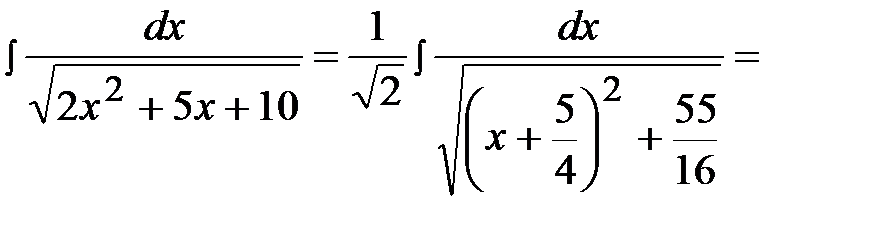
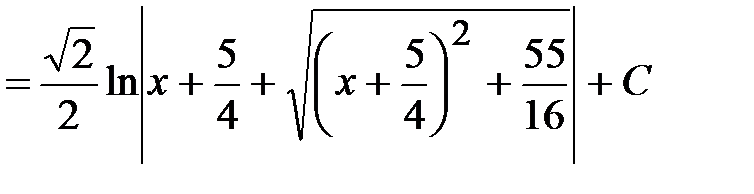
Задача 8. 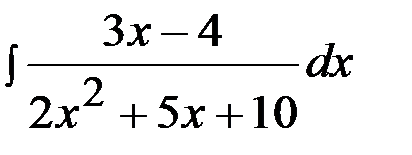 .
.
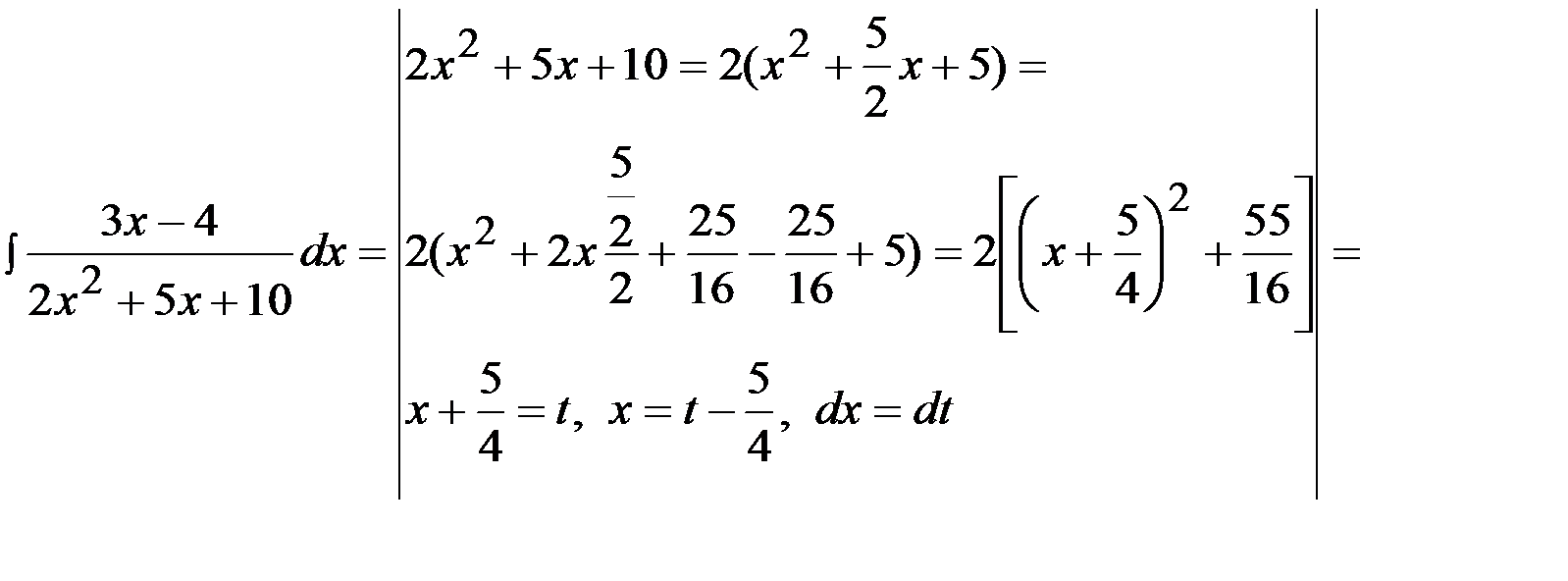
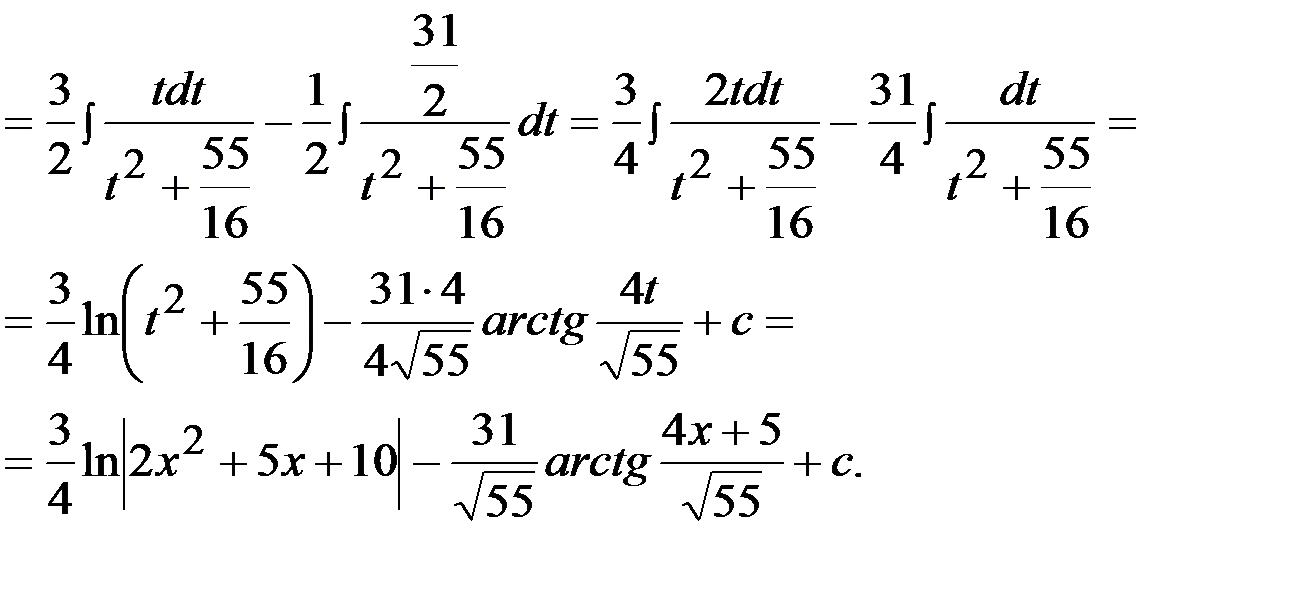
Задача 9. 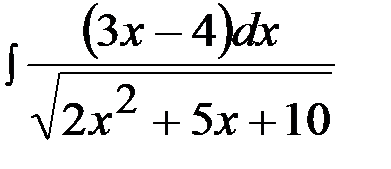 .
.
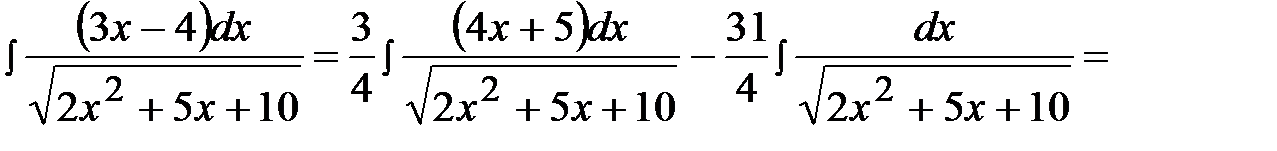
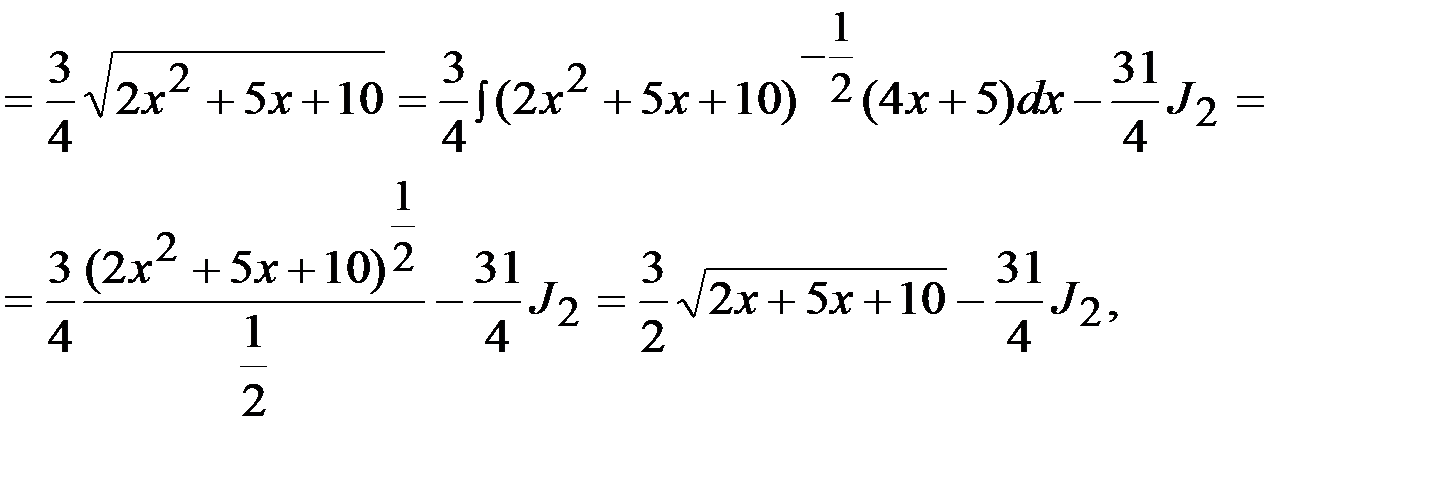
где 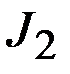 - интеграл, рассмотренный в примере 7.
- интеграл, рассмотренный в примере 7.
5.4 Интегрирование рациональных дробей
Методика интегрирования правильных дробей основана на представлении знаменателя в виде произведения линейных выражений (возможно в целых положительных степенях) и квадратичных сомножителей с отрицательными дискриминантами (возможно в целых степенях). Известен алгебраический результат, что такое представление всегда возможно.
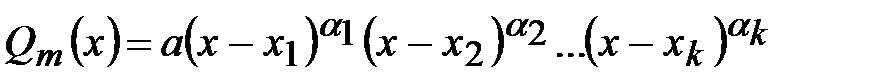
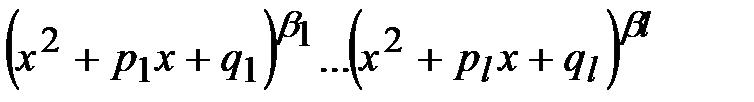 .
.
Вообще говоря, получение такого представления для многочленов высоких степеней является сложной задачей. Мы в дальнейшем будем считать, что знаменатель уже представлен в таком виде. Известен алгебраический результат, что любая правильная дробь может быть представлена в виде суммы простейших дробей, интегралы от которых легко находятся. При этом каждому линейному сомножителю вида 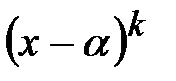 в знаменателе соответствует группа простейших дробей вида:
в знаменателе соответствует группа простейших дробей вида:
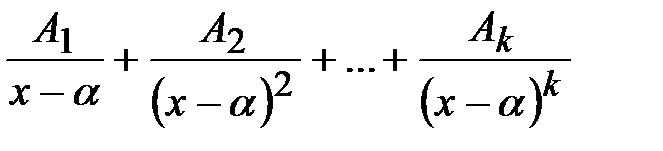 .
.
В частности при 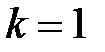 имеем только одно слагаемое:
имеем только одно слагаемое: 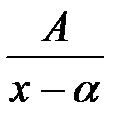 .
.
Каждому квадратичному сомножителю 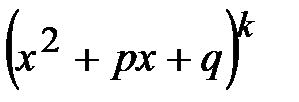 соответствует группа дробей вида:
соответствует группа дробей вида:
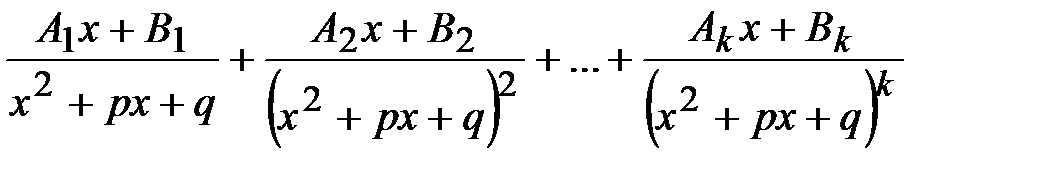 ,
,
а при 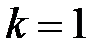 - одно слагаемое
- одно слагаемое 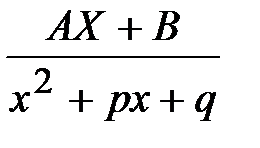 .
.
Рассмотрим примеры разложения правильной дроби на простейшие:
Задача 10. 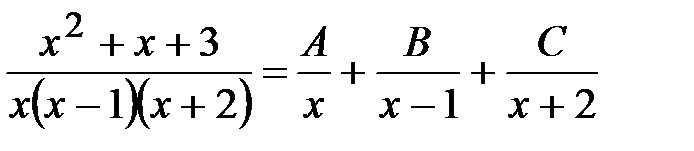 .
.
Задача 11. 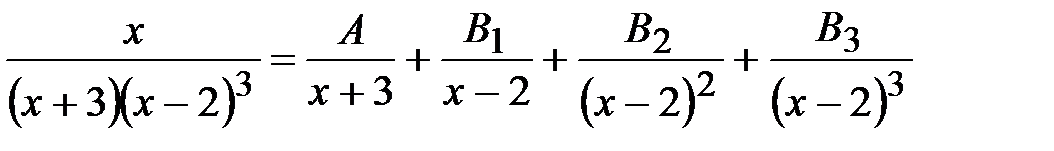 .
.
Задача 12. 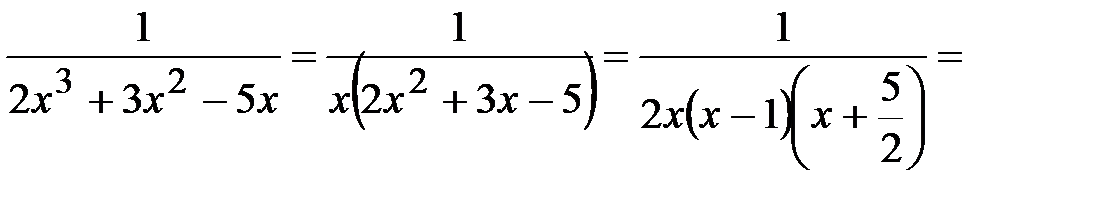
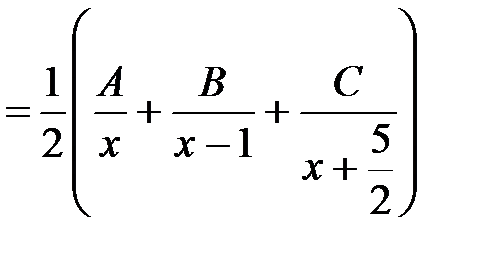 .
.
Задача 13. 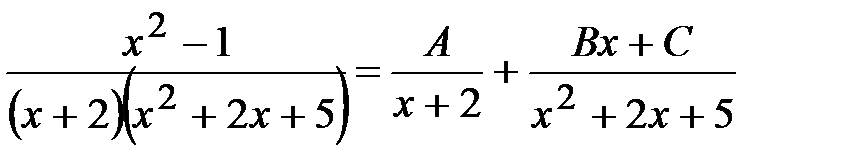 .
.
Задача 14. 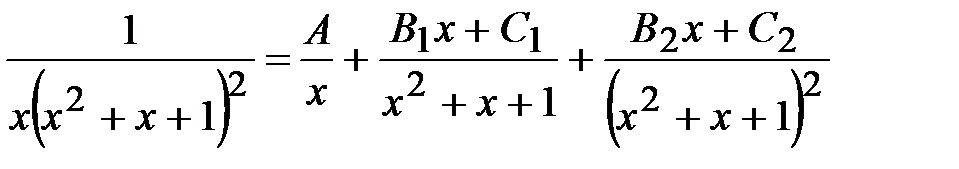 .
.
Теоретически гарантируется, что все выписанные разложения справедливы. Остается научиться находить постоянные А, В, С … . Предположим, что указанные константы найдены. Тогда интегрирование правильной дроби сведется к нахождению интегралов вида:
I 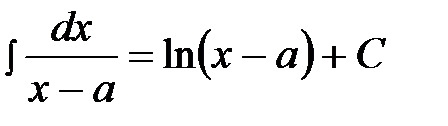 , III
, III 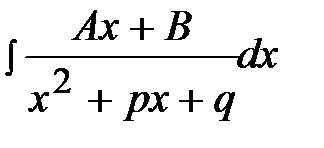 ,
,
II 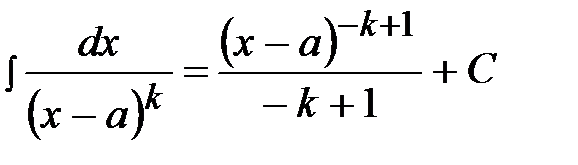
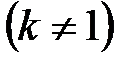 , IV
, IV 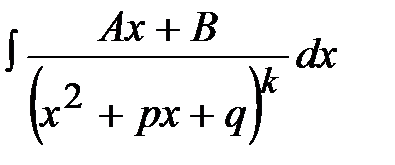 .
.
Интегралы I и II видов табличные, интегралы III вида рассмотрены в предыдущей теме, интегралы IV вида вычисляются по той же схеме, что и III вида, но в отличие от них после выделения полного квадрата возникают интегралы вида:
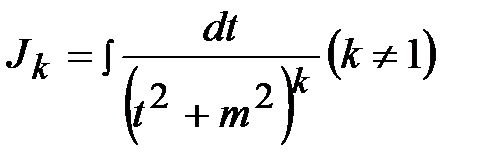 ,
,
которые находятся по рекуррентной формуле:
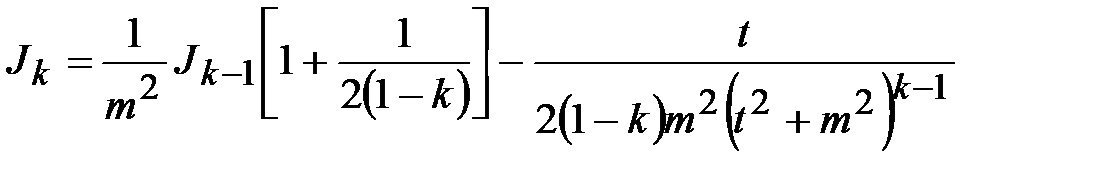 .
.
Перейдем к рассмотрению конкретных примеров вычисления интегралов от правильных рациональных дробей. Сначала рассмотрим наиболее простой случай, когда знаменатель содержит только некратные линейные множители.
Задача 15. 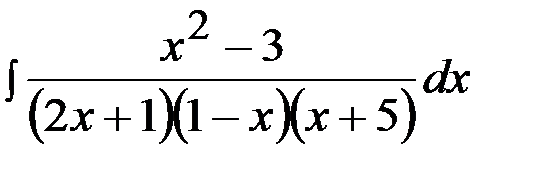 .
.
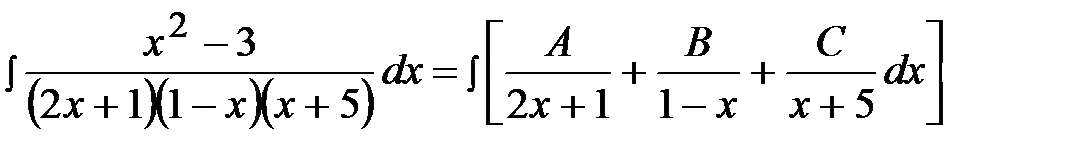 .
.
После приведения к общему знаменателю получим следующее тождество для числителей:
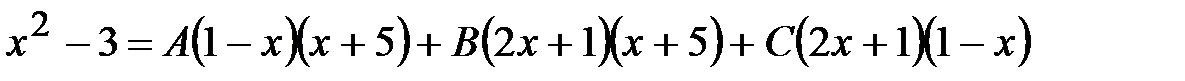 .
.
Этим тождеством мы и воспользуемся для нахождения коэффициентов А, В и С.
Если в данном тождестве в качестве 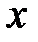 взять конкретное значение, то получим линейное уравнение относительно А, В и С. Таких уравнений нам нужно три. Полученную систему можно решить, например, методом Гаусса. Однако можно гораздо легче найти коэффициенты, если в качестве
взять конкретное значение, то получим линейное уравнение относительно А, В и С. Таких уравнений нам нужно три. Полученную систему можно решить, например, методом Гаусса. Однако можно гораздо легче найти коэффициенты, если в качестве 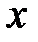 брать не произвольные числа, а корни линейных сомножителей в знаменателе. При этом в правой части тождества будет присутствовать только один из неизвестных коэффициентов.
брать не произвольные числа, а корни линейных сомножителей в знаменателе. При этом в правой части тождества будет присутствовать только один из неизвестных коэффициентов.
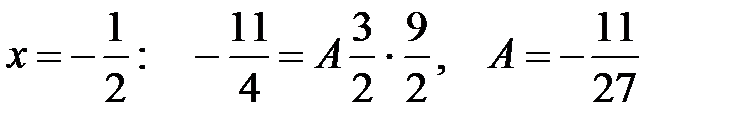
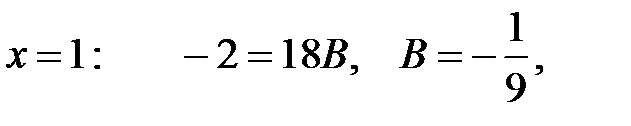
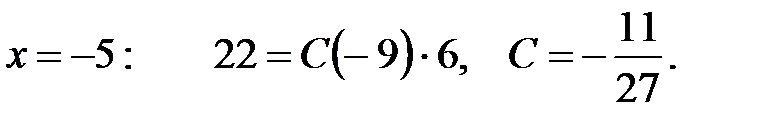
В результате получим:
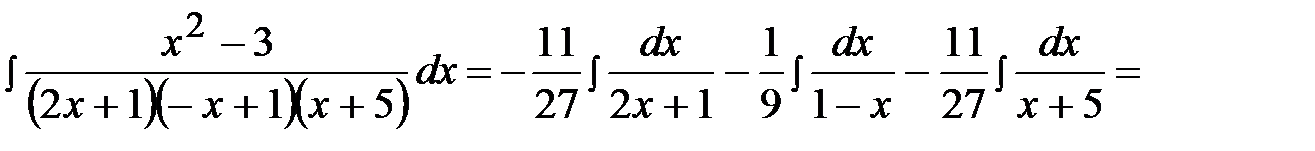
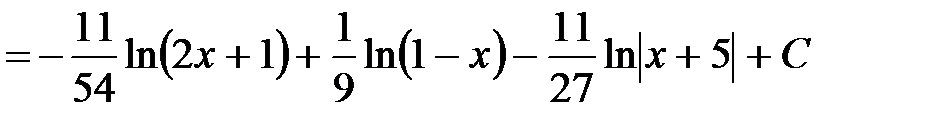 .
.
Если знаменатель содержит квадратичные сомножители, то всегда нужно проверять, не будет ли D неотрицательным. Если да, то лучше разбить его на линейные сомножители.
Задача 16. 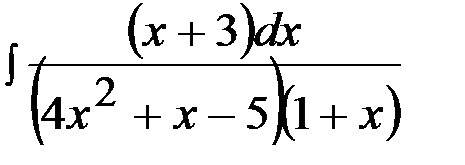 .
.
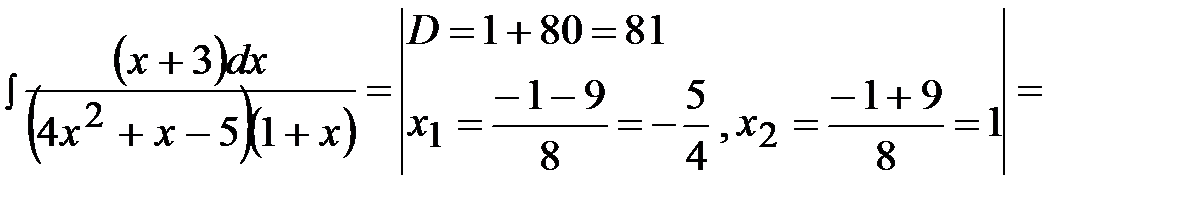
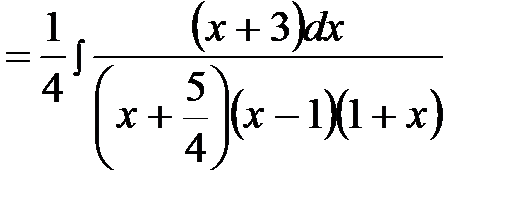 .
.
Завершите самостоятельно вычисление данного интеграла.
Перейдем к рассмотрению чуть более сложного случая, когда знаменатель содержит только линейные сомножители, причем некоторые из них кратные.
Задача 17. 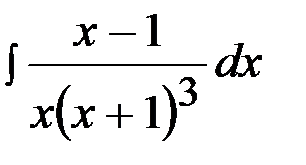 .
.
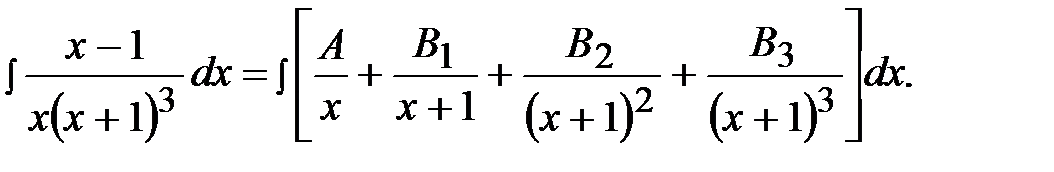
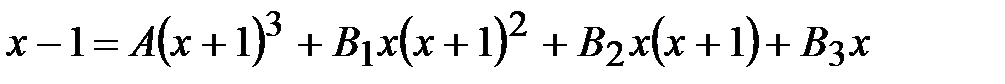 .
.
Положив последовательно 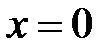 и
и 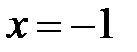 , легко найдем два неизвестных коэффициента:
, легко найдем два неизвестных коэффициента:
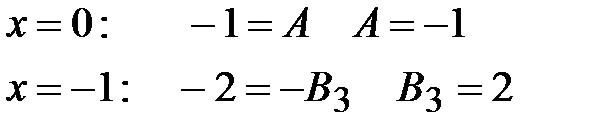
Остальные два найдем, приравняв коэффициенты при одинаковых степенях левой и правой частей тождества:
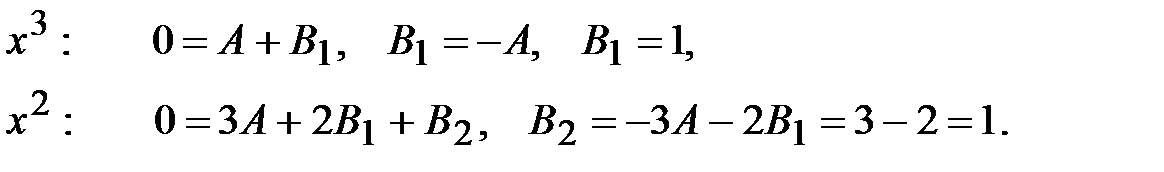
Тогда
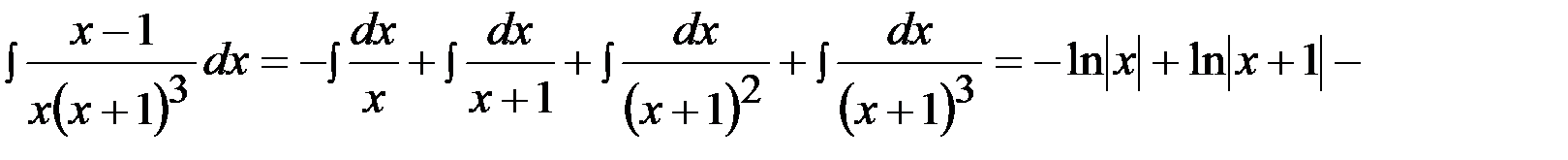
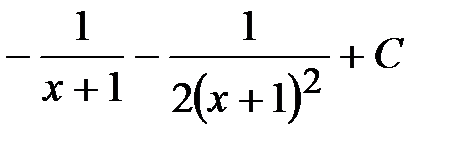 .
.
Рассмотрим теперь случай, когда знаменатель содержит некратные квадратичные сомножители с отрицательным дискриминантом.
Пример 18. 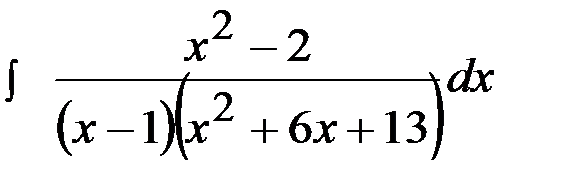 .
.
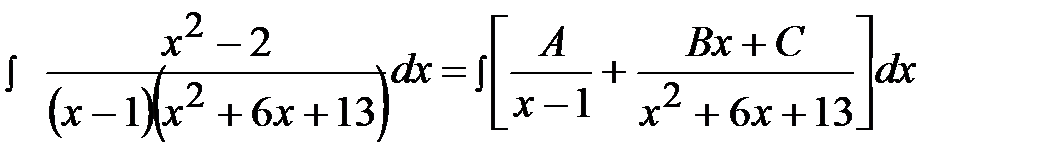 .
.
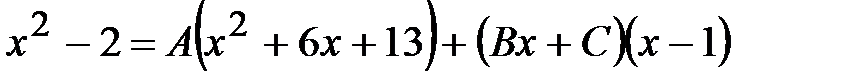 .
.
Положим 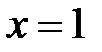 :
:
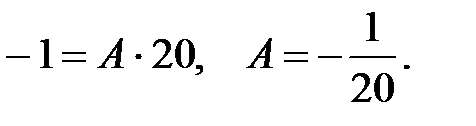
Остальные неизвестные найдем, приравнивая коэффициенты при одинаковых степенях:
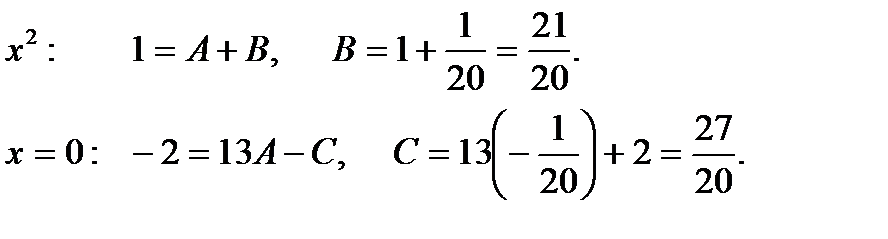
Тогда
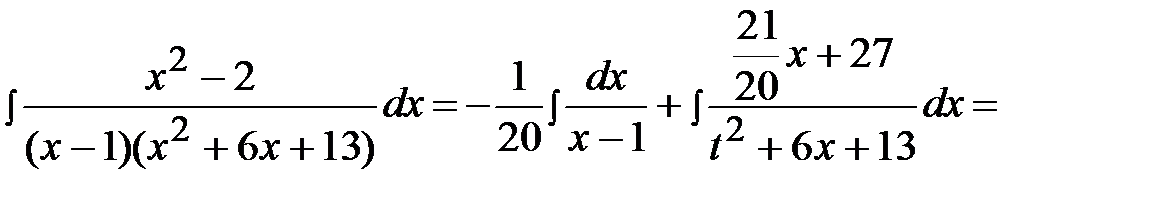
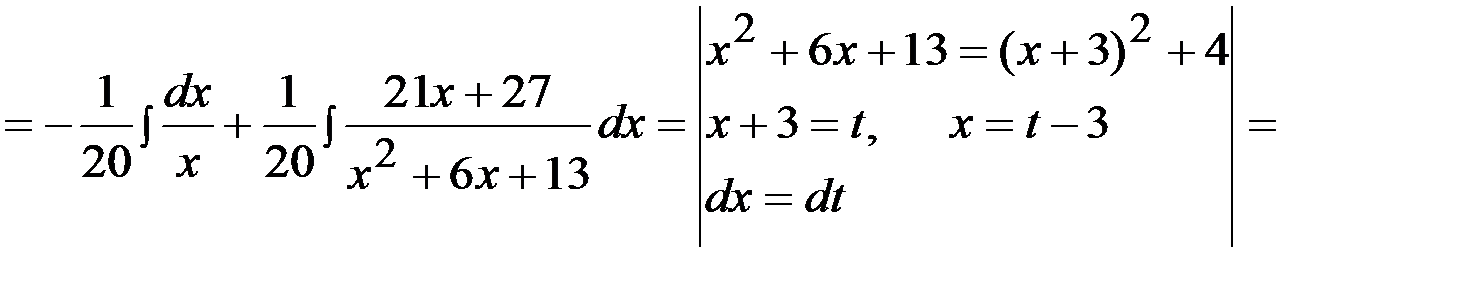
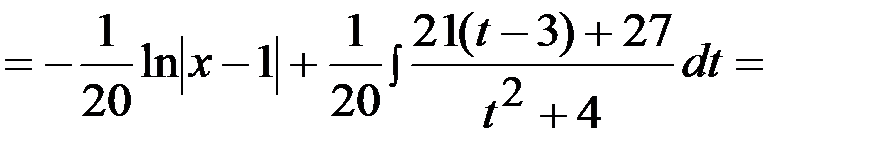
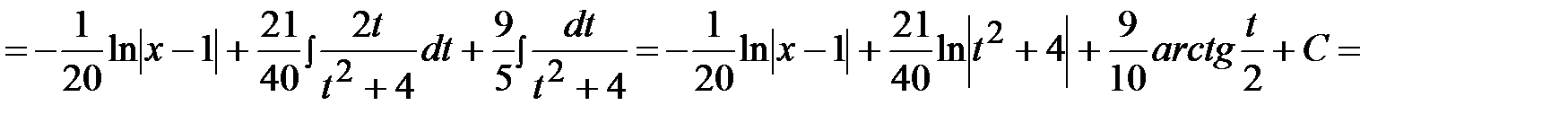
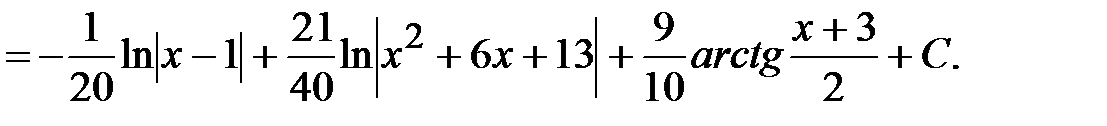
Вопросы для самопроверки
1. Сформулируйте определение первообразной функции.
2. Что называется неопределенным интегралом от данной функции?
3. Перечислите основные свойства неопределенного интеграла.
4. Напишите формулы таблицы основных интегралов.
5. В чем сущность метода интегрирования заменой переменной?
6. Напишите формулу интегрирования по частям в неопределенном интеграле. Какие функции целесообразно интегрировать по частям? Почему?
7.Как разложить рациональную дробь на простейшие?
