Статические характеристики асинхронного двигателя
Электромеханическая характеристика асинхронного двигателя определяется как зависимость 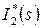 .
.
Из схемы замещения видно:
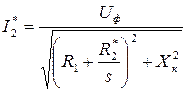 , (5.6)
, (5.6)
где 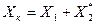 - индуктивное фазное сопротивление короткого замыкания [13; 14].
- индуктивное фазное сопротивление короткого замыкания [13; 14].
В этом случае рассматривают зависимость тока ротора не от скорости, как у ДПТ, а от скольжения S; уравнения получаются более компактные и удобные.
Если возникает необходимость перейти к традиционной электромеханической характеристике как 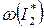 , то можно воспользоваться выражением
, то можно воспользоваться выражением 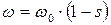 . Отметим основные точки электромеханической характеристики, изменяя
. Отметим основные точки электромеханической характеристики, изменяя 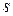 от
от 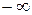 до
до 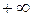 (рис. 5.3).
(рис. 5.3).
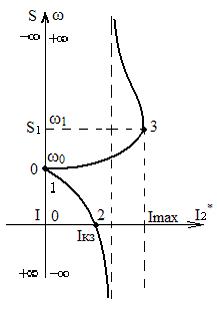
Рис. 5.3. Электромеханическая характеристика АД
1) 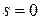 ;
; 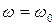 ;
; 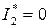 - точка идеального холостого хода;
- точка идеального холостого хода;
2) 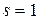 ;
; 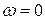 ;
; 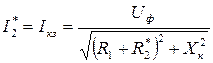 - точка короткого замыкания;
- точка короткого замыкания;
3) 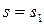
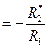 ;
; 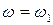 =
= 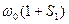 ;
; 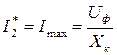 - точка максимального значения тока ротора. Она располагается в области отрицательных скольжений.
- точка максимального значения тока ротора. Она располагается в области отрицательных скольжений.
4) 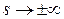 ;
; 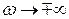 ;
; 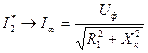 - асимптотическое значение тока ротора.
- асимптотическое значение тока ротора.
Механическую характеристику асинхронного двигателя можно определить из уравнения потерь в цепи ротора [13; 14]:
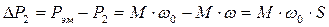 .
.
Потери в роторе часто называют потерями скольжения.
С другой стороны, пренебрегая магнитными потерями в роторе, получаем:
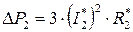 .
.
Приравнивая 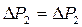 , получаем:
, получаем:
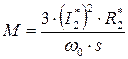 .
.
Подставив в это выражение 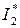 (5.6), получим уравнение механической характеристики (рис. 5.4):
(5.6), получим уравнение механической характеристики (рис. 5.4):

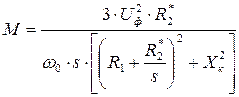 . (5.7)
. (5.7)
Если исследовать уравнение момента на экстремум 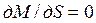 , то обнаружим наличие двух экстремальных точек. Обозначив экстремальное значение момента через
, то обнаружим наличие двух экстремальных точек. Обозначив экстремальное значение момента через 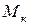 , получим:
, получим: 
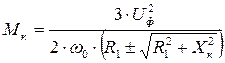 (5.8)
(5.8)
при этом соответствующее значение критического скольжения определяется как:
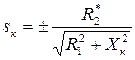 . (5.9)
. (5.9)
Знак “+” в обоих уравнениях относится к области положительных скольжений, а знак “-” к области отрицательных скольжений. Экстремальное значение момента и соответствующее ему скольжение получили название критических.
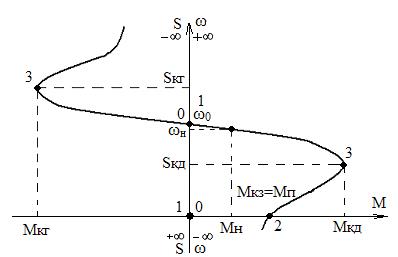
Рис. 5.4. Механическая характеристика АД
Часто уравнение момента записывают в иной форме, которая может быть получена, если разделить уравнение момента на 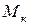 :
:
|
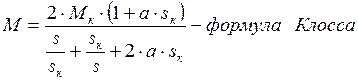 ,
, где 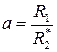 .
.
Характерные точки механической характеристики (рис. 5.4):
1) 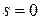 ,
, 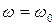 ,
, 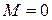 - точка идеального холостого хода;
- точка идеального холостого хода;
2) 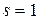 ,
, 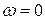 ,
, 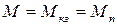 - точка короткого замыкания;
- точка короткого замыкания;
3) 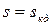 ,
, 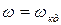 ,
, 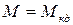 ,
, 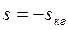 ,
, 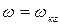 ,
, 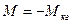 - точки максимума момента в двигательном и генераторном режимах соответственно;
- точки максимума момента в двигательном и генераторном режимах соответственно;
4) 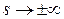 ;
; 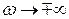 ;
; 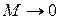 - асимптотическое значение (асимптотой является ось скорости).
- асимптотическое значение (асимптотой является ось скорости).
Приведенная механическая характеристика соответствует прямому порядку чередования фаз питающего напряжения. Если изменить порядок чередования фаз на обратный, то получим симметричную относительно начала координат характеристику. При этом двигательному режиму будет соответствовать третий квадрант.
Учитывая незначительную величину активного сопротивления статора R1, им часто пренебрегают. В этом случае а=0, а уравнение (5.10) механической характеристики выглядит так:
|
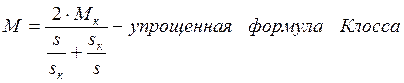 ,
, 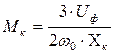 ,
, 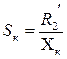 . (5.12)
. (5.12)
Если в уравнения моментов вместо текущих значений подставить номинальные, то есть 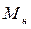 и
и 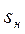 , а отношение
, а отношение 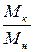 выразить через
выразить через 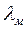 , то:
, то:
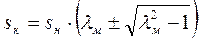 . (5.13)
. (5.13)
Используя это выражение, по каталожным данным АД можно найти 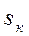 . Для АД серий 4А и АИ кратность максимального момента
. Для АД серий 4А и АИ кратность максимального момента 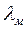 составляет примерно
составляет примерно 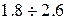 и, следовательно, критическое скольжение примерно в
и, следовательно, критическое скольжение примерно в 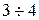 раза превышает номинальное (при знаке + в формуле (5.13)).
раза превышает номинальное (при знаке + в формуле (5.13)).
В некоторых случаях рабочий участок характеристики можно описать еще более простым выражением. Учитывая, что 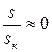 , можно записать:
, можно записать:
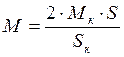 .
.
Это выражение может использоваться только на рабочем участке характеристики.
