Математическое ожидание (среднее значение)

по х:

по у:

Математическое ожидание характеризует положение случайной величины на числовой оси.

Дисперсия

по х:

по у:

Где Mx, My – математическое ожидание.

Дисперсия характеризует разброс случайных величин. В данных формулах – разброс относительно математического ожидания.

Среднее квадратическое отклонение

по х: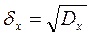

по у:

Эта величина называется также стандартным отклонением, выражается в тех же единицах, что и величины, полученные в результате эксперимента. И зачастую оказывается более удобной характеристикой, чем дисперсия. Чем слабее варьирует признак, тем меньше среднее квадратическое отклонение.

Коэффициент вариации

Коэффициент вариации необходим для сравнения изменчивости признаков, выраженных разными единицами. Дисперсия и среднее квадратическое отклонение – величины абсолютные, именованные, выражаемые в тех же единицах, что и характеризуемый ими признак.

Коэффициент вариации – относительный показатель, представляет процентное отношение среднего квадратического отклонения к математическому ожиданию

по х:

по у:

Нормированное отклонение

Нормированное отклонение – показатель, представленный отклонением той или иной величиной от математического ожидания, отнесённое к величине среднего квадратического отклонения:

по х:

по у:

Коэффициент корреляции

Коэффициент корреляции характеризует степень линейной зависимости (степень связи) между величинами х и у.

Вычисляется по формуле:

Или

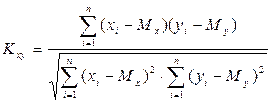
Значение К_ху изменяется в пределах от -1 до +1. Если значение К_ху > 0, то корреляция положительная (с ростом х значение у увеличивается), если К_ху < 0, то корреляция отрицательная (с ростом х значение у уменьшается).

При значении | К_ху | близком к 1 существует линейная зависимость между х и у, т.е. , знак корреляции совпадает со знаком коэффициента .

Определение значимости коэффициента корреляции

Уровень значимости коэффициента корреляции может быть определён по критерию Стьюдента:

Если , где - уровень значимости =0.95, а - число степеней свободы =n-2, то можно утверждать, что между х и у существует линейная зависимость, в противном случае – линейная зависимость отсутствует.

Значение T _табл выбирается по таблице значений критерия Стьюдента.

Отчет выполненной данной работы содержит:

1. Содержательную постановку задачи (выбор значений x и у, полученных в результате эксперимента)

2. Математическую постановку задачи (функции, по которым проводились расчеты)

3. Блок-схему алгоритма решения задач

4. Программу на алгоритмическом языке

5. Результат работы программы

6. Вывод по расчётам

7. Расчет, полученный в Excel

Содержательную постановку задачи каждый студент выполняет самостоятельно.

Пример выполнения работы

Провести расчет на Qbasic и в Excel.