Математическая постановка задачи
Лабораторный практикум
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
По курсу: «Информатика»
(раздел: «компьютерные технологии вычисления в математическом моделировании»)
Москва, 2010г.
Оглавление
Введение. 5
ЛАБОРАТОРНАЯ РАБОТА № 1 «Статистическая обработка результатов эксперимента» 5
Теоретические сведения. 6
Математическая постановка задачи. 6
Определение значимости коэффициента корреляции. 8
Пример выполнения работы.. 8
Таблица значений критерия Стьюдента. 9
БЛОК-СХЕМА.. 11
ПРОГРАММА НА ЯЗЫКЕ QBASIC.. 12
РЕЗУЛЬТАТ РАБОТЫ ПРОГРАММЫ... 14
ПРИМЕР РАБОТЫ в EXCEL.. 14
Контрольные вопросы.. 15
ЛАБОРАТОРНАЯ РАБОТА № 2 «Численное интегрирование». 15
1. Цель работы. 15
2. Основные теоретические сведения. 16
1). Метод прямоугольников. 16
2) Метод трапеций. 18
3) Метод парабол. 18
3. Порядок выполнения работы.. 19
Пример выполнения работы.. 19
БЛОК-СХЕМА.. 20
ВИД ПРОГРАММЫ НА ЯЗЫКЕ QBASIC.. 22
РЕЗУЛЬТАТЫ РАБОТЫ ПРОГРАММЫ В Qbasic. 24
Результат расчета в ППП ЭВРИКА. 25
Методические указания к выполнению лабораторной работы на ПК.. 25
Контрольные вопросы.. 26
Варианты заданий для самостоятельного решения. 26
Задание. 26
ЛАБОРАТОРНАЯ РАБОТА № 3 «Уточнение корня уравнения». 29
1. Цель работы.. 29
2. Основные теоретические положения. 29
1). Метод дихотомии. 29
2). Метод касательных. 31
3). Метод простой итерации. 31
4). Метод хорд. 33
3. Порядок выполнения работы.. 34
Пример выполнения лабораторной работы. 35
БЛОК-СХЕМА.. 36
ВИД ПРОГРАММЫ НА ЯЗЫКЕ QBASIC.. 38
РЕЗУЛЬТАТЫ РАБОТЫ В QBASIC.. 41
РЕЗУЛЬТАТЫ РАБОТЫ в Eureka. 42
Контрольные вопросы.. 42
Варианты заданий для самостоятельного решения. 43
Задание. 43
ЛАБОРАТОРНАЯ РАБОТА № 4 «Методы численного решения дифференциальных уравнений. Уравнения 1-го порядка». 48
Цель работы.. 48
Метод Эйлера. 51
Метод Эйлера - Коши. 51
Метод Руге - Кутта. 51
Правило Рунге - Ромберга. 52
Пример решения поставленной задачи. 52
БЛОК-СХЕМА АЛГОРИТМА РЕШЕНИЯ.. 53
ВИД ПРОГРАММЫ НА ЯЗЫКЕ QBASIC.. 55
Построение в Excel графика решений. 58
Контрольные вопросы.. 60
Варианты заданий к лабораторной работе. 62
ЛАБОРАТОРНАЯ РАБОТА № 5 Символьные переменные. 64
Цель работы.. 64
Инструменты обработки текстовых величин. 67
Базовые алгоритмы обработки текста. 75
Сортировка текстовых массивов. 81
Контрольные вопросы.. 93
Варианты заданий для самостоятельного решения. 94
ЛАБОРАТОРНАЯ РАБОТА № 6 Оптимизация технологического процесса. 96
Методы оптимизации функции 1-ой переменной. 96
Цель работы.. 96
Оптимизация функций одной переменной. 96
Методы оптимизации функций одной переменной. 101
Метод поразрядного приближения. 101
Метод дихотомии. 101
Метод Фибоначчи. 102
Метод золотого сечения. 103
Использование ППП Eureka и Excel при решении задач оптимизации. 104
Содержание отчета. 105
Пример выполнения лабораторной работы.. 106
БЛОК-СХЕМА.. 106
ПРОГРАММА НА АЛГОРИТМИЧЕСКОМ ЯЗЫКЕ QBASIC.. 108
РЕЗУЛЬТАТ в Qbasic. 110
Решение задачи с использованием ППП Eureka. 110
Задания. 111
Контрольные вопросы.. 112
ЛАБОРАТОРНАЯ РАБОТА № 7 Работа с файлами последовательного доступа. 112
Цель работы.. 112
Работа с файлами. 112
Требования к имени файла. 113
Расширение файла. 113
Операции над файлами. 115
Порядок выполнения работы.. 120
Содержание отчета. 121
Пример решения задачи. 121
ПРОГРАММА НА ЯЗЫКЕ QBasic. 122
РЕЗУЛЬТАТ РАБОТЫ ПРОГРАММЫ... 123
Контрольные вопросы.. 124
Варианты заданий к лабораторной работе. 124
Список литературы.. 135
Введение
Широкое внедрение математических методов в самые разнообразные сферы деятельности сегодня уже никого не удивляет. Это не только технические и экономические науки, но и развивающиеся прикладные науки управления: менеджмент, логистика, социально-экономическое прогнозирование и т.д.
Математическое моделирование становится одним из главных направлений в технике, экономике, социологии, биологии и других областях. Поэтому специалистам различных направлений необходимо владеть концепциями и методами математического моделирования, иметь представление об инструментах, применяемых в моделировании.
При изучении курса информатики, студент знакомится с основами алгоритмизации и программирования, с пакетами прикладных программ общего назначения.
Данный лабораторный практикум по курсу «Информатики» включает следующие темы:
1. статистическая обработка результатов эксперимента
2. вычисление интегралов
3. решение нелинейных уравнений
4. решение дифференциальных уравнений
5. оптимизация технологического процессов
6. работа с файлами последовательного доступа
7. символьные переменные.
ЛАБОРАТОРНАЯ РАБОТА № 1
«Статистическая обработка результатов эксперимента»
Цель работы ознакомление с основными характеристиками случайных величин.
В результате эксперимента определились такие показатели, как рост и вес человека.
| рост | х1 | х2 | х3 | ……… | ……… | ……… | ……… Хn |
| вес | Y1 | Y2 | Y3 | ……… | ……… | ……… | ……… Yn |
Обозначим хi – рост, yi – вес. Количество экспериментов- n, где n – размер выборки, i – текущий индекс.
Необходимо определить характеристики случайных величин (величин х и у).
Теоретические сведения
Дисперсия
по х:  | по у:  | Где Mx, My – математическое ожидание. |
Дисперсия характеризует разброс случайных величин. В данных формулах – разброс относительно математического ожидания.
Коэффициент вариации
Коэффициент вариации необходим для сравнения изменчивости признаков, выраженных разными единицами. Дисперсия и среднее квадратическое отклонение – величины абсолютные, именованные, выражаемые в тех же единицах, что и характеризуемый ими признак.
Коэффициент вариации – относительный показатель, представляет процентное отношение среднего квадратического отклонения к математическому ожиданию
по х:  | по у:  |
Нормированное отклонение
Нормированное отклонение – показатель, представленный отклонением той или иной величиной от математического ожидания, отнесённое к величине среднего квадратического отклонения:
по х:  | по у:  |
Коэффициент корреляции
Коэффициент корреляции характеризует степень линейной зависимости (степень связи) между величинами х и у.
Вычисляется по формуле:

Или
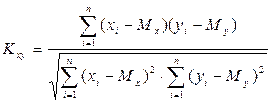
Значение Кху изменяется в пределах от -1 до +1. Если значение Кху > 0, то корреляция положительная (с ростом х значение у увеличивается), если Кху < 0, то корреляция отрицательная (с ростом х значение у уменьшается).
При значении | Кху | близком к 1 существует линейная зависимость между х и у, т.е.  , знак корреляции совпадает со знаком коэффициента
, знак корреляции совпадает со знаком коэффициента  .
.
Пример выполнения работы
Провести расчет на Qbasic и в Excel.
Таблица значений критерия Стьюдента
| f | q | |||||||
| 0.80 | 0.90 | 0.95 | 0.98 | 0.99 | 0.995 | 0.998 | 0.999 | |
| 3.0770 | 6.3130 | 12.7060 | 31.820 | 63.656 | 127.656 | 318.306 | 636.619 | |
| 1.8850 | 2.9200 | 4.3020 | 6.964 | 9.924 | 14.089 | 22.327 | 31.599 | |
| 1.6377 | 2.35340 | 3.182 | 4.540 | 5.840 | 7.458 | 10.214 | 12.924 | |
| 1.5332 | 2.13180 | 2.776 | 3.746 | 4.604 | 5.597 | 7.173 | 8.610 | |
| 1.4759 | 2.01500 | 2.570 | 3.649 | 4.0321 | 4.773 | 5.893 | 6.863 | |
| 1.4390 | 1.943 | 2.4460 | 3.1420 | 3.7070 | 4.316 | 5.2070 | 5.958 | |
| 1.4149 | 1.8946 | 2.3646 | 2.998 | 3.4995 | 4.2293 | 4.785 | 5.4079 | |
| 1.3968 | 1.8596 | 2.3060 | 2.8965 | 3.3554 | 3.832 | 4.5008 | 5.0413 | |
| 1.3830 | 1.8331 | 2.2622 | 2.8214 | 3.2498 | 3.6897 | 4.2968 | 4.780 | |
| 1.3720 | 1.8125 | 2.2281 | 2.7638 | 3.1693 | 3.5814 | 4.1437 | 4.5869 | |
| 1.363 | 1.795 | 2.201 | 2.718 | 3.105 | 3.496 | 4.024 | 4.437 | |
| 1.3562 | 1.7823 | 2.1788 | 2.6810 | 3.0845 | 3.4284 | 3.929 | 4.178 | |
| 1.3502 | 1.7709 | 2.1604 | 2.6503 | 3.1123 | 3.3725 | 3.852 | 4.220 | |
| 1.3450 | 1.7613 | 2.1448 | 2.6245 | 2.976 | 3.3257 | 3.787 | 4.140 | |
| 1.3406 | 1.7530 | 2.1314 | 2.6025 | 2.9467 | 3.2860 | 3.732 | 4.072 | |
| 1.3360 | 1.7450 | 2.1190 | 2.5830 | 2.9200 | 3.2520 | 3.6860 | 4.0150 | |
| 1.3334 | 1.7396 | 2.1098 | 2.5668 | 2.8982 | 3.2224 | 3.6458 | 3.965 | |
| 1.3304 | 1.7341 | 2.1009 | 2.5514 | 2.8784 | 3.1966 | 3.6105 | 3.9216 |
Значения критерия Стьюдента (t-критерия) для различного уровня значимости q и числа степеней свободы f (f = n-2 или n, n-число опытов).
1. Математическое ожидание: 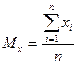 и
и 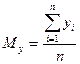
2. Дисперсия: 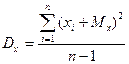 и
и 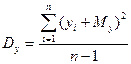
3. Среднее квадратическое отклонение: 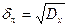 и
и 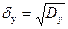
4 Коэффициент вариации: 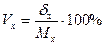 и
и 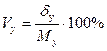
5. Нормированное отклонение: 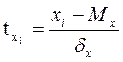 и
и 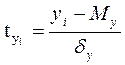
6. Коэффициент корреляции: 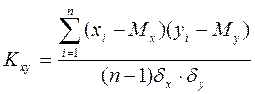
7. Критерий Стьюдента: 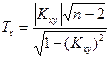
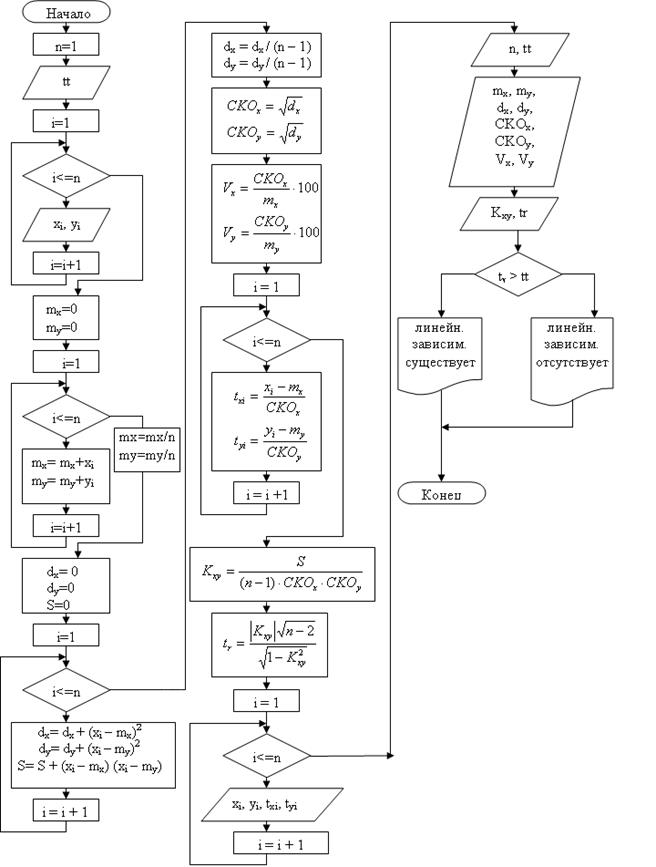
БЛОК-СХЕМА
ПРОГРАММА НА ЯЗЫКЕ QBASIC
CLS
n = 11
INPUT "Введите Коэффициент Стьюдента="; tt
DIM x(1 TO n), y(1 TO n), tx(1 TO n), ty(1 TO n)
DATA 0.001, 0.002, 0.005, 0.01, 0.04, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5
FOR i = 1 TO n
READ x(i)
NEXT i
DATA 0.98, 0.97, 0.95, 0.92, 0.9, 0.84, 0.81, 0.8, 0.8, 0.81, 0.82, 0.84
FOR i = 1 TO n
READ y(i)
NEXT i
mx = 0: my = 0
FOR i = 1 TO n
mx = mx + x(i)
my = my + y(i)
NEXT i
mx = mx / n: my = my / n
dx = 0: dy = 0: S = 0
FOR i = 1 TO n
dx = dx + (x(i) - mx) ^ 2
dy = dy + (y(i) - my) ^ 2
S = S + (x(i) - mx) * (y(i) - my)
NEXT i
dx = dx / (n - 1): dy = dy / (n - 1)
CKOx = SQR(dx): CKOy = SQR(dy)
Vx = CKOx * 100 / mx: Vy = CKOy * 100 / my
FOR i = 1 TO n
tx(i) = (x(i) - mx) / CKOx
ty(i) = (y(i) - my) / CKOy
NEXT i
Kxy = S / ((n - 1) * CKOx * CKOy)
tr = ABS(Kxy) * SQR(n - 2) / SQR(1 - Kxy ^ 2)
PRINT " N", "x", "y", "tx", "ty"
FOR i = 1 TO n
PRINT i, x(i), y(i), tx(i), ty(i)
NEXT i
PRINT "число ответов ="; n
PRINT "табличное значение критерия Стьюдента ="; tt
PRINT "математическое ожидание :"; "по x="; mx, "по y="; my
PRINT "дисперсия :"; "по x="; dx, "по y="; dy
PRINT "среднеквадратическое отклонение :"; "по x="; CKOx, "по y="; CKOy
PRINT "коэффициент вариации :"; "по x="; Vx, "по y="; Vy
PRINT "коэффициент корреляции ="; Kxy
PRINT "рассчитанное значение критерия Стьюдента ="; tr
IF tr >= tt THEN
PRINT "линейная зависимость между x и y Cуществует"
ELSE
PRINT "линейная зависимость между x и y Отсутствует"
END IF
END
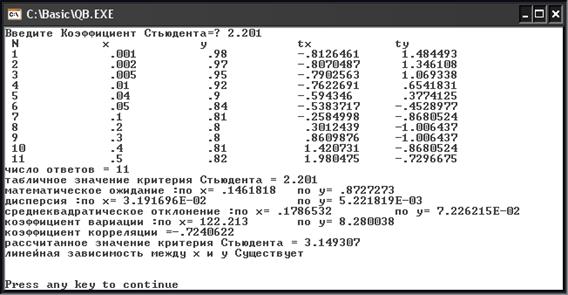
РЕЗУЛЬТАТ РАБОТЫ ПРОГРАММЫ
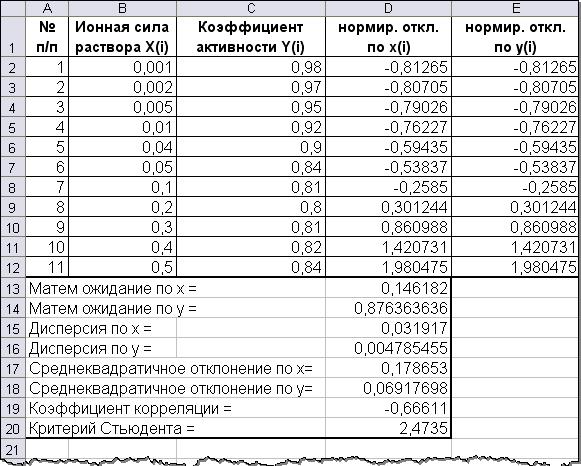
ПРИМЕР РАБОТЫ в EXCEL
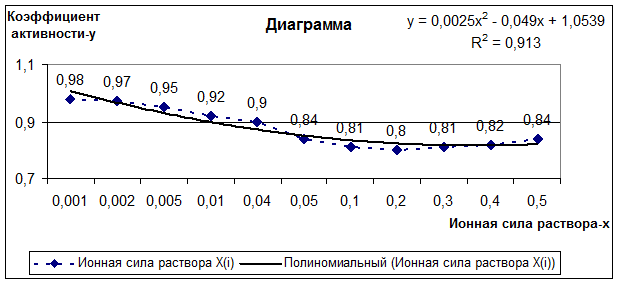
 Результаты эксперимента
Результаты эксперимента
Контрольные вопросы
«Статистическая обработка результатов эксперимента»
1. Что характеризует математическое ожидание?
2. Какие характеристики оценивают разброс случайных величин?
3. Как определяется дисперсия?
4. Для чего необходим коэффициент вариации?
5. Как определить нормированное отклонение?
6. Что характеризует коэффициент корреляции?
7. В каких пределах измеряется коэффициент корреляции?
8. Как определить уровень значимости коэффициента корреляции?
9. Как выбирается Ттабл?
10. Какое соотношение должно быть между Трасч и Ттабл, для утверждения, что линейная зависимость существует?
ЛАБОРАТОРНАЯ РАБОТА № 2
«Численное интегрирование»
Цель работы.
Ознакомится с принципом модульного программирования на примере задачи численного интегрирования. Использование оболочки QBASIC для построения процедур программ.
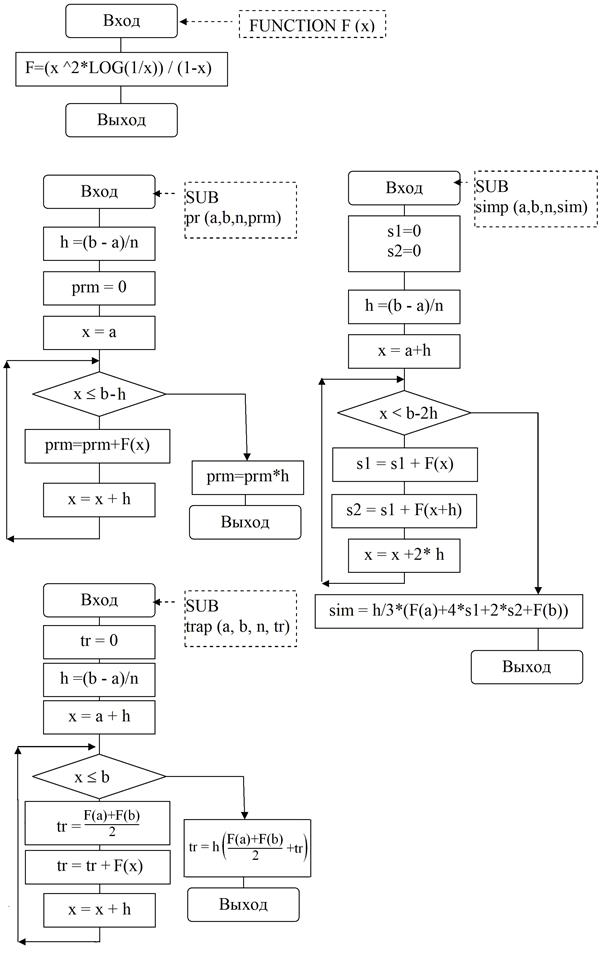
Метод прямоугольников
В Методе прямоугольников непосредственно используется замена определенного интеграла интегральной суммой. В качестве точек xi; могут выбираться левые (xi-1) или правые (xi) границы элементарных отрезков. Расчетные формулы можно записать так:
При выборе левых границ (см. рис.1)
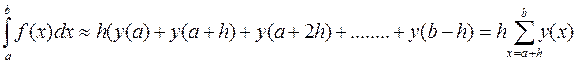
 |
При выборе правых границ (см. рис.2)
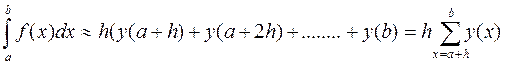
 |
При выборе границ от a+ h/2 до b-h/2
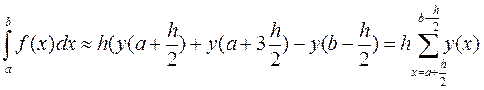
 |
Рис.4
Метод трапеций
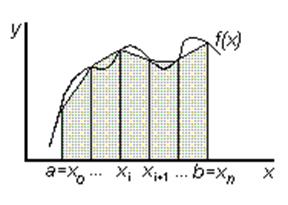 |
В методе трапеций график функции f(х)аппроксимируется ломаной, соединяющей точки с координатами
(xi, у)
Рис.5
Искомое значение определенного интеграла представляется в виде суммы площадей трапеций, построенных на каждом из элементарных отрезков:
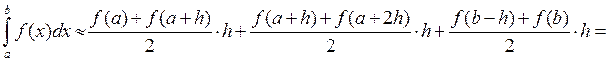
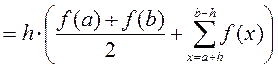
Метод парабол
В методе парабол (формула Симпсона) на каждом из элементарных отрезков по трем известным значениям функции f(Xj) строится парабола, заданная уравнением aх2+bх+с.
Формула для нахождения определенного интеграла может быть выведена из условия равенства значений: уi = aхi2+ bxi +с:
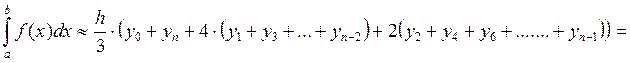
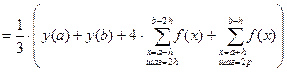
3. Порядок выполнения работы
| |
3.1. Получить у преподавателя вариант задания, включающий в себя подынтегральную функцию (F(Х)), отрезок интегрирования (a,b), точность вычисления значения интеграла (eps).
3.2. Исследовать подынтегральную функцию на непрерывность и существование на заданном отрезке.
3.3. Составить блок-схему для каждого метода и блок-схему головного модуля.
3.4. Написать подпрограмму для каждого метода (прямоугольников, трапеции, парабол).
3.5. Написать головной модуль.
3.6. Отладить программу и получить результаты .
3.7. Проанализировать полученные результаты и сделать выводы.
4. Содержание отчета.
4.1. Математическая постановка задачи.
4.2. Исходные данные.
4.3. Краткое описание методов. Блок-схема для каждого метода. Листинг подпрограмм.
4.4. Блок-схема головного (или управляющего) модуля. Листинг.
4.5. Распечатка полученных результатов.
4.6. Сравнительный анализ полученных результатов разными методами.
Пример выполнения работы
Вычислить интеграл 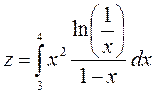
БЛОК-СХЕМА
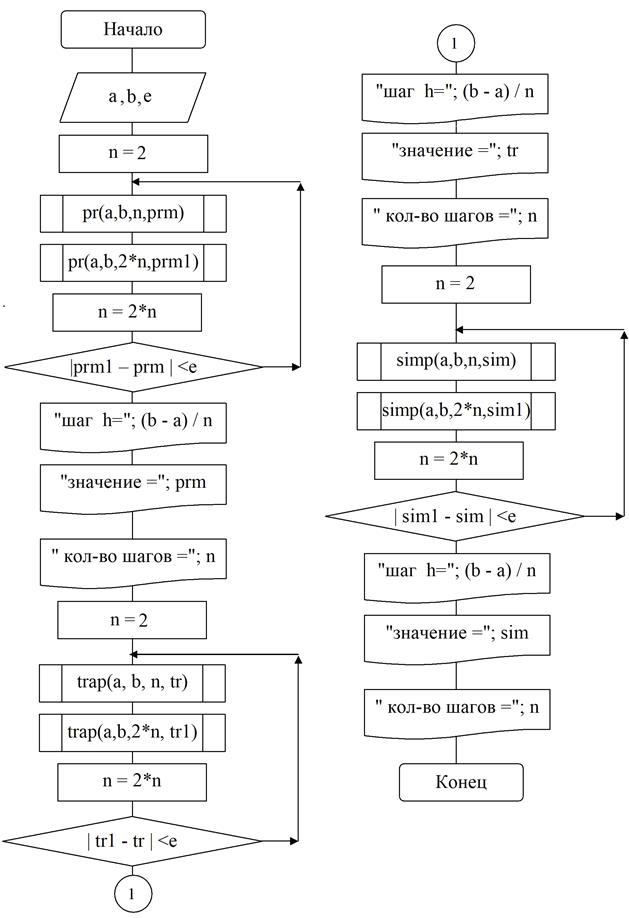
Задание
Вычислить интеграл тремя методами: прямоугольников, трапеций и методом парабол (Симпсона), используя автоматический выбор шага интегрирования.
Точность вычислений ε =10-4.
Таблица заданий № 1.
| № п/п | Уравнение | № п/п | Уравнение | № п/п | Уравнение |
 |  |  | |||
 | 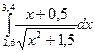 | 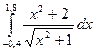 | |||
 |  |  | |||
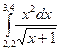 |  |  | |||
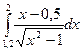 |  | 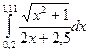 | |||
 | 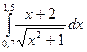 |  | |||
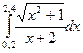 |  | 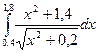 | |||
 | 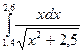 |  | |||
 | 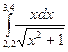 | 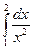 | |||
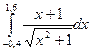 |  |  |
Таблица заданий № 2.
| № п/п | Уравнение | № п/п | Уравнение | № п/п | Уравнение |
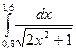 |  |  | |||
 |  | 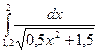 | |||
 | 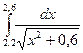 | 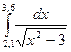 | |||
 | 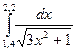 |  | |||
 |  | 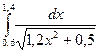 | |||
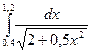 |  | 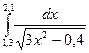 | |||
 |  | 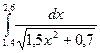 | |||
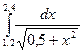 |  |  | |||
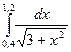 | 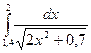 |  | |||
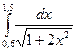 | 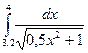 | 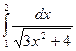 |
ЛАБОРАТОРНАЯ РАБОТА № 3
«Уточнение корня уравнения»
Цель работы
Получить навыки модульного программирования на примере задачи численного решения нелинейных уравнений. Использование оболочки QBasic для построения программ и головного модуля.
Метод дихотомии
Пусть функция f (x) отрицательна в точке a (f (a) < 0), положительна в точке b (f (b) > 0), и непрерывна на отрезке [a, b] график функции пересекает ось Х, т. е. на этом отрезке имеется корень уравнения – точка, в которой
f(х)= 0.
Тот же вывод следует, если f(а) > 0, f(b) < 0. В общем виде это формулируется так: в точках а и b функция f(х) принимает значения разных знаков. Если нам известен хотя бы один такой отрезок, пусть и большой длины, мы можем построить процедуру быстрого и сколь угодно точного поиска корня уравнения. Найдем значение функции в точке с, находящейся в середине отрезка: с =(a + b)/2. Знак f(с) совпадает со знаком функции на одном из концов отрезка и противоположен знаку функции на другом конце.
Пусть разные знаки f(х) в точках а и с. Значит на [а, с] наверняка есть искомый корень уравнения.
Таким образом, мы получили задачу, эквивалентную исходной, но теперь длина отрезка, на котором, как нам известно, находится корень, в два раза короче. Отрезок [а, с] опять можно разделить пополам и оставить в рассмотрении только один из двух получившихся (учитывая знаки значений f(х) на концах этих отрезков). Выбранный отрезок вновь разделить, и продолжать так до тех пор, пока отрезок, на котором находится корень, не станет достаточно мал.
Метод касательных
Метод Ньютона, или метод касательных основан на вычислении не только значений функции, но и значений ее производной. Разложим f(х) в ряд Тейлора и отбросим члены ряда выше второго порядка:
f (х) = f (х0) + f’ (х0)(х – x0)
В этом приближении корень функции легко найти по формуле:
f (x) = 0, при xi = xi+1 – f (x0)/f ' (x0)
Для нелинейных функций это, конечно, не точное равенство, но способ получить значение, более близкое к корню. Таким образом, метод Ньютона состоит в построении последовательности итераций:
x1 = x0 – f (x0)/ f ' (x0)
x2 = x1 – f (x1)/ f ' (x1)
xi+1 = xi – f (xi)/ f ' (xi)
На какой итерации завершать процесс нахождения корня? Возможно два варианта: либо когда значение функции станет достаточно маленьким по абсолютной величине:
| f (x)| < eps, либо когда практически перестанет меняться значение х:
| f (x)/ f '(x)| < eps
| Xi+1 – Xi| <= eps
Метод простой итерации
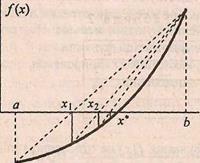
Рассматриваемый метод реализует третий подход к решению задачи. Предварительно исходное уравнение f(х) = 0 преобразуют к виду φ(х)=х, что является частным случаем более общей структуры g(х)=f(x).Затем выбирают начальное значение х0 и подставляют его в левую часть уравнения, но φ(x)≠х0, поскольку x0 взято произвольно и не является корнем уравнения.
Полученное φ(x)=x1 рассматривают как очередное приближение к корню. Его снова подставляют в правую часть уравнения φ(х1) и получают следующее значение х2 (х2 = φ(x1) и т.д., в общем случае хi+1 =φ(хi). Получающаяся таким образом последовательность х0, x1, х2, х3, х4,… при определенных условиях может сходиться к корню х* (рис. 1.a).
Условие сходимости |φ’(x)| <= 1 на [а,b], причем, чем ближе модуль к нулю, тем выше окажется скорость сходимости к решению. В противном случае последовательность расходится от искомого решения (“метод не сходится”).
На рисунке 2 приведён один из возможных случаев, когда итерационный
процесс не сходится. Видно, что последовательность х0, x1, х2,… удаляется от
корня х*. Это всегда будет иметь место в том случае, если тангенс угла наклона φ(x) в окрестности корня по модулю больше единицы.
Существуют различные способы преобразования уравнения f(x) = 0 к виду φ(x) = x; одни могут привести к выполнению условия сходимости всегда, другие – в отдельных случаях.
Самый простой способ следующий:
f(x) + x = 0 + x, f(x) + x = φ(x)
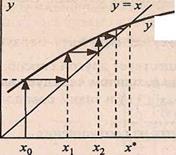 |  |  |
| (а) | (б) | (в) |
| а) 0 < φ’(х) < 1; | б) – 1 < φ’(х) < 0 | |
| Pис.6 |
но он не всегда приводит к успеху. Существует другой способ, в соответствии с которым φ(х)=х-f(х)/к, причем k следует выбирать так, чтобы
|k| >Q/2, где Q=mах |f'(х)| и знак к совпадал бы со знаком f'(х) на [а, b].
Погрешность решения можно оценить из соотношения
|x* - xi| <= (q/(1 – q))*|X(i) – X(i+1)|, где q = max φ(х), на отрезке [a,b].
Вследствие этого для окончания вычислений в методе итераций применят соотношение (q/(q – 1))*|X(i) – X(i + 1)|<= ε, где ε — заданная погрешность решения.
Часто используют упрощенное условие окончания поиска
|X(i) – X(i + 1)|<=ε не вычисляя максимальное значение производной, но в этом случае погрешность решения может не соответствовать заданной (т.е. быть больше или меньше).
4). Метод хорд
В этом методе нелинейная функция f(х) на отделенном интервале [а, b]
заменяется линейной, в качестве которой берется хорда — прямая,
стягивающая концы нелинейной функции. Эта хорда определяется как прямая, проходящая через точки с координатами (а, f(a)) и (b,f(b)). Имея уравнение хорды у = сх + d, можно легко найти точку ее пересечения с горизонтальной осью, подставив в уравнение у = 0 и найдя из него х. Естественно, в полученной таким путем точке x1 не будет решения, ее принимают за новую границу
отрезка, где содержится корень. Через эту точку с координатами (x1, f(x1)) и соответствующую границу предыдущего интервала опять проводят хорду, находят х2 и т.д. несколько раз, получая последовательностьх3 , х4 ,х5,..., сходящуюся к корню.
Метод хорд применим только для монотонных функций.
Алгоритм метода зависит от свойств функции f(х). Если f(b)*f ”(b) > 0, то строящаяся на каждом этапе хорда имеет правый фиксированный ("закрепленный") конец, и алгоритм выглядит следующим образом:
xi+1=xi-(f(xi)/(f(b)-f(xi)))*(b-xi);
при этом последовательность х1 ,х2,,…будет приближаться к корню слева.
Если f(а)f"(а) > 0, то строящаяся на каждом этапе хорда имеет левый фиксированный ("закрепленный") конец, и алгоритм выглядит следующим образом: xi+1 = a +( f(a) / (f(a) – f(xi)))*(xi – a);
 |
| Рис.7 |
при этом последовательность х1 ,х2,… будет приближаться к корню справа.
На рисунке 7 приведен один из вариантов применения метода хорд. В рассматриваемом случае "закрепленным" является правый конец. Приведено пять шагов (пять хорд), при этом к решению приближаемся слева.
Теоретически доказано, что если первые производные на концах интервала при монотонной и выпуклой функции f(х) не различаются более чем в 2 раза, то справедливо соотношение |х* - хi| < |хi – хi-1| и условием прекращения пополнения последовательности может быть |хi+1 - хi| <= ε, а в качестве корня принято xi+1 (можно также окончить процесс и при достижении f(хi) <= δ, о чем указывалось в концепции методов). На практике указанные условия можно применять и без предварительной проверки производных, отклонение погрешности результата при пологих функциях не будет существенным.
Порядок выполнения работы
1. Получить у преподавателя вариант задания, включающий в себя трансцендентное или алгебраическое уравнение ( F(x) = 0), отрезок для поиска решения ( a, b), точность вычисления значения корня (eps) и задание, каким из методов (все методы) решить задачу.
2. Исследовать существование корня на заданном отрезке, требования к функции: разные знаки на концах отрезка, непрерывность).
3. Выяснить, с какой стороны отрезка строить приближение к решению уравнения: если знак второй производной совпадает со знаком функции
(f(х)- f"(х) > 0), то приближение строим елевой стороны отрезка, в противном случае - с левой стороны.
4. Написать подпрограмму для вычисления функции F(х).
5. Написать подпрограмму, например для первого метода дихотомии.
6. Написать подпрограмму, например, для второго метода касательных или простой итерации.
7. Найти первую производную функции F(x) и оформить её вычисление процедурой функции (для метода касательных).
8. Найти приведённую функцию и оформить её вычисление процедурой функции.
9. Написать головной модуль.
10. Отладить программу и получить результат.
Пример выполнения лабораторной работы.
| Уравнение | Отрезок | Точность |
| y = x - 2 + SIN(1 / x) | (1.2; 2) | 10ˉ³ |
Решить уравнение методом дихотомии, простой итерации, методом касательных.
a=1.2
b=2
F(x) = x - 2 + SIN(1 / x) - исходная функция
G (x) = 2 - SIN(1 / x) - приведенная функция
F1 (x) = 1+cos(1/x) 1-ая ПРОИЗВОДНАЯ ОТ F
F2 (x) = -sin(1/x) 2-ая ПРОИЗВОДНАЯ ОТ F
G1(x)=-cos(x) 1-ая ПРОИЗВОДНАЯ ОТ G
e = 0.001
БЛОК-СХЕМА



РЕЗУЛЬТАТЫ РАБОТЫ В QBASIC

РЕЗУЛЬТАТЫ РАБОТЫ в Eureka.
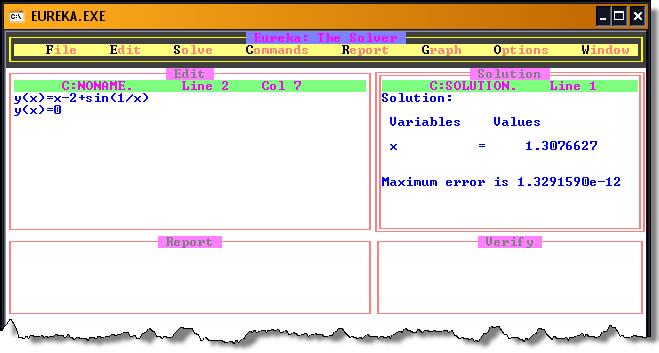
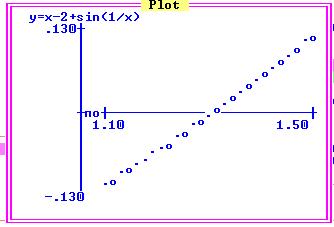
Рекомендации по решению задачи:
1. Решить задачу, используя ППП Eureka.
2. Исходя из полученного решения, выбрать границы существования корня.
3. Составить блок – схему решения и программу на QBasic.
Контрольные вопросы
1. В чем заключается геометрический смысл метода половинного деления?
2. Какой оператор цикла используется в процедуре дихотомии?
3. Какими свойствами должна обладать функция F(x), чтобы методом половинного деления можно было гарантировать решение уравнения F(x)?
4. Что необходимо для нахождения хотя ы одного действительного корня уравнения F(x) методом половинного деления?
5. Какие процедуры функции используются в программе?
6. Какой функцией заменяется левая часть уравнения F(x)=0 в методе итерации?
7. Что называется сходимостью метода итерации?
8. Каково условие сходимости метода итерации и как это условие проверяется в программе?
9. В чем заключается геометрическая интерпретация метода Ньютона?
10. Исходя из чего выбирается в методе Ньютона первое приближение Х0
11. для чего в программе предусмотрена процедура-функции для второй производной от исходной функции?
Варианты заданий для самостоятельного решения
Задание.
1. Уточнить корень уравнения, используя следующие методы:
- метод половинного деления;
- метод простой итерации;
- метод касательных (Ньютона).
2. Для вариантов заданий, представленных в таблице 4, выбрать точность вычисления.
3. Для вариантов заданий, представленных в таблице 6, вычислить корень с заданной точностью.
4. Для вариантов заданий, представленных в таблице 7,8,9, установить границы существования корня, точность вычисления, установить границы существования корня.
Таблица заданий № 4.
| П\П | Вид уравнения | Начальное приближение корня |
| 1. | x – sin 2x – 1 = 0 | |
| 2. | 2x ^ 3 + 4x – 1 = 0 | 0.1 |
| 3. | x ^ 3 + 12x – 2 = 0 | 0.95 |
| 4. | 5 – x – 8lnx = 8 | 4.32 |
| 5. | x ^ 3 + x = 1000 | 9.42 |
| 6. | x – sin x = 0.25 | 1.17 |
| 7. | x ^ 3 – 6x ^ 2 + 20 = 0 | 2.25 |
| 8. | 5x ^ 3 + 10x ^ 2 + 5x – 1 = 0 | 0.6 |
| 9. | 3sin 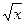 +0.34x-3.8 =0 +0.34x-3.8 =0 | |
| 10. | x – 3 + sin (3.6x) = 0 | |
| 11. | arcos(x)-  = 0 = 0 | |
| 12. | √1- 0.4x ^ 2 – arcsin x = 0 | |
| 13. | x – 2 + sin x = 0 | 1.2 |
| 14. | 1 – x + sin x – ln (1 + x) = 0 | |
| 15. | x ^ 2 – ln (1 + x) – 3 = 0 | |
| 16. | x ^ 3 + x ^ 2 – 3 = 0 | 0.6 |
| 17. | x ^ 3 – x – 0.2 = 0 | 0.9 |
| 18. | 5x ^ 3 – x – 1 = 0 | 0.6 |
| 19. | x ^ 3 – 2x – 5 = 0 | 1.9 |
| 20. | x ^ 3 + x = 1000 | 9.1 |
| 21. | x ^ 4 + 2x ^ 3 – x – 1 = 0 | |
| 22. | x ^ 3 – x – 2 = 0 | 0.9 |
| 23. | x – sin x/2 – 1 = 0 | |
| 24. | 2 ^ 3 + 4x – 1 = 0 | 0.1 |
| 25. | x ^ 3 + 12x – 2 = 0 | 0.95 |
Таблица заданий № 5
| П\П | Вид уравнения | Отрезок |
| 1. | 0.25x ^ 3 + x – 1 .2502 = 0 | 0, 2 |
| 2. | 0.1x ^ 2 – xlnx = 0 | 1, 2 |
| 3. | 3x – 4lnx – 5 = 0 | 2, 4 |
| 4. | e ^ x – e ^ -x – 2 = 0 | 0, 1 |
| 5. | e ^ x + lnx – 10x = 0 | 3, 4 |
| 6. | 3x – 14 + e ^ x – e ^ -x = 0 | 1, 3 |
| 7. | 3ln ^ 2x + 6lnx– 5 = 0 | 1, 3 |
| 8. | 2xsinx – cosx = 0 | 0.4, 1 |
| 9. | xtgx – 1\3 = 0 | 0.2, 1 |
| 10. | √ 1 – x - cos√ 1 – x = 0 | 0, 1 |
Таблица заданий № 6
| № вар. | Уравнение | Интервал | Точность |
| 1. | x – 1\ (2 + sin2x) = 0 | [0; 1] | 10 ־³ |
| 2. | arcsin(x\3) - √ 1 – (x\3) ^ 2 = 0 | [ 1,5; 3] | 10 ־³ |
| 3. | x - √ 9 –x+ x ^ 2 = 0 | [2; 3] | 10 ־³ |
| 4. | √1 – x ^ 2 - arcsin x = 0 | [0; 1] | 10 ־³ |
| 5. | tgx – (1/3)(tgx)^3 + (1/5)(tg x) ^ 5 – 1/3 = 0 | [0; 0,8] | 10 ־³ |
| 6. | e ^ x – e (- x) – 2 = 0 | [0; 1] | 10 ־³ |
| 7. | cosx – e(-(x ^ 2) / 2) + x – 1 = 0 | [0; 2] | 10 ־³ |
| 8. | sin(x ^ 2) + cos( x ^ 2) – 10x = 0 | [0; 1] | 10 ־³ |
| 9. | 3sin√x + 0,35x – 3,8 = 0 | [2; 3] | 10 ־³ |
| 10. | √1 – 0,4 (x ^ 2) – arcsinx = 0 | [0; 1] | 10 ־³ |
| 11. | 1/4(x ^ 3) + x – 1,25 = 0 | [0; 1] | 10 -5 |
| 12. | x – sin(x + 2) = 0 | [0; 1] | 10 -5 |
| 13. | √1 – x - cos√1 – x = 0 | [0; 1] | 10 ־³ |
| 14. | 0,1(x ^ 2) – x lnx = 0 | [1; 2] | 10 ־³ |
| 15. | 3x – 4 lnx – 5 = 0 | [1;4] | 10 ־³ |
| 16. | e ^ x + lnx – 10 x = 0 | [1; 4] | 10 ־³ |
| 17. | x tgx – 1/3 = 0 | [0; 1] | 10 ־³ |
