Критерии подобия и критериальные уравнения
После приведения уравнения Навье-Стокса к следующему виду они стали содержать следующие типы переменных: 1) безразмерные независимые переменные 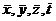 ; 2) безразмерные зависимые переменные
; 2) безразмерные зависимые переменные  ; 3) безразмерные критерии – комплексы, состоящие из величин заданных по условиям однозначности
; 3) безразмерные критерии – комплексы, состоящие из величин заданных по условиям однозначности  .
.
После приведения к безразмерному уравнению изменился характер уравнений. Уравнения приобрели обобщенный вид, т.к. одно и то же значение любого критерия может быть получено путем бесконечного варьирования входящих величин.
Критерии подобия могут быть двух видов: 1) состоящие из разноименных параметров; 2) имеющие периодический вид, т.к. представляют собой отношение одноименных параметров.
Относительные переменные также могут быть двух видов:
1) отношение переменной к одноименной величине, заданной по условию однозначности:

2) если по условию однозначности нельзя задать одноименную величину, то строится комплекс приводящий величину к безразмерному виду – число подобия: 
В числа подобия входят определяемая величина. Критерий подобия состоит из заранее известных величин, заданных по условиям однозначности..
1) Критерий Рейнольдса  - определяет соотношение сил инерции и вязкости в однородном потоке. Это важнейший гидродинамический критерий для вынужденного движения.
- определяет соотношение сил инерции и вязкости в однородном потоке. Это важнейший гидродинамический критерий для вынужденного движения.
2) Критерий гидродинамической гомохронности 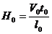 - определяет соотношение между периодом темпа внешних воздействий на поток и периодом перестройки скоростного поля.
- определяет соотношение между периодом темпа внешних воздействий на поток и периодом перестройки скоростного поля.
3) Критерий Фруда  - определяет соотношение между силами инерции и тяжести в потоке. Используется только в задачах, в которых гравитационные эффекты имеют важное значение.
- определяет соотношение между силами инерции и тяжести в потоке. Используется только в задачах, в которых гравитационные эффекты имеют важное значение.
4) Число Эйлера  - определяет соотношение сил давления и сил инерции; определяемая величина; т.к. часто давление в потоке неизвестно, то больший интерес представляет определение перепада давления на рассматриваемом участке
- определяет соотношение сил давления и сил инерции; определяемая величина; т.к. часто давление в потоке неизвестно, то больший интерес представляет определение перепада давления на рассматриваемом участке 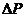 .
.
53. Условия подобия физических процессов:
1. Подобные процессы должны быть качественно одинаковыми, т.е. они должны иметь одинаковую физическую природу и описываться одинаковыми по форме записи дифференциальными уравнениями.
2. Условия однозначности подобных процессов должны быть одинаковыми во всем, кроме числовых значений размерных постоянных, содержащихся в этих условиях.
3. Одноименные определяющие безразмерные переменные подобных процессов должны иметь одинаковое числовое значение.
По первому условию (Подобные процессы должны быть качественно одинаковыми, т.е. они должны иметь одинаковую физическую природу и описываться одинаковыми по форме записи дифференциальными уравнениями):
При рассмотрении свободного движения в большом объеме можно пренебречь градиентом давления в жидкости. Исключение градиента давления из уравнения движения приводит к иной записи уравнения, меняется класс рассматриваемого явления.
Таким образом, отдельные разновидности процессов конвективного теплообмена могут описываться различными дифференциальными уравнениями (хотя они были частными случаями более общих уравнений), и в этом случае они будут принадлежать к различным классам явлений.
По второму условию (Условия однозначности подобных процессов должны быть одинаковыми во всем, кроме числовых значений размерных постоянных, содержащихся в этих условиях):
По третьему условию (одноименные определяющие безразмерные переменные подобных процессов должны иметь одинаковое числовое значение.
