Внутренняя энергия как характеристическая функция

Энтальпия как характеристическая функция

Энтальпия является характеристической функцией, когда в качестве переменных используют Р и S.

В этом уравнении энтальпия является такой функцией: H=H(p,S)

Эти производные определили в явном и простейшем виде термодинамические свойства системы и, следовательно, энтальпия в зависимости от переменных S и Р является характеристической функцией.

Энтальпия как характеристическая функция также малоудобна для расчетов, так как в качестве одного из параметров в функцию входит энтропия, которую нельзя замерить и трудно поддержать ее постоянной величиной.

Свободная энергия как характеристическая функция.

свободная энергия,F= F (T,v).

К основным свойствам характеристических функций относятся следующие.

1. Термодинамические потенциалы отличаются от других функций тем, что имеют более простую структуру и определенное физическое значение.

2. Параметры состояния системы равны частным производным от термодинамического потенциала, взятым по тем же параметрам.

3. В результате дифференцирования термодинамического потенциала получается полный дифференциал данной функции.

4. Используя характеристические функции, записанные в дифференциальном виде, можно получить любые термодинамические параметры системы.

5. Термодинамический потенциал всей системы складывается из значений потенциала ее частей, т. е. обладает свойством аддитивности.

6. Характеристические функции устанавливают зависимость между различными термодинамическими свойствами вещества. Так, например, первые производные от потенциала характеризуют термические свойства (т. е. величины, измеряемые непосредственно приборами – объем, температура, давление), а вторые производные соответствуют калорическим свойствам системы (это величины, выраженные в единицах теплоты – теплоемкость, энтропия, энтальпия, внутренняя энергия).

7. Частные производные характеристических функций позволяютсоставлять уравнения теплоемкостей C_v и C_p, уравнения состояния и другие термодинамические зависимости.

8. Функция является характеристической только при определенных параметрах. При выборе других переменных она утрачиваетсвои свойства, потому что в этом случае частные производные не выражают термодинамические свойства системы.

Изобарно-изотермный потенциал как характеристическая функция.

27. Связь между 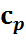и 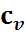для реального газа

Уравнение Ван-дер-Ваальса

Как отмечалось ранее, при низких температурах и высоких давлениях уравнение Менделеева – Клапейрона для одного моля вещества дает существенные отклонения от значений, измеряемых на опыте.

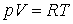
Были сделаны многочисленные попытки найти уравнение состояния для реального вещества, которое могло бы охватить, если не все состояния вещества, то хотя бы газообразное и жидкое. Из множества предложенных уравнений наибольшей известностью пользуется уравнение Ван-дер-Ваальса:

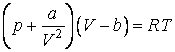
записанное для одного моля вещества. Для молей это уравнение имеет вид:

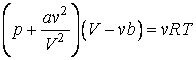
Постоянные a и b определяются экспериментально и имеют различные значения для разного сорта молекул. Уравнение (5.1.2) не выводится, оно устанавливается введением в уже известное уравнение Менделеева – Клапейрона двух поправок. Чтобы обосновать их введение заметим, что в уравнении (5.1.2) объем означает объем сосуда, в котором содержится один моль газа. В случае идеального газа, состоящего из материальных точек, весь этот объем доступен для движения молекул. В реальном газе сами молекулы занимают некоторую часть объема сосуда, и эта часть недоступна для всех других молекул. Эту часть объема следует вычесть из объема .