Основные параметры состояния рабочего тела

Основные параметры состояния рабочего тела

1. Удельный объем тела (v) представляет объем единицы его массы. В технической термодинамике за единицу массы принимают килограмм (кг), за единицу объема – кубический метр (м³). Следовательно, удельный объем равен объему в кубических метрах одного килограмма вещества:

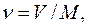м³/кг

Величина, обратная удельному объему представляет массу единицы объема и называется плотностью:

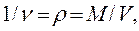кг/м³

2. Давление в международной системе единиц (СИ) измеряют в паскалях. Паскаль (Па) – давление, вызываемое силой в 1 ньютон (Н), равномерно распределенной по нормальной к ней поверхности площадью 1м². Во всех термодинамических уравнениях пользуются для измерения давления Па=Н/м², поэтому в формулы следует подставлять числовые значения давления только в этих единицах измерения. Для практических целей давление удобнее измерять в килопаскалях (кПа) и мегапасклях (МПа).

1кПа=10³ Па=10³ Н/м²; 1МПа=10⁶Па=10⁶Н/м²

Для измерения давления используют барометры, манометры и вакуумметры. Барометрами измеряют атмосферное давление, манометры служат для измерения давления выше атмосферного. В термодинамике параметром состояния рабочего тела является только абсолютное давление. Абсолютное давление определяется из соотношения:

Р_абс=Р_ман+В

где В– атмосферное (барометрическое) давление, Па. Вакуумметры служат для измерения давления ниже атмосферного. Абсолютное давление в этом случае находят из равенства:

Р_абс=В — Р_вак

Температурахарактеризует степень нагретости тела. Единицей термодинамической температуры является Кельвин (К) и обозначается — Т .

Термодинамическая температура также может быть выражена в градусах Цельсия (⁰С); она обозначается символом t. Температура таяния льда равна 273 К, что на 0,01⁰ ниже температуры тройной точки воды. Поэтому температура в градусах Цельсия определяется выражением:

t = Т – Т₀, ^ОС

где Т – абсолютная температура, выраженная в кельвинах; Т₀=273,15К.

Цена деления стоградусной шкалы Цельсия равна цене деления абсолютной шкалы Кельвина.

Термическое уравнение состояния рабочего тела

При постоянных давлениях и температуре единица количества ве-ва имеет всегда вполне определенный объем. Эту зависимость всегда можно выразить в виде функции связии давления p, удельного объема V и температуры Т.

F(p, V, T)=0

Это соотношение называется термическим уравнением состояния вещества. Три переменные p, V, T - параметры состояния. Если 2 из них известны, то третье можно определить через уравнение состояния

p=p(V, T)

V=V(p, T)

T=T(p, V)

Уравнение состояния может быть представлено в виде поверхности в пространстве с координатами p, V, T. Но в технике чаще используют кривые в плоскости 2х координат.

Для решения задач методами термодинамики необходимо знать уравнение состояния, однако оно должно быть получено опытным путем, т.к. конкретный вид уравнения зависит от индивидуальных свойств веществ.

Первый закон термодинамики

Первый закон термодинамики– изменение внутренней энергии системы при переходе из одного состояния в другое равно сумме количества теплоты, подведенной к системе из вне и работе внешних сил действующих на нее:∆U=Q+A.

Аналитические выражения:

Через внутреннюю энергию и работу: dq=du+pdV

Через энтальпию: dq=dh-Vdp

6. Уравнение состояния идеальных газов. Законы идеальных газов.

1. Закон Бойля – Мариотта устанав-т завис-ть между удельным объемом и абсолют. давлением ИГ в процессе при пост. темп-ре. «При постоянной температуре объем, занимаемый ИГ-ом, изм-ся обратно пропорционально его давлению» или «При пост. тем-ре произведение удельного объема на давление есть вел-на пост-ная». p·v = const. 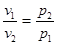(Т = const)

2. Закон Гей-Люссака устан-ет зав-сть между удельным объемом и абс.тем-рой при пост. давл-и. «При постоянном давлении объемы одного и того же количества идеального газа изменяются прямо пропорционально абсолютным температурам»

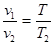при (р=const).«Если давление газа в процессе нагрева поддерживать неизменным, то объем газа при нагреве будет увеличиваться с ростом температуры» , при р=const, ρ · Т = const

где V₀ – объем газа при температуре 0º С; V – объем газа при температуре t º С; α- температурный коэффициент объемного расширения газа , α=1/273 К^-1.

3. Закон Шарля устан-ет зав-сть давления газа от его тем-ры при пост-ном удельном объеме (француз, 1737 г.).« При пост-ом объеме давление газа изменяется прямо пропорционально его абсол. температуре» р / Т = const, 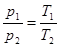, при v = const

4.Закон Авогадро: «При один-х тем-рах и давл-х в равных объемах различных ИГ содержится одинаковое количество молекул». Так как ρ=1/ v, то μ· v = const.

Уравнение состояния ИГ было выведено франц. Физиком Клапейроном в 1834 г. и связ-ет между собой основные параметры сост-я — давление,

Каждое из этих уравнений отличается от другого лишь тем, что относится к различным массам газа: первое — к М кг; второе—к 1 кг, третье— 1 кмолю газа.

7. Теплоемкость идеальных газов. Основные определения. Теплоемкост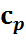и и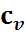

Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c.

c = Q / (mΔT).

Во многих случаях удобно использовать молярную теплоемкость C:

C = M · c,

где M – молярная масса вещества.

Определенная таким образом теплоемкость не является однозначной характеристикой вещества. Согласно первому закону термодинамики изменение внутренней энергии тела зависит не только от полученного количества теплоты, но и от работы, совершенной телом. В зависимости от условий, при которых осуществлялся процесс теплопередачи, тело могло совершать различную работу. Поэтому одинаковое количество теплоты, переданное телу, могло вызвать различные изменения его внутренней энергии и, следовательно, температуры.

Такая неоднозначность определения теплоемкости характерна только для газообразного вещества. При нагревании жидких и твердых тел их объем практически не изменяется, и работа расширения оказывается равной нулю. Поэтому все количество теплоты, полученное телом, идет на изменение его внутренней энергии. В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса. Обычно рассматриваются два значения теплоемкости газов: C_V – молярная теплоемкость в изохорном процессе (V = const) и C_p – молярная теплоемкость в изобарном процессе (p = const).

Политропные процессы.

Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной. В соответствии с сущностью понятия теплоёмкости , предельными частными явлениями политропного процесса являются изотермический процесс ( ) и адиабатный процесс ( ).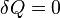

В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными (удельные теплоёмкости идеального газа при постоянном объёме и постоянном давлении соответственно равны 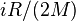и ( и не меняются при изменении термодинамических параметров).

Показатель политропы[править | править исходный текст]

Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде:

где р — давление, V — объем газа, n — «показатель политропы».

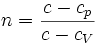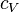. Здесь — теплоёмкость газа в данном процессе, и — теплоемкости того же газа, соответственно, при постоянном давлении и объеме.

В зависимости от вида процесса, можно определить значение n:

· Изотермический процесс: 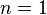, так как 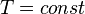, значит, по закону Бойля — Мариотта , и уравнение политропы вынуждено выглядеть так: .

· Изобарный процесс: , так как , и уравнение политропы вынуждено выглядеть так: .

· Адиабатный процесс: 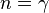(здесь — показатель адиабаты), это следует из уравнения Пуассона.

· Изохорный процесс: .

Цикл и теорема Карно

Понятие энтропии.

Ds=dq/T

Энтропия является функцией состояния, поэтому ее величина определяется параметрами состояния s=f (p,V,T).

В технической термодинамике используют лишь изменение энтропии в процессах, а не ее абсолютные значения.

Энтропия системы равна сумме энтропий отдельных подсистем или тел, входящих в систему.

16. Ts‑диаграмма идеального газа. Регенеративный цикл

Термические коэффициенты.

Если известно уравнение состояния, то каждый параметр состоя­ния может быть выражен как функция двух других параметров, т, е.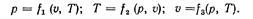

Полные дифференциалы этих величин будут:

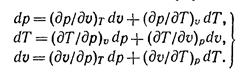
Частные производные при дифференциалах dp, dT и dv являются попарно величинами взаимно обратными и согласно правилам диффе­ренциального исчисления между ними имеется следующая зависи­мость:

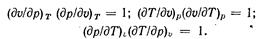
Следовательно, независимыми частными производными будут три из них. В качестве этих независимых производных выбирают следую­щие:

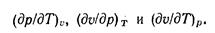
Эти частные производные входят в уравнение термических коэффи­циентов— сжатия, расширения и тепловой упругости, которые могут быть определены опытным путем.

Отношение частной производной (dV/dp) _т к объему V характери­зует скорость изменения объема с увеличением давления при постоян­ной температуре. Отношение называют изотермическим коэффициентом сжатия тела 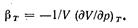(4-9)

Знак минус в правой части равенства поставлен для того, чтобы р_г получился положительной величиной, так как (dV/dp) _т всегда от­рицательна.

Отношение частной производной (dV/dT)_p к объему V характери­зует скорость изменения-объема при нагревании, если давление остает­ся постоянным. Это отношение называют коэффициентом термического расширения тела 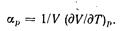(4-10)

Отношение частной производной (др/дТ)у к давлению р характе­ризует интенсивность изменения давления при увеличении темпера­туры, если объем тела остается постоянным.

Это отношение называют коэффициентом тепловой упругости «ли термическим коэффициентом давления 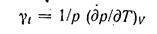(4-11)

Уравнения Максвелла

Уравнение Ван-дер-Ваальса

Как отмечалось ранее, при низких температурах и высоких давлениях уравнение Менделеева – Клапейрона для одного моля вещества дает существенные отклонения от значений, измеряемых на опыте.

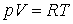
Были сделаны многочисленные попытки найти уравнение состояния для реального вещества, которое могло бы охватить, если не все состояния вещества, то хотя бы газообразное и жидкое. Из множества предложенных уравнений наибольшей известностью пользуется уравнение Ван-дер-Ваальса:

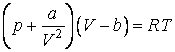
записанное для одного моля вещества. Для молей это уравнение имеет вид:

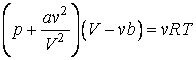
Постоянные a и b определяются экспериментально и имеют различные значения для разного сорта молекул. Уравнение (5.1.2) не выводится, оно устанавливается введением в уже известное уравнение Менделеева – Клапейрона двух поправок. Чтобы обосновать их введение заметим, что в уравнении (5.1.2) объем означает объем сосуда, в котором содержится один моль газа. В случае идеального газа, состоящего из материальных точек, весь этот объем доступен для движения молекул. В реальном газе сами молекулы занимают некоторую часть объема сосуда, и эта часть недоступна для всех других молекул. Эту часть объема следует вычесть из объема .

ДРОССЕЛИРОВАНИЕ ГАЗОВ

Процесс дросселирования

Процесс понижения дав­ления реального газа или пара при переходе через препятствие без со­вершения технической работы называется дроссели­рованием. При некоторых усло­виях в результате дросселирования снижается температура газа — этот эффект используют в холодильной технике. В тепловых двигателях при течении рабочего тела (реального газа или пара) по трубам с вентилями, клапанами или другими препятствия­ми происходит процесс дросселирова­ния, в результате которого снижается работоспособность рабочего тела, в связи с чем уменьшается коэффи­циент полезного действия двигателя.

Если процесс дросселирования протекает без обмена теплотой С ок­ружающей средой (т. е. адиабатно), то в процессе дросселирования эн­тальпия не изменяется.

Так как в процессах дросселирования изменение скорости очень мало, то им можно пренебречь. Та­ким образом, в результате дросселирования энтальпия газа не изменяется. Этот вывод получен на основании уравнения первого закона термодинамики и поэтому ОН справедлив как для реальных газов и паров, так и для капельных жидкостей.

При переходе газа или пара через диафрагму скорость его движения должна стать больше так как площадь проходного се­чения диафрагмы меньше проходного сечения канала. После диафрагмы скорость должна вновь уменьшиться так как площадь проходного сечения канала увеличивается. Если при этом выполняется условие равенства скоростей течения газа или пара в сечениях, то можно предположить, что в этих сечениях должны выровняться и давления. Однако в действительности p_L оказывается большим р_г. Это объясняется тем, что часть разности кинетических энергий движения пото­ка через диафрагму и после нее преобразуется в теплоту, од­нако ее не хватает для повышения давления текущего вещества в се­чении.

Основные параметры состояния рабочего тела

1. Удельный объем тела (v) представляет объем единицы его массы. В технической термодинамике за единицу массы принимают килограмм (кг), за единицу объема – кубический метр (м³). Следовательно, удельный объем равен объему в кубических метрах одного килограмма вещества:

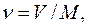м³/кг

Величина, обратная удельному объему представляет массу единицы объема и называется плотностью:

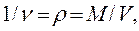кг/м³

2. Давление в международной системе единиц (СИ) измеряют в паскалях. Паскаль (Па) – давление, вызываемое силой в 1 ньютон (Н), равномерно распределенной по нормальной к ней поверхности площадью 1м². Во всех термодинамических уравнениях пользуются для измерения давления Па=Н/м², поэтому в формулы следует подставлять числовые значения давления только в этих единицах измерения. Для практических целей давление удобнее измерять в килопаскалях (кПа) и мегапасклях (МПа).

1кПа=10³ Па=10³ Н/м²; 1МПа=10⁶Па=10⁶Н/м²

Для измерения давления используют барометры, манометры и вакуумметры. Барометрами измеряют атмосферное давление, манометры служат для измерения давления выше атмосферного. В термодинамике параметром состояния рабочего тела является только абсолютное давление. Абсолютное давление определяется из соотношения:

Р_абс=Р_ман+В

где В– атмосферное (барометрическое) давление, Па. Вакуумметры служат для измерения давления ниже атмосферного. Абсолютное давление в этом случае находят из равенства:

Р_абс=В — Р_вак

Температурахарактеризует степень нагретости тела. Единицей термодинамической температуры является Кельвин (К) и обозначается — Т .

Термодинамическая температура также может быть выражена в градусах Цельсия (⁰С); она обозначается символом t. Температура таяния льда равна 273 К, что на 0,01⁰ ниже температуры тройной точки воды. Поэтому температура в градусах Цельсия определяется выражением:

t = Т – Т₀, ^ОС

где Т – абсолютная температура, выраженная в кельвинах; Т₀=273,15К.

Цена деления стоградусной шкалы Цельсия равна цене деления абсолютной шкалы Кельвина.