Синтез разомкнутой САР с ПИ – регулятором

Исходя из вышеизложенного, для определения устойчивости по критерию Найквиста необходимо построить амплитудно – фазо - частотную характеристику разомкнутой системы автоматического регулирования уровня.

В общем виде передаточную функцию разомкнутой САР с регулятором можно найти по формуле:

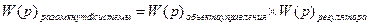. (8)

Пример: передаточная функция разомкнутой системы с ПИ- регулятором примет вид:

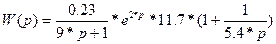(9)

Синтез разомкнутой САР с ПИД – регулятором

Передаточная функция разомкнутой системы с ПИД – регулятором записывается по алгоритму, описанному выше.

Пример: Для получения передаточной функции разомкнутой САР с ПИД- регулятором воспользуемся формулой 8:

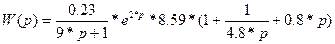(10)

Оценка устойчивости САР

Запас устойчивости по амплитуде и по фазе системы с ПИ- регулятором

По критерию Найквиста проанализируем, является ли устойчивой САР. Для этого в Маткаде построим АФЧХ разомкнутой системы. Полученные графики позволят также определить запасы устойчивости системы по фазе и по амплитуде.

Пример: Построение АФЧХ разомкнутой системы с ПИ- регулятором в Маткаде показано на рисунке9.

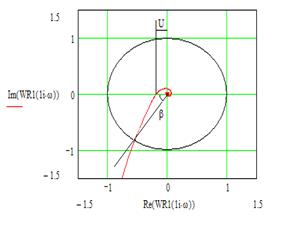
Рисунок 9 - АФЧХ разомкнутой системы с ПИ – регулятором

По АФЧХ разомкнутой системы с ПИ – регулятором можно сделать вывод, что замкнутая система с ПИ- регулятором является устойчивой по критерию Найквиста. Проведя дополнительные построения, определим: запас устойчивости по амплитуде составляет А=1/U=4, по фазе запас устойчивости Q=50⁰.

7.3.2 Запас устойчивости по амплитуде и фазе системы с ПИД –

Регулятором

Пример построения АФЧХ разомкнутой системы с ПИД – регулятором показан на рисунке 10.

Рисунок 10 – АФЧХ разомкнутой системы с ПИД –регулятором.

Из рисунка 10 видно, что, по критерию Найквиста замкнутая система с ПИД- регулятором является устойчивой. Проведя дополнительные построения, определим: запас устойчивости по амплитуде составляет А=1/U=0,33, по фазе запас устойчивости Q=40⁰.

Определение показателей качества управления

Замкнутой САР

Различают 4 группы критериев качества регулирования:

¾ Критерии точности - используют величину ошибки в различных типовых режимах.

¾ Критерии величины запаса устойчивости - оценивают удаленность САР от границы устойчивости.

¾ Критерии быстродействия - оценивают быстроту реагирования САР на появление задающего и возмущающего воздействий.

¾ Интегральные критерии - оценивают обобщенные свойства САР: точность, запас устойчивости, быстродействие.

Существует два основных подхода к оценке качества:

1. Первый использует информацию о временных параметрах системы: h(t), w(t); расположение полюсов и нулей ПФ замкнутой системы F(p).

2. Второй использует информацию о некоторых частотных свойствах системы: полоса пропускания; относительная высота резонансного пика; и т.д.

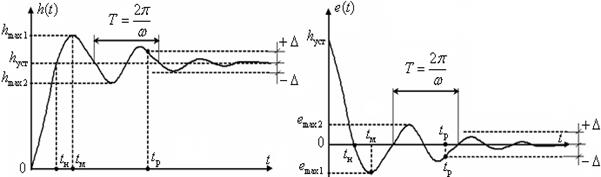
Рисунок 11 – Переходная функция

Рисунок 12 – Весовая функция

Рассмотрим прямые оценки качества переходных процессов, показанные на рисунках 11 и 12:

1. Установившееся значение выхода, определяющее статическую точность системы:

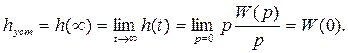(11)

2. – время переходного процесса, определяющее быстродействие системы. Оно определяется из соотношения

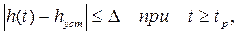(12)

где 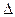- заданная малая величина, характеризующая точность системы.

предварительно задается в процентах от установившегося значения , где нет определенных требований – принимают .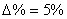

3. 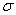– перерегулирование – максимальное отклонение от установившегося значения, выраженное в относительных единицах или процентах

или (13)

Обычно требования по перерегулированию составляют , иногда к качеству процессов может быть предъявлено требование 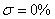, на пример в системах позиционирования манипуляторов промышленных роботов.

4. 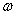– частота колебаний

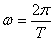(14)

где 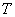– период колебаний для колебательных процессов.

5. – это число полных колебаний, которое имеет 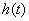или за время регулирования . Этот параметр определяется как число выбросов, для которых

(15)

Обычные требования по числу колебаний , в некоторых системах накладывают ограничение на колебательность , на пример, в системах с существенным люфтом в механических передачах.

6. 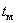– время достижения первого максимума.

7. 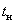– время нарастания переходного процесса, время от начала переходного процесса до момента первого пересечения графиком линии установившегося значения.

8. 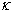– декремент затухания, равный отношению модулей двух смежных перерегулирований

9. . (16)