Тема: Выборочное наблюдение.

Цель работы: Получить навыки проведения и обработки выборочного исследования.

План:

1. Методы обеспечения репрезентативности выборки.

2. Группировка выборочной информации.

3. Расчет выборочной средней и выборочной доли.

4. Расчет предельной ошибки выборки.

Задание:

1. Вывести формулу необходимой численности выборки для заданных пределов генеральной средней повторного отбора.

2. Вывести формулу необходимой численности выборки для заданных пределов генеральной средней бесповторного отбора.

3. Вывести формулу необходимой численности выборки для заданных пределов генеральной доли повторного отбора.

4. Вывести формулу необходимой численности выборки для заданных пределов генеральной доли бесповторного отбора.

Теоретический материал.

Под выборочным понимается метод статистического исследования, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой ее части на основе положений случайного отбора. Обычно это до 5 – 10%, реже до 15 – 25%. В основе выбора единиц для обследования положены принципы равных возможностей попадания в выборку каждой единицы генеральной совокупности. Это исключает тенденциозные ошибки и делает выборку репрезентативной.

Поскольку сама генеральная совокупность состоит из единиц с варьирующими признаками, то состав выборочной совокупности может в той или иной мере отличаться от состава генеральной. Это расхождение составляет ошибку выборки.

Применяя выборочный метод в экономических расчетах, обычно используют два основных вида обобщающих показателей: относительную величину альтернативного признака и среднюю величину количественного признака.

Для генеральной совокупности эти величины называются «генеральная средняя», (обозначается - 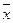) и генеральная доля (обозначается – р).

Для выборки – выборочная средняя (обозначается - 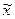), выборочная доля (обозначается - w). Выборочная доля или частость определяется из отношения числа выбранных единиц, обладающих изучаемым признаком, к численности выборки: .

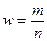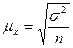Возможные расхождения между характеристиками выборочной и генеральной совокупности измеряются средней ошибкой выборки m. В математической статистике доказывается, что значения средней ошибки определяются по формулам: - ошибка средней величины, 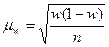- ошибка выборочной доли. Следует помнить, что отбор может быть повторным и бесповторным. Сущность повторного отбора состоит в том, что опрошенная единица после фиксации значения возвращается в генеральную совокупность и может быть опрошена снова. Вероятность быть опрошенной сохраняется постоянной у всех вариант.

При бесповторном отборе численность генеральной совокупности N в ходе выборки сокращается, вероятность быть опрошенными у оставшихся элементов возрастает, ошибки выборки уменьшаются на долю неопрошенных вариант. Ошибки бесповторного отбора рассчитываются по формулам:

, .

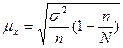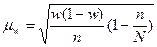Такие ошибки можно гарантировать не с абсолютной достоверность††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††. Вероятность суждения можно повысить, если расширить пределы отклонений, приняв в качестве меры среднюю ошибку выборки, увеличенную в t раз.

В практических экономических расчетах обычно ограничиваются значениями t, не превышающими двух-трех единиц. При этом выбор той или иной доверительной вероятности зависит от того, с какой степенью достоверности требуется гарантировать результаты выборочного обследования. Приведем часть таблицы распределения вероятностей:

Вероятность F(t)	0.000	0.0797	0.3829	0.6827	0.8664	0.9545	0.9876	0.9907	0.9973	0.99994
Кратность ошибки t	0.0	0.1	0.5	1.0	1.5	2.0	2.5	2.6	3.0

Предельные ошибки выборки рассчитываются по формулам:

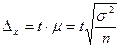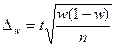, - - для повторного,

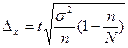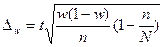, - для бесповторного отборов.

, .

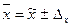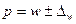Обратная задача выборочного наблюдения состоит в определении оптимальной численности выборки при условии, что заданы границы ошибок выборки и определен размер дисперсий. Формулы расчета численности студентам предлагается вывести самим.

Значения предельной ошибки и кратности ошибки определяются как задачами, стоящими перед исследователем, так и природой изучаемого явления. Чем более достоверные результаты требуется получить, тем большую вероятность необходимо задать. С увеличением допустимой ошибки уменьшается необходимый объем выборки и наоборот. Вариация признака (дисперсия) существует объективно, независимо от исследователя, но к началу выборочного наблюдения она неизвестна. Приближенно дисперсию определяют следующими способами:

1) берут из предыдущих исследований;

2) по правилу «трех сигм» общий размах вариации укладывается в 6 сигм (R @ 6s, отсюда s @ R/6). Для большей точности размах делят на 5;

3) Если хотя бы приблизительно известна средняя величина изучаемого признака, то s @ х_{ар.средн.}/3;

4) при изучении альтернативного признака, если нет даже приблизительных сведений о доле единиц, обладающих заданным значением этого признака, берется максимально возможная величина дисперсии, равная 0,25.

При серийном отборе общее число отбираемых единиц делится на количество групп.

При стратифицированном отборе число наблюдений по каждой группе берется пропорционально структуре генеральной совокупности:

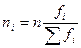, где n – численность выборки, n_i – число выбираемых элементов из одной подгруппы.

ЗАДАЧИ:

Задача 1.

На основе выборочного обследования в отделении связи города предполагается определить долю писем частных лиц в общем объеме отправляемой корреспонденции. Никаких предварительных данных об удельном весе этих писем в общей массе отправляемой корреспонденции не имеется.

Размер допустимой (предельной) ошибки – 1% или 0,01; принятая вероятность 0,95.

Задача 2.

На предприятии в порядке случайной бесповторной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за октябрь:

Месячный доход, руб.	600 - 1000	1000 - 1400	1400 – 1800	1800 – 2200
Число рабочих

Определить:

1) Среднемесячный размер дохода у работников данного предприятия, гарантируя результат с вероятностью 0,997.

2) Долю рабочих предприятия, имеющих месячный доход 1400 руб. и выше, гарантируя результат с вероятностью 0,954.

3) Необходимую численность выборки при определении среднего месячного дохода работников предприятия, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 50 руб.

По условию задачи известны:

При вероятности Р=0,954; t=2;

1) 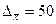руб.; s =93184.

4) Необходимую численность выборки при определении доли рабочих с размером месячного дохода 1400 руб. и выше, чтобы с вероятностью 0,954 предельная ошибка не превышала 4%.

По условию задачи известны:

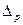=2%, или 0,02; при вероятности Р = 0,954; t = 2;

w=0,28.

Задача 3.

Операция шлифования при обработке детали № 312 производится в цехе на трех станках. Для определения процента брака для всей партии продукции, выработанной за день, проведено расслоение 10%-ной выборки. Отбор деталей из выработки каждого станка – случайный бесповторный; объем выработки пропорционален размеру выпуска. На первом станке было обработано 1700 деталей, на втором – 1000, на третьем –1800. Число забракованных деталей в выборке: по первому станку –2, по второму – 3, по третьему – 3.

Определить:

1) Доверительные интервалы, в которых с вероятностью 0,95 заключен процент брака для всей партии продукции.

2) Вероятность того, что процент брака для всей партии продукции отличается от полученного по выборке не более чем на 0,6%.

Для решения второго задания известна допустимая ошибка 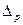=0,6%, или 0,006.

Задача 4.

При контрольной проверке качества апельсинов проведена 10%-ная серийная выборка. Из партии, содержащей 50 ящиков апельсинов (вес ящиков одинаков), методом механического отбора взято 5 ящиков. В результате сплошного обследования находящихся в ящике апельсинов получили данные об удельном весе бракованных апельсинов. Результаты следующие:

№ ящика, попавшего в выборку
Удельный вес бракованной продукции	1,2	1,8	2,0	1,0	1,5

Требуется с вероятностью 0,95 установить доверительные интервалы удельного веса бракованной продукции для всей партии апельсинов.

При вероятности Р=0,95; t = 1,96.

Задача 5.

Из партии электроламп произведена малая выборка (отбор случайный, бесповторный) для определения продолжительности службы ламп. Результаты выборки следующие:

№ лампы
Срок горения, час.

На основе приведенных данных требуется:

1) Определить доверительные интервалы, в которых заключена средняя продолжительность службы ламп для всей партии, гарантируя результат с вероятностью 0,99.

2) Определить вероятность того, что средний срок службы ламп для всей партии отличается от полученного по выборке не более чем на 40 часов.

Задача 6.

Обработка детали № 427производится в цехе на двух однотипных станках. При выборочном наблюдении (механический отбор единиц) были зарегистрированы следующие затраты на обработку одной детали:

Затраты времени на одну деталь, мин	Число деталей
Станок № 1	Станок № 2
1,5 - 2,5		-
2,5 - 3,5
3,5 - 4,5
4,5 - 5,5
Итого:

На основе приведенных данных определить, существенно ли расхождение в затратах времени на обработку одной детали для этих двух станков, гарантируя результат с вероятностью 0,95 [1,129].

Задача 7.

Из общего количества рабочих предприятия была проведена 30%-ная случайная бесповторная выборка с целью определения затрат времени на проезд к месту работы. Результаты выборки следующие:

Затраты врем. на проезд, мин.	До 30	30 - 40	40 - 50	50 - 60	60 – 70
Число рабочих

Определить: 1) средние затраты времени на проезд к месту работы у рабочих данного предприятия, гарантируя результат с вероятностью 0,997;

3) долю рабочих предприятия, у которых затраты времени на проезд к месту работы составляют 60 мин. И более, гарантируя результат с вероятностью 0,954.

Задача 8.

Выходной контроль качества поступающих на предприятие комплектующих изделий, осуществляемый в порядке механической выборки, дал результаты:

Отклонение размера изделия от принятого по ГОСТу, %	Число изделий
От -2,0 до -3,0 -1,0 до –2,0 0,0 до -1,0 1,0 до 0,0 2,0 до 1,0 3,0 до 2,0 4,0 до 3,0 5,0 до 4,0

Определить: 1) пределы значений среднего отклонения размера изделий от стандарта по ГОСТу с вероятностью 0,997;

3) пределы долей изделий с отрицательным отклонением в общей совокупности изделий с вероятностью 0,954.

Задача 9.

Произведен пропорциональный отбор рабочих со сдельной и повременной системами оплаты труда для изучения показателей выполнения сменного задания. Отбор единиц в каждой группе бесповторный. Выборка дала следующее распределение численности рабочих по проценту выполнения норм выработки:

Группы рабочих по оплате труда	Группы рабочих по проценту выполнения сменного задания	Итого рабочих
До 100	100-120	120-140	140 и выше
Рабочие – сдельщики
Рабочие – повременщики
Итого:

Определить:

1) Доверительные интервалы, в которых с вероятностью 0,954 заключен средний процент выполнения сменного задания для всех рабочих предприятия;

2) Возможные пределы доли рабочих, выполняющих сменное задание не менее чем на 120% (с вероятностью 0,954);

3) Необходимую численность выборки при определении доли рабочих, выполняющих сменное задание не менее чем на 120%, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 3%.

Задача 10.

В ООО «Прогресс» работает 3000 человек. Методом случайной бесповторной выборки обследовано 1000 человек, из которых 820 выполняли и перевыполняли дневную норму выработки.

Определить: 1) долю рабочих, не выполняющих норму выработки, по данным выборочного обследования;

2) долю всех рабочих акционерного общества, не выполняющих норму (с вероятностью 0,954).

Задача 11.

Из партии изготовленных изделий общим объемом 2000 единиц проверено посредством механической выборки 30% изделий, из которых бракованными оказались 12 изделий.

Определить:

1) долю бракованных изделий по данным выборки;

2) пределы, в которых находится процент бракованных изделий, для всей партии (с вероятностью 0,954).

Задача 12.

По данным выборочного обследования 10000 пассажиров пригородного сообщения средняя дальность поездки пассажира составила 35,5 км, а среднее квадратическое отклонение – 16,0 км.

Определить:

1) пределы средней дальности поездки пассажиров с вероятностью 0,954;

2) как изменится предельная ошибка выборки, если вероятность будет принята равной 0,997?

Задача 13.

Хронометраж работы станочника дал следующие результаты:

Затраты времени на изготовление одной детали, сек.	50 - 60	60 - 70	70 - 80	80 - 90	90 - 100	Итого:
Количество деталей, шт.

Определить:

1) средние затраты времени на обработку одной детали по данным наблюдения;

3) предельную ошибку выборки с вероятностью 0,954, учитывая, что речь идет о массовом производстве, т.е. выборка производится из генеральной совокупности бесконечно большого объема.

Задача 14.

В механическом цехе завода в порядке малой выборки изучались фотографии рабочего дня 10 рабочих. Время непроизводительной работы и перерывов, зависящих от рабочего и по организационно-техническим причинам, для обследования рабочих составило: 52, 48, 60, 46, 62, 54, 51, 49, 55, 53 мин.

Определить:

1) доверительные пределы, в которых находится среднее время производительной работы и перерывов для всех рабочих цеха, гарантируя результат с вероятностью 0,99;

2) вероятность того, что среднее время непроизводительной работы и перерывов всех рабочих цеха отличалось от полученного по выборке не более, чем на 3 мин.