Дискретные случайные величины
1.
| x | ||||
| P | 0,512 | 0,384 | 0,096 | 0,008 |
Mx= 0,6 D x= 0,48
2.
| x | |||
| P | 0,36 | 0,48 | 0,16 |
3.
| Значения | |||
| Вероятность | 0,02 | 0,26 | 0,72 |
4. 
5.
| Значения | |||||
| Вероятности | 1/16 | 1/4 | 3/8 | 1/4 | 1/16 |
6.
| x | |||||
| P | 0,3969 | 0,4284 | 0,1534 | 0,0204 | 0,0009 |
Mx= 0,8 D x= 0,6
7.
| Значения | |||
| Вероятности | 0,512 | 0,384 | 0,104 |
8.
| Значения | ||||
| Вероятности | 0,5 | 0,3 | 0,15 | 0,05 |
Mx= 1,75 D x= 0,79
9.
| Значения | ||||
| Вероятности |  |  | 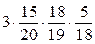 |  |
Mx= 2,25 D x= 2,81
10.
| Значения | ||||
| Вероятности | 0,4 | 0,3 | 0,2 | 0,1 |
Mx= 2; D x= 1; P{x>2}=0,3.
11.
| Значения | ||||
| Вероятности | 0,2 | 0,16 | 0,128 | 0,512 |
Mx= 2,952; P{x>2}=0,64.
12.
| Значения | |||
| Вероятности | 0,5 | 0,48 | 0,02 |
13. 40. 14. 1,5;  15. 5; 0,128; 0,488.
15. 5; 0,128; 0,488.
16.
| Значения | -1 | ||
| Вероятности | 0,5 | 0,3 | 0,5 |
17. 0,027; 1,42.
Непрерывные случайные величины
1.
а) с=2 б) 
г) Mx= 2/3 D x= 1/18
д) P(x<M x)= 4/9 , 

2. c=1; 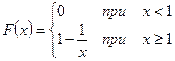
Mx= ∞ D x=∞; P{ x<∞}= 0.
3. c=1; 
Mx= 2 D x= 1; P{ x<Mx}= 1 – e-1;
P{ x>Mx+0,1}= e-1,1
4. c=1/2; 
5. Mx=2; Dx= 4/3.
6. c= 1/9; 
7. 1. Нет P{ x<310}= 0,977. Надо записать 311б65 тонны.
8. 0,023; призывать тех, у кого рост больше 192,8 см.
9. 0,0668; посылать ревизора, если стоимость больше 1828 руб.
10. 0,0062; отправлять в ремонт при расходе, превышающем
19,66 кг.
11.  . 12. Mx= 1,5; Dx= 100; x0,96=19
. 12. Mx= 1,5; Dx= 100; x0,96=19
13. Mx= 1; Dx= 3; x0,96=3,88; x0,5=1.
14. Mx= – 1; P= 0,75. 15. 0,32; s=0,036
16. 0,477; 0,954 17. s» 0,01 18. »0,023
19. 1 – e-2; - ln 0,2 20. 1 – e-0,75
21. a= 1/4; P(1£x£ 2)= ½.
22. 22. A= 1/2; B=1/p;

23. 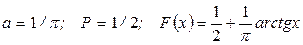
24. Mx= 0; D x= 1/16.
25. 
26. mx=435; 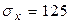
1. x : 0 1 y : - 1 0 1
P : 0,45 0,55 P : 0,25 0,40 0,35
Mx= 0,55; My= 0,10
2.
| y / x | |||
| 1/5 | 1/10 | 1/5 | |
| 1/15 | 1/30 | 1/15 | |
| 2/15 | 1/15 | 2/15 |
3. Mx= 2,1; My= 0,9; Dx=Dy= - K xy =0,63.
4.
| Значения x1 | |||
| Вероятности | 0,38 | 0,34 | 0,28 |
| Значения x2 | ||||
| Вероятности | 0,08 | 0,37 | 0,29 | 0,26 |
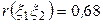
6.
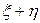 | |||||
| Р | 1/6 | 11/24 | 1/4 | 1/24 | 1/12 |
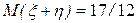
7. 49,375; 0,54 8. M(h) = - 6; D(h)= 73; r=0,5
9. 

11. Нет. 12. 
13. 
14. 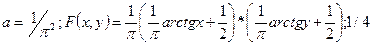
15. 
16. 
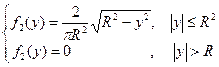
17. 

18. 
19. 
20. 
21. 1. 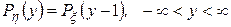
2. 
3. 
4. 
5. 
6. 
22. 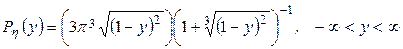
23. 
24. 
25. 
26. 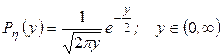
28. Mx=1, Dx= 1, My= 2, Dy =20.
29. MR=2R/3, DR=R2/18
30. 2s2. 31.  .
.
32. 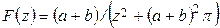
33. 
34.  . 35.
. 35. 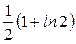
1. P2 может, остальные нет.
2. 
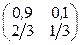
3. 
4. Состояния: 1 – нет работы, 2 – первый день работы над мотором М2, 3 – второй день работы над мотором М2, 4 – работа над мотором М1
а) 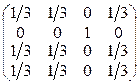 б)
б) 
5. 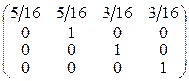
6.

7.
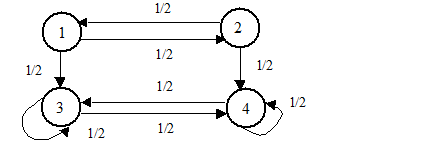
8. а) 0,39; б) 0,547;
9. а) 5/9; б) 41/72.
10. а)  б)
б) 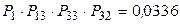
в) 
11. 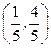 12.
12. 
13. Стационарное распределение  руб.
руб.
14. а) 0,6; б) 0,43;
в) стационарное распределение  . Искомая вероятность
. Искомая вероятность
11/36.
15. a)  в)
в)  ; г) (0,4; 0,2; 0,4).
; г) (0,4; 0,2; 0,4).
16. 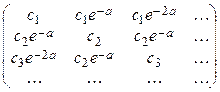
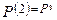 . Например,
. Например, 
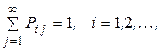 откуда
откуда
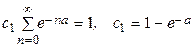

2. 0,4; 0,15; 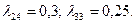 4.
4. 
5. 3e-2. 6. 2e-lt – e-2lt= 2e-2 – e-4.
7.  . 8.
. 8. 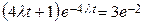
9. 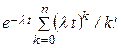
10. Система уравнений для вероятностей 

Откуда 
1. e-0,5. 2. ln 2/2. 3. 0,5 суток. 4. 1/e
6. 2 мин. 7. 3e-2. 8. e-2. 9. 3 минуты. 10. e-3.
3. а)  б)
б) 
в) 
4.  5.
5. 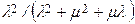
6. 
7. 
9. 
10. Для А существуют, для В не существуют; 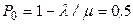 .
.
11. 5 заданий в день (  ). 12. 1/3.
). 12. 1/3.
1. 2,65; 3. 3. 2,08; 0,1. 4. » 0,05 мин.; 1,5; » 0,08.
5. 1 минута. 6. 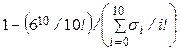
7. 2/3. 8. » 1,87. 9. » 1,2, »0,3.
ПРИЛОЖЕНИЕ
Значения функции Лапласа 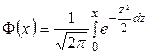
| x | ||||||||||
| 0,0 | 0,00000 | 03 188 | ||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | 17 724 | |||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | ||||||||||
| 1,1 | ||||||||||
| 1,2 | 38 686 | |||||||||
| 1,3 | 41 149 | |||||||||
| 1,4 | 42 220 | |||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | 46 327 | |||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | ||||||||||
| 2,1 |
| x | ||||||||||
| 2,2 | ||||||||||
| 2,3 | 49 036 | |||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | 49 674 | |||||||||
| 2,8 | ||||||||||
| 2,9 |
| x | 3,0 | 3,5 | 4,0 | 5,0 |
| Ф(х) | 0,49865 | 0,49977 | 0,499968 | 0,49999997 |
Профессор, д.т.н. Борис Яковлевич Рябко
СБОРНИК ЗАДАЧ
ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ И
ОСНОВАМ ТЕОРИИ МАССОВОГО
ОБСЛУЖИВАНИЯ
Редактор: А.О. Ахметов
Корректор: Д.С.Шкитина
________________________________________________________
Подписано в печать , формат бумаги 62х84/16, отпечатано на ризографе, шрифт №10, изд.л. 5,3 , заказ № , тираж 250, СибГУТИ 630102, Новосибирск, ул.Кирова, 86.
