Теорема сложения скоростей при составном движении точки.
| Формулировка теоремы и векторное уравнение | Графическое нахождение 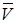 Из векторного уравнения Из векторного уравнения | Аналитическое нахождение 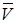 из векторного уравнения из векторного уравнения |
Абсолютная скорость 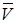 точки равна векторной сумме переносной ско-рости точки равна векторной сумме переносной ско-рости  точки и отно-сительной скорости точки и отно-сительной скорости  точки: точки:  . (1) . (1) | Находим  , ,  и в соответствии с уравнением (1) строим векторный параллелограмм (или треугольник). и в соответствии с уравнением (1) строим векторный параллелограмм (или треугольник).  или или  Если построение выполнено в масштабе, то из чертежа находим модуль V. Можно также вычислить V, используя известные стороны и углы построенных треугольников и формулы тригонометрии (например, теорему косинусов). Если построение выполнено в масштабе, то из чертежа находим модуль V. Можно также вычислить V, используя известные стороны и углы построенных треугольников и формулы тригонометрии (например, теорему косинусов). | Находим  , ,  ; выбираем оси координат и уравнение (1) проектируем на эти оси: ; выбираем оси координат и уравнение (1) проектируем на эти оси:  Далее находим модуль Далее находим модуль  и направление вектора и направление вектора 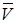 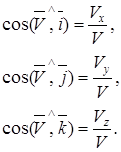 |
Теорема сложения ускорений при составном движении точки (теорема Кориолиса).
| Формулировка теоремы и вектор- ное уравнение | Графическое нахождение  из векторного урав-нения из векторного урав-нения | Аналитическое нахождение  из векторного уравнения из векторного уравнения | Ускорение Кориолиса |
Абсолютное ускорение  точки в случае, когда переносное движе-ние точки не по-ступательное, равно векторной сумме переносного уско-рения точки в случае, когда переносное движе-ние точки не по-ступательное, равно векторной сумме переносного уско-рения 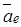 точки, относительного ускорения точки, относительного ускорения  точки и ускорения Корио-лиса точки и ускорения Корио-лиса  : :  . (1) В случае, когда переносное движе-ние точки – посту-пательное, . (1) В случае, когда переносное движе-ние точки – посту-пательное,  , и , и  . . | Находим 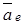 , , 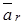 , ,  . Выбираем мас-штаб и в соответ-ствии с уравнением (1) строим век-торный многоуголь-ник. Вектор, прове-денный из начала первого в конец последнего вектора, дает абсолютное ускорение . Выбираем мас-штаб и в соответ-ствии с уравнением (1) строим век-торный многоуголь-ник. Вектор, прове-денный из начала первого в конец последнего вектора, дает абсолютное ускорение  точки. точки. 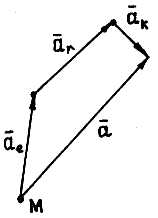 | Находим  , , 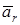 , ,  . Выбираем оси ко-ординат и проекти-руем уравнение (1) на эти оси: . Выбираем оси ко-ординат и проекти-руем уравнение (1) на эти оси:  Далее находим модуль Далее находим модуль  и направление вектора и направление вектора 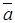  |  ; модуль ; модуль  , где , где  , ,  – модуль переносной угловой скорости, – модуль переносной угловой скорости,  – модуль относительной скорости точки. Определить направление – модуль относительной скорости точки. Определить направление  можно двумя способами. 1) Правило векторного произведения: вектор можно двумя способами. 1) Правило векторного произведения: вектор  направлен перпендикулярно плоскости перемножаемых векторов направлен перпендикулярно плоскости перемножаемых векторов 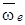 и и  , в ту сторону, , в ту сторону, |
 | откуда кратчайший по-ворот от вектора 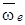 к вектору к вектору  выглядит происходящим против хода часовой стрелки. 2) Правило Жуковского: составляющую вектора выглядит происходящим против хода часовой стрелки. 2) Правило Жуковского: составляющую вектора  , которая перпенди-кулярна вектору , которая перпенди-кулярна вектору 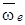 , надо повернуть на , надо повернуть на  в сторону переносного вращения – получим вектор в сторону переносного вращения – получим вектор  . . |
Рассмотрим два типовых примера (в примере К3а ось переносного вращения перпендикулярна пластине, в примере К3б – лежит в ее плоскости).
Пример K3a. Пластина OEAB1D (ОЕ = OD, рис. К3а) вращается вокруг оси, проходящей через точку О перпендикулярно плоскости пластины, по закону j = f1(t) (положительное направление отсчета угла j показано на рис. К3а дуговой стрелкой). По дуге окружности радиуса R движется точка В по закону  (положительное направление отсчета координаты s на траектории – от A к В).
(положительное направление отсчета координаты s на траектории – от A к В).
 Рис. К3а. Рис. К3а. | Дано: R = 0,5 м, j = t2- 0,5t3, s = pRcos(pt/3) (j – в радианах, s – в метрах, t – в секундах). Определить: абсолютную скорость Vабс и абсолютное ускорение аабс в момент времени t1 = 2 с. |
Решение. Рассмотрим абсолютное движение точки В как сложное, считая ее движение по дуге окружности относительным, а вращение пластины – переносным движением (подвижные оси B1xy связаны с пластиной). Тогда абсолютная скорость  и абсолютное ускорение
и абсолютное ускорение 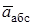 точки найдутся по формулам:
точки найдутся по формулам:
 (1)
(1)
где учтено,что
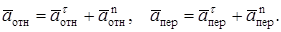
Определим все, входящие в равенства (1) величины.
1. Относительное движение (мысленно остановим пластину). Это движение задано естественным способом (см. задачу К1б). Закон движения точки по траектории:
 (2)
(2)
Сначала установим, где будет находиться точка В на дуге окружности в момент времени t1. Полагая в уравнении (2) t1 = 2 с, получим
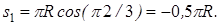
Тогда 
Знак минус свидетельствует о том, что точка В в момент t1 = 2 с находится справа от точки А. Изображаем ее на рис. К3а в этом положении (точка B1).
Теперь находим числовые значения 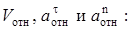

где  - радиус кривизны относительной траектории, равный радиусу окружности R. Для момента времени t1 = 2с, учитывая, что R = 0,5 м, получим
- радиус кривизны относительной траектории, равный радиусу окружности R. Для момента времени t1 = 2с, учитывая, что R = 0,5 м, получим
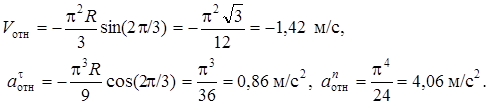 (3)
(3)
Знаки показывают, что вектор  направлен в сторону положительного отсчета координаты s, а вектор
направлен в сторону положительного отсчета координаты s, а вектор  в противоположную сторону; вектор
в противоположную сторону; вектор  направлен к центру С окружности. Изображаем все эти векторы на рис. КЗа.
направлен к центру С окружности. Изображаем все эти векторы на рис. КЗа.
2. Переносное движение (мысленно остановим точку на пластине). Это движение (вращение) происходит по закону  (см. задачу К2). Найдем угловую скорость w и угловое ускорение e переносного вращения:
(см. задачу К2). Найдем угловую скорость w и угловое ускорение e переносного вращения:

и при t1 =2 с

 (4)
(4)
Знаки указывают, что в момент t1 =2 с направления w и e противоположны направлению положительного отсчета угла j; отметим это на рис. К3а соответствующими стрелками.
Для определения  и
и  найдем сначала расстояние h1 = ОВ1 точки В1от оси вращения О. Из рисунка видно, что h1 =
найдем сначала расстояние h1 = ОВ1 точки В1от оси вращения О. Из рисунка видно, что h1 =  Тогда в момент времени t1 = 2 с, учитывая равенства (4) , получим
Тогда в момент времени t1 = 2 с, учитывая равенства (4) , получим


 (5)
(5)
Изображаем на рис. КЗа векторы  и
и  с учетом направления
с учетом направления  и
и  и вектор
и вектор  (направлен к оси вращения).
(направлен к оси вращения).
3. Ускорение Кориолиса. Модуль ускорения Кориолиса определяем по формуле 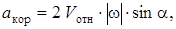 где a – угол между вектором
где a – угол между вектором  и осью вращения (вектором
и осью вращения (вектором  ). В нашем случае этот угол равен 90°, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор
). В нашем случае этот угол равен 90°, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор  . В момент времени t1= 2 с, учитывая, что в этот момент
. В момент времени t1= 2 с, учитывая, что в этот момент  и
и 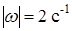 , получим
, получим
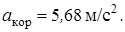 (6)
(6)
Направление  найдем по правилу Н.Е.Жуковского: так как вектор
найдем по правилу Н.Е.Жуковского: так как вектор  лежит в плоскости, перпендикулярной оси вращения, то повернем его на 90° в направлении
лежит в плоскости, перпендикулярной оси вращения, то повернем его на 90° в направлении  , т.е. по ходу часовой стрелки. Изображаем
, т.е. по ходу часовой стрелки. Изображаем  на рис. К3а. (Иначе направление
на рис. К3а. (Иначе направление  можно найти, учитывая, что
можно найти, учитывая, что 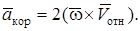 ) Изображаем вектор
) Изображаем вектор  на рис. К3а.
на рис. К3а.
Таким образом, значения всех входящих в правые части равенств (1) векторов найдены и для определения 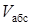 и
и 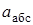 остается только сложить эти векторы. Произведем это сложение аналитически.
остается только сложить эти векторы. Произведем это сложение аналитически.
4. Определение 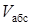 . Проведем координатные оси В1ху (см. рис. К3а) и спроектируем почленно обе части равенства
. Проведем координатные оси В1ху (см. рис. К3а) и спроектируем почленно обе части равенства  на эти оси. Получим для момента времени t1 = 2 с:
на эти оси. Получим для момента времени t1 = 2 с:

После этого находим

Учитывая, что в данном случае угол между  и
и  равен 45°, значение
равен 45°, значение 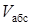 можно еще определить по формуле
можно еще определить по формуле

5. Определение 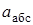 . По теореме о сложении ускорений
. По теореме о сложении ускорений
 (7)
(7)
Для определения 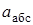 спроектируем обе части равенства (7) на проведенные оси В1xy. Получим
спроектируем обе части равенства (7) на проведенные оси В1xy. Получим

Подставив сюда значения, которые все величины имеют в момент времени t1 = 2 с, найдем, что в этот момент 
Тогда 
Ответ: 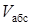 = 3,95 м/с,
= 3,95 м/с, 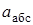 = 12,08 м/с2.
= 12,08 м/с2.
 | Пример К3б. Треугольная пластина ADE вращается вокруг оси z, совпадающей со стороной АЕ, по закону j = f1(t) (положительное направление отсчета угла j показано на рис. К3б дуговой стрелкой). По гипотенузе AD движется точка В по закону s = АВ = f2(t); положительное направление отсчета s – от A к D. Дано: j = 0,1t3 - 2,2t; s = АВ = 2 + 15t – 3t2; (j – в радианах, s – в сантиметрах, t – в секундах). Определить: абсолютную скорость 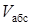 и абсолютное ускорение и абсолютное ускорение 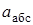 в момент времени t1 = 2 с. в момент времени t1 = 2 с. |
Решение. Рассмотрим абсолютное движение точки В как сложное, считая ее движение по прямойAD относительным, а вращение пластины – переносным (подвижные оси B1xyz связаны с пластиной). Тогда абсолютная скорость  и абсолютное ускорение
и абсолютное ускорение  найдутся по формулам:
найдутся по формулам:
 (1)
(1)
где учтено,что 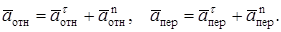
Определим все входящие в равенство (1) величины.
1. Относительное движение (мысленно остановим пластину). Это движение задано естественным способом (см. задачу К1б). Закон движения точки по прямолинейной траектории:
s = AB = 2 + 15t – 3t2, (2)
поэтому 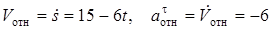 ,
,  , так как для прямой линии
, так как для прямой линии 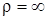 .
.
В момент времени t1 = 2 с имеем
s1 = AB1 = 20 см, Vотн = 3 см/с, аотн = - 6 см/с2. (3)
Знаки показывают, что вектор  направлен в сторону положительного отсчета координаты s, а вектор
направлен в сторону положительного отсчета координаты s, а вектор 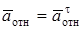 – в противоположную сторону. Изображаем эти векторы на рис. К3б.
– в противоположную сторону. Изображаем эти векторы на рис. К3б.
2. Переносное движение(мысленно остановим движение точки по пластине).Это движение (вращение) происходит по закону j = 0,1t3 - 2,2t.
Найдем угловую скорость w и угловое ускорение e переносного вращения (см. задачу К2): w = 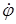 = 0,3t2- 2,2; e =
= 0,3t2- 2,2; e =  = 0,6t и при t1 = 2 с,
= 0,6t и при t1 = 2 с,
w = -1 с-1 , e = 1,2 с-2. (4)
Знаки указывают, что в момент t1= 2 с направление e совпадает с направлением положительного отсчета угла j, а направление w ему противоположно; отметим это на рис. К3б соответствующими дуговыми стрелками.
Из рисунка находим расстояние h1 от точки B1 до оси вращения z:
h1 = АВ1 sin 30° = 10 см. Тогда в момент t1 = 2 с, учитывая равенства (4), получим

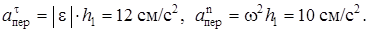 (5)
(5)
Изобразим на рис. К3б векторы  и
и  (с учетом знаков w и e) и
(с учетом знаков w и e) и  ; направлены векторы
; направлены векторы  и
и  перпендикулярно плоскости ADE, а вектор
перпендикулярно плоскости ADE, а вектор  – по линии В1С к оси вращения.
– по линии В1С к оси вращения.
3. Ускорение Кориолиса. Так как угол между вектором  и осью вращения (вектором
и осью вращения (вектором  ) равен 30°, то в момент времени t1 = 2 с
) равен 30°, то в момент времени t1 = 2 с
 (6)
(6)
Направление  найдем по правилу Н.Е. Жуковского. Для этого вектор
найдем по правилу Н.Е. Жуковского. Для этого вектор  спроектируем на плоскость, перпендикулярную оси вращения (проекция направлена противоположно вектору
спроектируем на плоскость, перпендикулярную оси вращения (проекция направлена противоположно вектору  ) и затем эту проекцию повернем на 90° в сторону
) и затем эту проекцию повернем на 90° в сторону  , т. е. по ходу часовой стрелки; получим направление вектора
, т. е. по ходу часовой стрелки; получим направление вектора  . Он направлен перпендикулярно плоскости пластины так же, как вектор
. Он направлен перпендикулярно плоскости пластины так же, как вектор  (см. рис. К3б).
(см. рис. К3б).
4. Определение 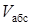 . Так как
. Так как  , а векторы
, а векторы  и
и  взаимно перпендикулярны, то
взаимно перпендикулярны, то  ; в момент времени t1 = 2 с
; в момент времени t1 = 2 с 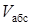 = 10,44 см/с.
= 10,44 см/с.
5. Определениеаабс. По теореме о сложении ускорений
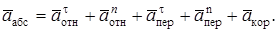 (7)
(7)
Для определения 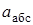 проведем координатные оси В1xyz1ивычислим проекции
проведем координатные оси В1xyz1ивычислим проекции 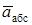 на эти оси. Учтем при этом, что векторы
на эти оси. Учтем при этом, что векторы 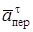 и
и  лежат на оси х, а векторы
лежат на оси х, а векторы  расположены в плоскости В1yz1, т.е. в плоскости пластины. Тогда, проектируя обе части равенства (7) на координатные оси В1хyz1 и учитывая одновременно равенства (3), (5), (6), получим для момента времени t1 = 2с:
расположены в плоскости В1yz1, т.е. в плоскости пластины. Тогда, проектируя обе части равенства (7) на координатные оси В1хyz1 и учитывая одновременно равенства (3), (5), (6), получим для момента времени t1 = 2с:

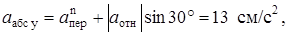

Отсюда находим значение 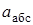 :
: 
Ответ: Vабс = 10,44 см/с, аабс = 16,64 см/с2.
