Обыкновенные дифференциальные

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ

УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Общие понятия

Определение. Обыкновенным дифференциальным уравнением (ОДУ) первого порядка называется уравнение вида

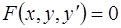, (1.1)

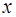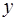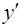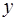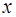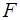где - независимая переменная; - искомая функция этой переменной; - производная от по ; - заданная функция своих аргументов.

Определение. Непрерывно дифференцируемая на некотором интервале 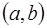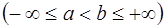функция 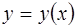, которая при подстановке в уравнение (1.1) обращает его в тождество по 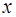на , на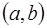зывается решением этого уравнения.

График решения 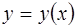ОДУ (1.1) есть его интегральная кривая.

Если уравнение (1.1) удается записать в виде

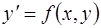, (1.2)

то последнее называют ОДУ, разрешенным относительно производной. В настоящем учебном пособии рассматриваются именно такие уравнения.

Часть 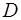плоскости 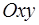, в которой функция 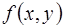непрерывна, называется областью задания ОДУ (1.2).

Определение. Задачей Коши для уравнения (1.2) называется задача отыскания решения 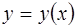этого уравнения, удовлетворяющего условию

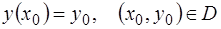. (1.3)

Условие (1.3) – начальное условие, а числа 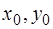- начальные данные задачи Коши (1.2) – (1.3).

Геометрическая интерпретация задачи Коши – найти интегральную кривую ОДУ (1.2), проходящую через точку .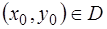

Говорят, что решение задачи Коши для уравнения (1.2) с начальным условием (1.3) единственно, если существует такая окрестность точки 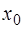, что

1) в этой окрестности определено решение с начальными данными ;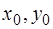

2) не существует другого решения с начальными данными 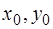, определенного в той же окрестности.

Имеет место следующая теорема существования и единственности решения задачи Коши (1.2) – (1.3).

Теорема. Если в области 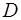плоскости 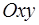функция 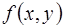и ее частная производная 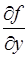непрерывны по совокупности аргументов, то существует единственное решение 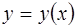уравнения (1.2), удовлетворяющее начальному условию

.

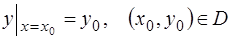Пусть 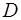есть область в плоскости 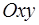, через каждую точку которой проходит одна и только одна интегральная кривая ОДУ (1.2). В дальнейшем такую область условимся называть областью существования и единственности решения задачи Коши или, более кратко, областью существования и единственности рассматриваемого уравнения.

Определение.Функция

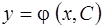, (1.4)

определенная в некоторой области изменения переменных 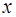и 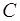и непрерывно дифференцируемая по 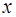, называется общим решением уравнения (1.2) в области 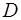, если

1) равенство (1.4) разрешимо в 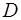относительно :

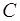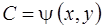, (1.5)

2) функция (1.4) является решением ОДУ (1.2) при всех значениях 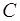, определяемых формулой (1.5), когда точка 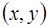пробегает

область .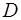

Переменная 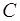в (1.4) называется произвольной постоянной (константой).

Определение.Равенство 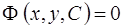, неявно задающее общее решение, называется общим интегралом ОДУ (1.2).

Решение 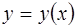уравнения (1.2) называется частным, если в каждой точке соответствующей ему интегральной кривой сохраняется единственность решения задачи Коши. Через каждую точку 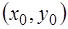такой кривой проходит единственная интегральная кривая уравнения (1.2).

Определение. Решение 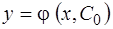, получающееся из общего решения (1.4) фиксированием произвольной константы 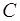, есть частное решение.

Определение. Говорят, что решение 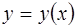уравнения (1.2) особое, если в каждой точке соответствующей ему интегральной кривой нарушается единственность решения задачи Коши.

Если функция 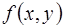, в правой части ОДУ (1.2) непрерывна по 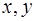и имеет частную производную по 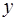(ограниченную или нет), то особыми решениями могут быть только те кривые, во всех точках которых

.

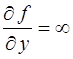Если в некоторых точках плоскости 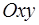функция 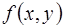обращается в бесконечность, то в окрестности таких точек рассматривают перевернутое по отношению к (1.2) уравнение

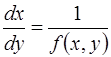, (1.6)

в котором считают 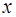функцией от 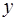. Совокупность таких точек присоединяют к области задания уравнения (1.2), а решения 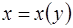уравнения (1.6) – к решениям ОДУ (1.2).

Уравнениям (1.2) и (1.6) равносильно ОДУ первого порядка в дифференциальной форме вида

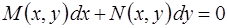. (1.7)

Оно не задано в тех точках 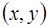, где непрерывные функци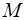и и 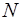обращаются в нуль одновременно. В уравнение (1.7) переменные 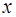и 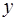входят равноправно. При решении конкретных уравнений вида (1.7) часто бывает удобно в отличие от традиционных обозначений рассматривать переменную величину 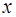как функцию от .

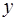Ниже в пунктах 1.2 – 1.6 рассматриваются различные типы дифференциальных уравнений первого порядка, разрешенных относительно производной, и методы их решения.

Переменными

Определение. Уравнение с разделенными переменными – это уравнение вида

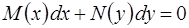или 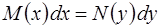, (1.8)

где 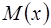и 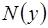функции, зависящие только от х и y соответственно, являющиеся непрерывными при рассматриваемых значения х и y.

Общим интегралом такого уравнения является равенство

,

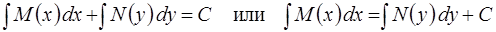в котором под выражениями 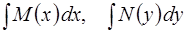понимаются произвольные первообразные функций М и N, соответственно, С – произвольная постоянная.

Пример 1. Проверить, что общим интегралом ОДУ 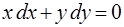в области 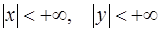, является равенство

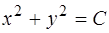. (1.9)

Решение.Действительно, проинтегрировав его левую часть, получим

,

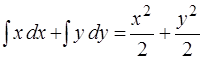следовательно, общим интегралом рассматриваемого уравнения является соотношение

,

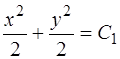откуда, в силу произвольности константы 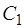, следует (1.9), где .

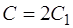Пример 2. Уравнение

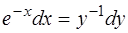
при 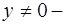интегрируется так:

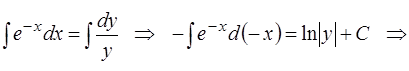
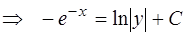или ,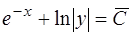

где 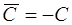, следовательно, общий интеграл имеет вид

,

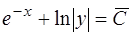где 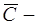произвольная константа.

Определение. Уравнение вида

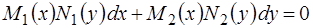, (1.10)

в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от х и только от y, называется уравнением с разделяющимися переменными.

Умножением обеих частей этого уравнения на функцию

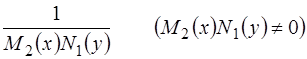, (1.11)

оно приводится к уравнению (1.8) с разделенными переменными. Поэтому общий интеграл ОДУ (1.10) есть

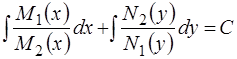. (1.12)

Если уравнения 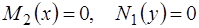имеют действительные решения x=a и y=b, то функции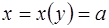 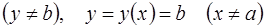, являясь решением (1.10), могут не входить в общий интеграл (1.12) ни при каком конечном значении С, хотя при этом среди них могут быть частные решения (1.10), то есть последние при интегрировании оказываются потерянными. Точки вида х=а, y=b исключаются из интегральных кривых, соответствующих решениям 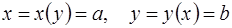, так как в этих точках уравнение (1.10) не задано. Необходимо отметить также, что среди решений 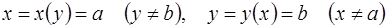могут быть и особые решения ОДУ (1.10).

Пример 3. Проинтегрировать уравнение

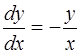. (1.13)

Решение. Обе части уравнения умножим на функцию 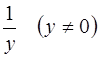, тогда его можно записать в дифференциальной форме

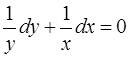. (1.14)

Получили уравнение с разделенными переменными. Его общий интеграл при при 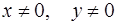есть соотношение

,

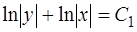где 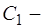произвольная постоянная. Константу 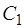представим в виде 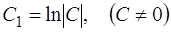, тогда 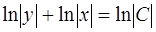, откуда имеем 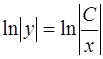или 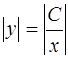. В последнем соотношении, в силу произвольности 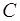, знаки модуля можно опустить. Следовательно,

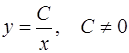. (1.15)

Очевидно, решение 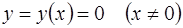уравнения (1.13) не входит в последнюю формулу ни при каком значении 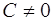, хотя соответствующая ему интегральная кривая лежит в областях существования и единственности решения задачи Коши этого уравнения, то есть решение 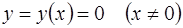оказалось потерянным. Однако оно входит в формулу (1.15) при 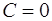. Поэтому, допуская в (1.15) и 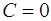, получаем, что общее решение уравнения (1.13) при 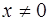имеет вид

,

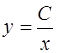где 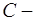произвольная постоянная.

Заметим, что функция 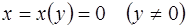является решением перевернутого по отношению к (1.13) уравнения

.

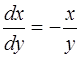Пример 4. Найти решение дифференциального уравнения

,

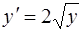удовлетворяющее начальному условию .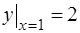

Решение. Разделим переменные, умножив обе части уравнения на 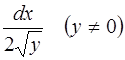. Имеем

.

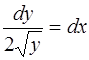Интегрируя последнее уравнение, получаем

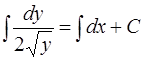
или

.

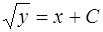Так как 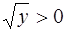, то в последнем соотношении 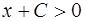. Отсюда находим общее решение данного уравнения в области :

.

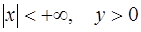Выделим частное решение, удовлетворяющее начальному условию 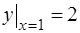. Для этого в формуле общего решения положим 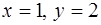, получим уравнение для определения значения константы 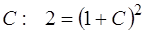. Из него находим 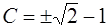. Из двух, значени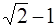й и 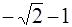выбираем 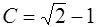, так как точка 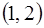не лежит на кривой .

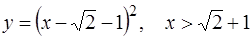Итак, искомое решение есть .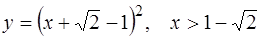

Пример 5. Найти общий интеграл уравнения

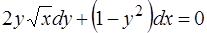. (1.16)

Решение. ОДУ (1.16) – это уравнение с разделяющимися переменными. Умножив обе части его на функцию

,

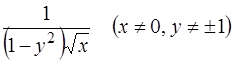получим уравнение с разделенными переменными

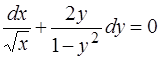. (1.17)

Общим интегралом последнего является соотношение

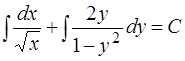
или

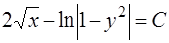. (1.18)

Следовательно, (1.18) есть общий интеграл ОДУ (1.16).

Заметим, что формула (1.18) получена в предположении, что 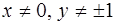. Функци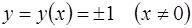и и 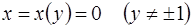являются, очевидно, решениями (1.16) и они не входят в (1.18) ни при каком конечном значении константы С. Покажем, что функции 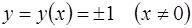являются частными, а функция 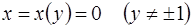– особым решением уравнения (1.16).

Действительно, полупрямые 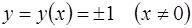лежат в областях существования и единственности уравнения

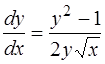, (1.19)

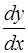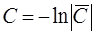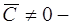получающегося из (1.16) разрешением относительно . Значит, эти полупрямые есть частные решения ОДУ (1.19), а следовательно и (1.16). Записав общий интеграл (1.18) в иной форме, выделим из него эти частные решения. Положим в (1.18) , где произвольная константа, тогда (1.18) перепишется так:

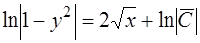
или

.

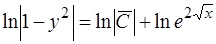Отсюда имеем 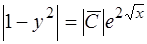и, в силу произвольности ,

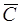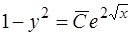. (1.20)

Соотношение (1.20) - также общий интеграл ОДУ (1.16). Оно получено в предположении 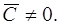Очевидно, решения 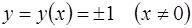уравнения (1.16) получаются из (1.20) при значении 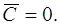Но, как мы показали, эти решения – частные, следовательно, в (1.20) можно допускать и 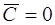. Таким образом, частные решения 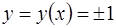уравнения (1.16) получаются из общего интеграла (1.20) этого уравнения при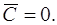

Покажем сейчас, что функция 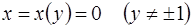является особым решением уравнения (1.16). Отметим, во-первых, что соответствующая ей интегральная кривая не лежит в областях существования и единственности уравнения

,

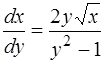перевернутого по отношению к (1.19), так как частная производная по 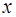функции 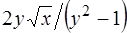в точках прямой 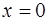обращается в бесконечность. Убедимся теперь в том, что через каждую точку интегральной кривой 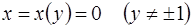проходит по крайней мере две интегральные кривые уравнения (1.16). Выберем произвольно точку 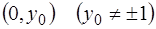на этой кривой и ее координаты подставим в общий интеграл (1.20). Будем иметь соотношение для определения :

.

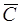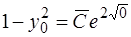Отсюда находится кривая 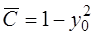. Таким образом, интегральная кривая 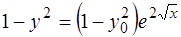также проходит через точку 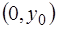, то есть функция 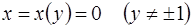– особое решение ОДУ (1.16).

1.2.1.Примеры для самостоятельного решения

Проинтегрировать следующие дифференциальные уравнения.

1. ,

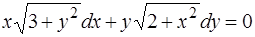2. ,

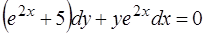3. ,

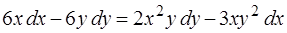4. ,

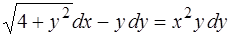5. ,

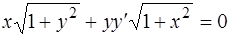6. .

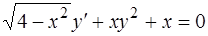Решить задачу Коши.

1. ,

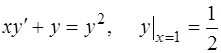2. .

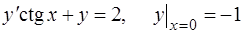Уравнения Бернулли

Определение. Уравнение вида

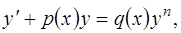(1.38)

где 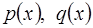– непрерывные на некотором интервале 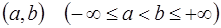функции, 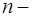действительное число, отличное от 0 и 1, называется уравнением Бернулли.

Делением обеих частей на 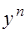и подстановкой 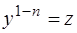, где 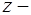новая неизвестная функция, это уравнение приводится к линейному уравнению

.

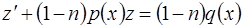Заметим, что при делении обеих частей уравнения (1.38) на 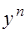при 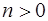возможна потеря решения 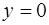. Это решение является частным, если 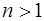, и особым, если .

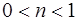Пример 1. Решить уравнение

.

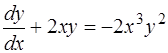Решение. Обе части уравнения разделим на 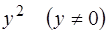, тогда будем иметь:

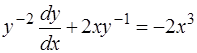. (1.39)

Положим 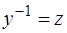, откуда 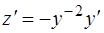. В силу введенной подстановки уравнение (1.39) можно записать следующим образом:

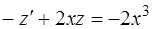
или

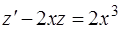(1.40)

Последнее уравнение – линейное относительно функции 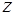. Его общее решение есть

,

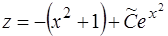где 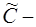произвольная константа (см. п.1.4., пример 1). Отсюда, учитывая, что 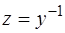, записываем общий интеграл исходного уравнения

.

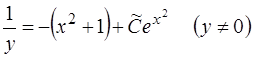Так как показатель степени 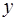в правой части нашего уравнения равен 2, то потерянное при интегрировании решение 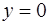является частным.

Замечание.При интегрировании уравнения Бернулли можно также непосредственно применить подстановку 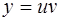или метод вариации произвольной постоянной.

Пример 2. Проинтегрировать уравнение

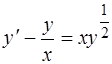. (1.41)

Решение. Уравнение (1.41) – это уравнение Бернулли. Положим 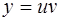, тогда (1.41) запишется в виде

.

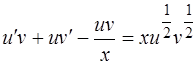или

.

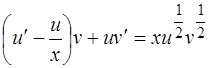Функцию 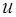выберем так, чтобы 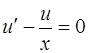. Например, пусть 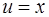. Подставив 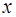вместо 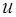в последнее уравнение и учитывая, что 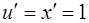, для определения 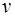будем иметь уравнение

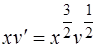. (1.42)

Последнее уравнение – это уравнение с разделяющимися переменными, его общий интеграл есть

,

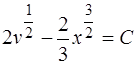откуда

,

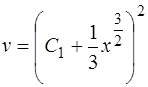где 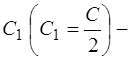произвольная константа. Следовательно, общее решение ОДУ (1.41) есть

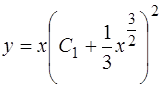. (1.43)

Заметим, что при интегрировании уравнения (1.42) методом разделения переменных мы теряем решение 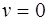, это ведет к потере решения 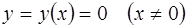уравнения (1.41). Так как в правой части (1.41) стоит степень 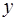с показателем 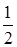, то теряемое решение является особым.

Рассмотрим другой способ решения уравнения (1.41), а именно проинтегрируем его методом вариации произвольной постоянной. Запишем однородное уравнение, соответствующее (1.41):

.

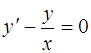Его общее решение есть 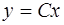. Пусть С= С(х), тогда общее решение (1.41) будем искать в виде

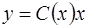. (1.44)

Подставив 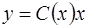и 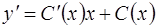в уравнение, будем иметь

,

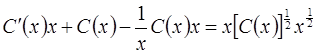или

.

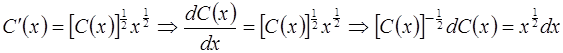Проинтегрировав последнее уравнение, находим

,

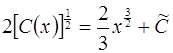или

,

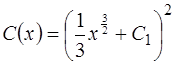где 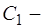произвольная константа, 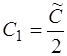. Подставляя С(х) в (1.44), получаем общее решение уравнения (1.44) в форме (1.43)

.

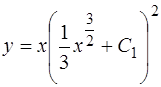1.5.1. Примеры для самостоятельного решения

Решить уравнения.

1. 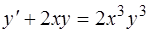, 3. .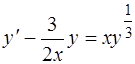

2. ,

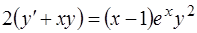Найти решение задач Коши.

1. 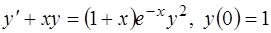; 3. .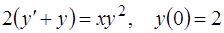

2. ;

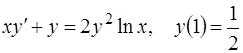ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ

УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Общие понятия

Определение. Обыкновенным дифференциальным уравнением (ОДУ) первого порядка называется уравнение вида

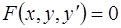, (1.1)

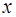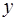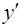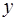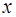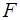где - независимая переменная; - искомая функция этой переменной; - производная от по ; - заданная функция своих аргументов.

Определение. Непрерывно дифференцируемая на некотором интервале 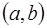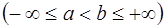функция 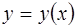, которая при подстановке в уравнение (1.1) обращает его в тождество по 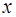на , на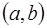зывается решением этого уравнения.

График решения 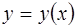ОДУ (1.1) есть его интегральная кривая.

Если уравнение (1.1) удается записать в виде

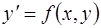, (1.2)

то последнее называют ОДУ, разрешенным относительно производной. В настоящем учебном пособии рассматриваются именно такие уравнения.

Часть 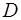плоскости 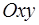, в которой функция 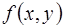непрерывна, называется областью задания ОДУ (1.2).

Определение. Задачей Коши для уравнения (1.2) называется задача отыскания решения 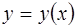этого уравнения, удовлетворяющего условию

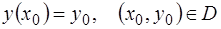. (1.3)

Условие (1.3) – начальное условие, а числа 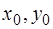- начальные данные задачи Коши (1.2) – (1.3).

Геометрическая интерпретация задачи Коши – найти интегральную кривую ОДУ (1.2), проходящую через точку .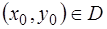

Говорят, что решение задачи Коши для уравнения (1.2) с начальным условием (1.3) единственно, если существует такая окрестность точки 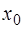, что

1) в этой окрестности определено решение с начальными данными ;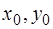

2) не существует другого решения с начальными данными 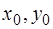, определенного в той же окрестности.

Имеет место следующая теорема существования и единственности решения задачи Коши (1.2) – (1.3).

Теорема. Если в области 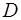плоскости 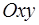функция 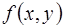и ее частная производная 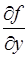непрерывны по совокупности аргументов, то существует единственное решение 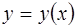уравнения (1.2), удовлетворяющее начальному условию

.

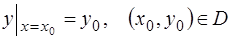Пусть 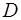есть область в плоскости 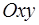, через каждую точку которой проходит одна и только одна интегральная кривая ОДУ (1.2). В дальнейшем такую область условимся называть областью существования и единственности решения задачи Коши или, более кратко, областью существования и единственности рассматриваемого уравнения.

Определение.Функция

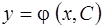, (1.4)

определенная в некоторой области изменения переменных 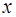и 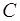и непрерывно дифференцируемая по 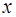, называется общим решением уравнения (1.2) в области 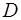, если

1) равенство (1.4) разрешимо в 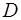относительно :

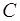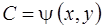, (1.5)

2) функция (1.4) является решением ОДУ (1.2) при всех значениях 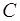, определяемых формулой (1.5), когда точка 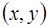пробегает

область .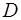

Переменная 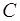в (1.4) называется произвольной постоянной (константой).

Определение.Равенство 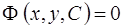, неявно задающее общее решение, называется общим интегралом ОДУ (1.2).

Решение 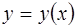уравнения (1.2) называется частным, если в каждой точке соответствующей ему интегральной кривой сохраняется единственность решения задачи Коши. Через каждую точку 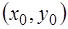такой кривой проходит единственная интегральная кривая уравнения (1.2).

Определение. Решение 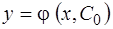, получающееся из общего решения (1.4) фиксированием произвольной константы 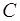, есть частное решение.

Определение. Говорят, что решение 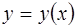уравнения (1.2) особое, если в каждой точке соответствующей ему интегральной кривой нарушается единственность решения задачи Коши.

Если функция 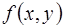, в правой части ОДУ (1.2) непрерывна по 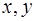и имеет частную производную по 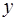(ограниченную или нет), то особыми решениями могут быть только те кривые, во всех точках которых

.

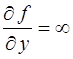Если в некоторых точках плоскости 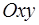функция 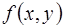обращается в бесконечность, то в окрестности таких точек рассматривают перевернутое по отношению к (1.2) уравнение

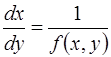, (1.6)

в котором считают 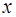функцией от 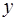. Совокупность таких точек присоединяют к области задания уравнения (1.2), а решения 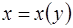уравнения (1.6) – к решениям ОДУ (1.2).

Уравнениям (1.2) и (1.6) равносильно ОДУ первого порядка в дифференциальной форме вида

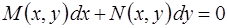. (1.7)

Оно не задано в тех точках 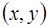, где непрерывные функци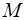и и 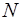обращаются в нуль одновременно. В уравнение (1.7) переменные 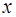и 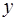входят равноправно. При решении конкретных уравнений вида (1.7) часто бывает удобно в отличие от традиционных обозначений рассматривать переменную величину 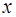как функцию от .

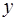Ниже в пунктах 1.2 – 1.6 рассматриваются различные типы дифференциальных уравнений первого порядка, разрешенных относительно производной, и методы их решения.