Механические методы выравнивания динамического ряда

Если динамический ряд составлен из уровней за короткие промежутки времени, то под влиянием множества факторов, которые действуют на уровни в разных направлениях, наблюдается колеблемость данных уровней в сторону повышения или снижения, из-за чего основная тенденция развития не просматривается.

Наиболее простым способом выявления основной тенденции развития является – метод укрупнения интервалов. Данный метод заключается в том, что первоначально полученный динамический ряд преобразуется в другой, уровни которого относятся к более продолжительным периодам времени. Например, ряд состоящий из уровней за месячный период, заменяется рядом с квартальными уровнями, ряд годовых уровней заменяется на пятилетия, и т.д. Новый динамический ряд образуется либо суммированием абсолютных величин первоначальных уровней, либо путем расчета средних уровней в объединенном периоде времени. При этом отклонения в уровнях укрупненного динамического ряда сглаживаются (взаимопогашаются) и более четко проявляется основная тенденция развития явления.

Другим методом механического выравнивания динамического ряда является метод скользящей средней. Данный метод заключается в замене исходного динамического ряда новым, расчетным рядом состоящим из средних уровней, за определенный период, со сдвигом на одну дату. Если исходный динамический ряд обозначить как: , то выроненный методом скользящей средней будет выглядеть как:

1. за трехлетний период

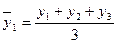
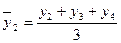
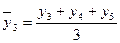
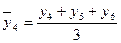и т.д. (6.24)

2. за пятилетний период

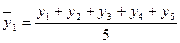
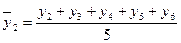
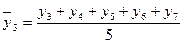
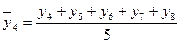и т.д. (6.25)

Выбор временного периода сглаживания, как правило, выбирается производно, в основном зависит от числа уровней в исходном динамическом ряду, так как новый динамический ряд сократится на 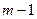уровней, где 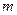– число членов скользящей средней. Например, если сглаживание проводится за 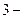летний период, то выровненный динамический ряд сократится на 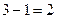уровней, если за 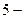летний период то на 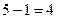уровня.

Также, некоторую сложность, вызывает исследование динамического ряда, методом средних скользящих, состоящего из четного количества уровней. Если число членов средней скользящей обозначить как 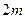, то серединным будет уровень 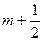члена ряда, т.е. наблюдается сдвиг периода, к которому относится серединный уровень. Так, например, при расчете скользящей средней для четырех уровней средняя для первого четырехлетия находится между вторым и третьем уровнями, для следующего четырехлетия между третьим и четвертым уровнями и т.д. Для того чтобы избежать данных сдвигов существует несколько методов. Наиболее часто применяемым, в силу своей простоты, является метод преобразования. При данном методе первый уровень первого интервала входит в сумму расчета средней только наполовину, затем берутся все остальные уровни первого интервала и половина первого уровня из следующего интервала. Например, для четырех летнего периода:

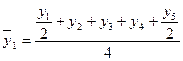
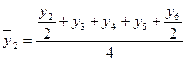
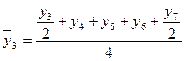и т.д. (6.26)

Методы механического выравнивания рядов динамики являются только первоначальными, предварительными, эмпирическими методами, которые подготавливают исходные данные для более сложных методов выражающих общую тенденцию развития.

1.6.2.3 Аналитическое выравнивание динамического ряда

Аналитическое выравнивание позволяет определить основную тенденцию развития явления во времени. При этом уровни ряда динамики выражаются как функции времени:

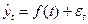, (6.27)

где 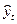- уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени ,

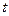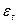- отклонение от тенденции (случайное и циклическое)

В итоге выравнивания динамического ряда получают обобщенный (суммарный), проявляющийся во времени результат действия всех факторов влияющих на развития изучаемого явления во времени.

При проведение аналитического выравнивания определяется зависимость 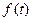, при этом выбирается такая функция 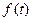, чтобы она показывала содержательное объяснение изучаемого процесса. При аналитическом выравнивании, чаще всего применяют следующие трендовые модели:

1. линейная 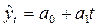(6.28)

2. парабола второго порядка 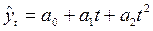(6.29)

3. кубическая парабола 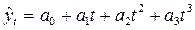(6.30)

4. показательная 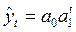(6.31)

5. экспоненциальная 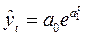(6.32)

6. модифицированная экспонента 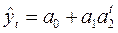(6.33)

7. кривая Гомперца 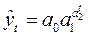(6.34)

8. логистическая кривая 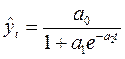(6.35)

9. логарифмическая парабола 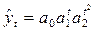(6.36)

10. гиперболическая 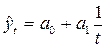(6.37)

Чаще всего выбор функции кривой проводится при помощи анализа графического изображения динамического ряда. Но по графику исходных уровней не всегда можно точно определить форму зависимости. Поэтому часто используют не исходный динамический ряд, а ряд механически сглаженных уровней, в котором случайные колебания гасятся в той или иной мере.

Кроме анализа графического изображения, для выбора формы кривой рассматривают ряд признаков:

1. если в исходном динамическом ряду наблюдаются более или менее постоянные разности первого порядка (абсолютные приросты), то есть не наблюдается тенденция к их увеличению или уменьшению выбирается линейная зависимость.

2. первые разности сами по себе имеют некоторую тенденцию развития, но вторые разности (абсолютные приросты абсолютных приростов) имеют примерно одну и ту же величину - применяют параболу второго порядка

3. если рост уровней исходного ряда идет по геометрической прогрессии, применяется показательная функция.

4. если первые разности имеют тенденцию к уменьшению с постоянным темпом – модифицированная экспонента.

5. если средние уровни, нанесенные на полулогарифмическую сетку, близки к прямой линии - простая экспонента.

6. если первые разности обратных значений средних уровней изменяются на один и тот же процент – логистическая кривая.

Оценку параметров уравнений 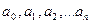осуществляют при помощи:

1. метода наименьших квадратов (МНК)

2. метода наименьших расстояний

3. метода избранных точек.

Чаще всего используют метод наименьших квадратов, который обеспечивает наименьшую сумму квадратов отклонений фактических уровней динамического ряда от уровней выровненного динамического ряда.