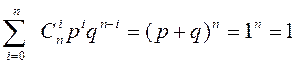Раздел 20.2. Случайные величины с дискретным распределением

Как мы уже говорили, событие, связанное со случайной величиной, заключается в том, что эта функция принимает какое-то значение и вероятность этого значения мы можем обсуждать.

Определение. Случайная величина, которая может принимать лишь конечное или счётное число значений, называется дискретной.

Если говорится, что задана случайная величина Х, это значит, что каждому исходу w_k случайного эксперимента поставлено в соответствие единственное число x_k, что записывается в виде равенства x_k = Х(w_k).

Некоторые из значений x_k могут совпадать, то есть различным исходам w может соответствовать одно и то же число x. Если все значения случайной величины совпадают, то будем говорить, что случайная величина постоянна.

Пусть А_k — множество всех элементарных исходов, каждому из которых соответствует значение x_k (k = 1,2,¼,n) случайной величины Х. То есть А_k как множество, состоит из всех тех w_k , для которых Х(w_k)= x_k .

Таким образом, А_k – это событие (строго говоря, это верно лишь в случае конечного или счётного числа исходов). Для каждого события А_k определим число р_k ³ 0, равное вероятности этого события: р_k = P(A_k). Очевидно, что

Объединение всех А_k совпадает с W, A_i∩A_j = Æ (i,j = 1,2,¼,n, i¹j), .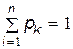

Теперь каждому значению x_k случайной величины Х можно поставить в соответствие вероятность р_k = P(A_k) события А_k. Если такое соответствие определено, то будем говорить, что задан закон распределения диск­ретной случайной величины Х. Обычно закон распределения диск­ретной случайной величины представляется в виде таблицы

Х	х1	х2	х3	¼	хn
P	p1	p2	p3	¼	pn

В дальнейшем для краткости будем называть величину p_i вероятностью значения х_i случайной величины, т.е. р_k = P(Х=х_k). Отметим, что закон распределения содержит всю информацию о случайной величине, и задать случайную величину можно, просто представив её закон распределения.

Итак, закон распределения дискретной случайной величины – это таблица, состоящая из двух строк – значений случайной величины и соответствующих вероятностей, причем необходимым условием является .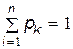

Замечание. Может возникнуть вопрос: а как же быть с равенством 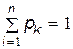в случае, если значений случайной величины не конечное, а бесконечное (но счетное) количество? В таком случае сумму нужно понимать как сумму соответствующего числового ряда.

Замечание. Иногда, особенно в случае счетного числа значений случайной величины, в качестве закона распределения дискретной случайной величины рассматривают формулу для вероятности принятия конкретного значения (как, скажем, для биномиального или пуассоновского распределения). Нетрудно видеть, что с помощью такой формулы легко получить искомую таблицу. Возможно, правда, бесконечную…

Замечание. Можно представить себе модель дискретного распределения более наглядно следующим образом: рассмотрим «физический» стержень – координатную прямую, несгибаемый стержень, на котором мы разместим «грузы». В физике пользуются понятием «точечная масса»- масса, сосредоточенная в точке, не имеющая объема. Поместим такие массы в точках с координатами, соответствующими значениям случайной величины. Эти массы по величине будут совпадать с величиной вероятности соответствующего значения. Тем самым мы получим дискретное распределение массы-вероятности, она будет сосредоточена лишь в некоторых точках, с промежутками. Именно этой модели теория вероятностей обязана употребляющемуся в некоторых изданиях выражению «значения случайной величины с весом».

Теперь построим функцию распределения дискретной случайной величины.

Напомним, что функция распределения случайной величины Х – это вероятность F_X (x) = Р(X<x)

Пусть у нас есть таблица закона распределения, значения случайной величины в ней расположены по возрастанию, т.е. х₁ ≤ х₂≤…≤ х_n . Тогда для любых х ≤ х₁ событие, состоящее в том, что случайная величина приняла значение меньшее х, т.е. {Х<х}, есть событие невозможное, вероятность которого равна 0. Если х₁ <x ≤ х₂ , то событие {Х<х} состоит только из тех элементарных исходов ω, для которых Х( ω ) = х₁ и соответственно F_X (x) =р₁.

Аналогично, когда х₂ <x ≤ х₃ событие {Х<х} состоит только из тех элементарных исходов ω, для которых Х( ω ) = х₁ илиХ( ω ) = х₂ и соответственно, то есть событие {Х<х} состоит из двух (несовместных) событий {Х=х₁} и {Х<х₂} , {Х<х} = {Х=х₁} + {Х<х₂} F_X (x) =р₁+ р_2.

И так далее. Когда же, наконец, значение переменной х превзойдет максимальное значение случайной величины х_n, т.е. x > х_n, событие {Х<х} = {Х=х₁} + {Х<х₂}+…{Х<х_n} окажется достоверным событием и F_X (x) = р₁+ р₂+…+ р_n=1. Таким образом, функция распределения оказывается кусочно-постоянной, непрерывной слева.

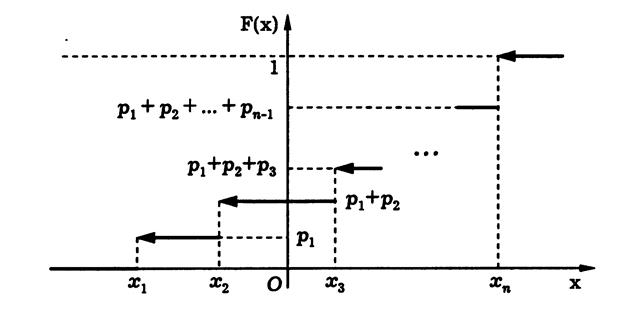
Замечание. На графике знак ← соответствует промежутку (…], то есть, левый конец промежутка исключен, а правый – включен. (Этому же соот-ветствует также употребляющийся в этом случае графический знак ○── )

Примеры дискретных распределений

Равномерное распределение

Дискретная величина принимает конечное число значений с одинаковыми вероятностями. Например, случайная величина принимает значение числа на верхней грани кубика при однократном подбрасывании

Х	х1	х2	х3	¼	хn
P				¼

Биномиальное распределение

Случайная величина принимает значение числа успехов в схеме Бернулли из n испытаний .p – вероятность успеха q – вероятность неудачи в одном испытании, 0<p,q<1, p+q=1

P{X =i} =

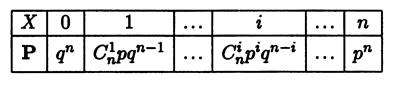
Сумма в нижней строке есть биномиальное разложение для (p+q)ⁿ =