Повторные независимые испытания. Схема Бернулли. Формула Бернулли.

Приведем вначале небольшую выдержку из классического учебника В.Феллера «Введение в теорию вероятностей и ее приложения», т.1, глава VI, §1 «Испытания Бернулли»

Рассмотрим случай многократного повторения одного и того же испытания или случайного эксперимента. Результат каждого испытания будем считать не зависящим от того, какой результат наступил в предыдущих испытаниях. В качестве результатов или элементарных исходов каждого отдельного испытания будем различать лишь две возможности:

1) появление некоторого события А (успех);

2) появление события , (события, являющегося дополнением А, неудача))

Пусть вероятность P(A) появления события А постоянна и равна p (0<p<1). Вероятность P( ) события обозначим через q: P( ) = 1- p=q.

Примерами таких испытаний могут быть:

1) подбрасывание монеты: А - выпадение герба; - выпадение решетки

P(A) = P( ) = 0,5.

2) бросание игральной кости: А - выпадение количества очков, равного пяти, выпадение любого количества очков кроме пяти.

P(A) =1/6, P( ) =5/6.

3) извлечение наудачу из урны, содержащей 7 белых и 3 черных шара, одного шара (с возвращением): А - извлечение белого шара, - извлечение черного шара

P(A) = 0,7; P( ) = 0,3

Замечание 19.1.1. Термины «Успех» и «неудача» несколько отличаются по смыслу от «бытового» смысла этих понятий. «Успех» означает лишь, что нечто произошло, но в общеупотребительном смысле это может быть совсем не радостным событием (скажем, авария, выявление тяжелого заболевания, травмы и т.д.)

Замечание 19.1.2.. Традиционно успех, помимо буквы «У», обозначают 1,а неудачу – 0. Поэтому последовательности из успехов и неудач – реализацию испытаний конкретной схемы Бернулли – можно уподобить последовательность из нулей и единиц.

Таким образом, элементарным событием (исходом) в схеме Бернулли из n испытаний будет последовательность из n нулей или единиц (успехов или неудач). Например, при трехкратном подбрасывании кубика, когда успехом является, например, выпадение 6, (а неудачей, соответственно, выпадение любого числа от 1 до 5, но не 6), элементарными исходами будут тройки из нулей и единиц от (1,1,1) до (0,0,0).

Пусть произведено n испытаний, которые мы будем рассматривать как один сложный случайный эксперимент. Составим таблицу из n клеток, расположенных в ряд, пронумеруем клетки, и результат каждого испытания будем отмечать так: если в i-м испытании событие А произошло, то в i-ю клетку ставим цифру 1, если событие А не произошло (произошло событие ), в i-ю клетку ставим 0.

Если, например, проведено 5 испытаний, и событие А произошло лишь во 2 -м и 5-м испытаниях, то результат можно записать такой последовательностью нулей и единиц: 0; 1; 0; 0; 1.

Каждому возможному результату n испытаний будет соответствовать последовательность n цифр 1 или 0, чередующихся в том порядке, в котором появляются события A и в n испытаниях, например:

1; 1; 0; 1; 0; 1; 0; 0; ... 0; 1; 1; 0

Всего таких последовательностей можно составить 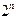(согласно правилу произведения и определению независимых событий).

Так как испытания независимы, то вероятность P каждого такого результата определяется путем перемножения вероятностей событий A и в соответствующих испытаниях. Так, например, для написанного выше результата найдем

P = p×p×q×p×q×p×q×q×...×q×p×p×q

Если в написанной нами последовательности единица встречается х раз (это значит, что нуль встречается n-x раз), то вероятность соответствующего результата будет pⁿq^n-x независимо от того, в каком порядке чередуются эти x единиц и n-x нулей.

Замечаниие 19.3.. Рассмотрим случай, когда некто подкидывает монетку и, в зависимости от результата, записывает 1 (выпал Герб) или 0 (выпала решетка). Через некоторое время у него появляется вереница из 0 и 1. Возникает вопрос, а в каком случае данная последовательность будет случайной? Будет ли таковой, скажем, последовательность 01010101010101010101 , 01001000100010000010 или 10000000000000000000? Ответ на этот вопрос, к сожалению, выходит за рамки данного курса, но интригующе интересен и имеет непосредственное отношение к теории алгоритмов и теории сложности. Для начала можно адресовать заинтересовавшихся к лекции В.А.Успенского «Четыре алгоритмических лица случайности» (Изд. МЦНМО, 2006). Приведем лишь короткую цитату из нее:

«Составленная из нулей и единиц цепочка 100010111011110100000111 выглядит более случайной, чем цепочка 010101010101010101010101. Возможно ли разделить все цепочки нулей и единиц на случайный и не случайные? Для конечных цепочек эта задача вряд ли осуществима. Однако можно пытаться решать её для бесконечных цепочек, т.е. для последовательностей. Иными словами, можно пытаться найти строгое математическое определение для понятия "случайная последовательностей нулей и единиц".
Традиционная теория вероятностей не только не приближается к решению этой задачи, но даже не может её сформулировать в своих терминах. На помощь приходит теория алгоритмов. Может показаться парадоксальным, что понятие случайности уточняется на основе такого чуждого случайности понятия, как алгоритм, - тем не менее, это так: все известные до сих пор определения случайности индивидуального объекта (в нашем примере - индивидуальной последовательности нулей и единиц) опираются на понятие алгоритма.
Чтобы найти требуемое определение, поступают так. Формулируют некое характеристическое свойство, которым обладают случайные (в неформальном, интуитивном смысле) последовательности. А затем последовательности, обладающие этим свойством, и объявляют, по определению, случайными. Какими же свойствами обладает случайная последовательность нулей и единиц?

1. Во-первых, она частотноустойчива. Вот что это означает для того простейшего случая, когда нули и единицы равновероятны - а только такой случай мы и будем рассматривать: частота нулей, как и частота единиц, стремится к одной второй. При этом указанная устойчивость частот выполняется не только для последовательности в целом, но и для любой её законной, разумной подпоследовательности.

2. Во-вторых, она хаотична. Это означает, что чередование нулей и единиц не может быть описано никаким разумным правилом.

3. В-третьих, она типична. Это означает, что она принадлежит любому разумному большинству.

4. В-четвёртых, она непредсказуема. Это означает, что играя против неё на деньги (то есть пытаясь угадать члены последовательности и делая ставки), последовательность невозможно обыграть, какой бы разумной стратегией не пользоваться.

Слово "разумный", встречающееся в описаниях перечисленных четырёх свойств, разумеется, нуждается в уточнении. Теория алгоритмов как раз и предлагает такие уточнения, наполняя это слово точным смыслом - своим для каждого из наших четырёх свойств. Тем самым возникают четыре алгоритмических свойства: частотная устойчивость, хаотичность, типичность, непредсказуемость. Каждое из них представляет своё собственное алгоритмическое лицо случайности, и каждое из них с большими или меньшими основаниями может претендовать на роль строгого математического определения для понятия случайности. Можно сказать и так: возникают четыре точно очерченных класса последовательностей, каждый из которых претендует на то, чтобы служить истинным классом случайных последовательностей; некоторые из этих претензий более оправданы, чем другие».

Замечание 19.1.4. Пусть у нас есть схема испытаний Бернулли, в каждом из которых происходит (Успех, У) или не происходит (Неудача, Н) некоторое событие А. Вероятность и того и другого постоянна и не зависит от номера испытания. Мы может теперь интересоваться различными вопросами, связанными не только с распределением успехов и неудач внутри серии, но и с их количеством.

Таковы например вопросы:

- о вероятности ровно m успехов в серии из n испытаний,

- о вероятности принадлежности числа успехов m промежутку от m₁ до m₂ ,

- о вероятности ровно m неудач до первого успеха и др.

Все события, заключающиеся в том, что в n испытаниях событие A произошло x раз, а событие произошло n-x раз, являются несовместными. Поэтому для вычисления вероятности объединения этих событий (или суммы этих событий), нужно сложить вероятности всех этих событий, каждая из которых равна pⁿq^n-x . Всего таких событий можно насчитать столько, сколько можно образовать различных последовательностей длины n, содержащих x цифр "1" и n-x цифр "0". Таких последовательностей получается столько, сколькими способами можно разместить x цифр "1" (или n-x цифр "0") на n местах, то есть число этих последовательностей равно

Обозначение. P_n(x) – вероятность того, что в схеме Бернулли, состоящей из n испытаний, произошло ровно х успехов.

Отсюда получается формула Бернулли:

P_n(x) =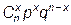

По формуле Бернулли рассчитывается вероятность появления события A "x"раз в n повторных независимых испытаниях, где p - вероятность появления события A в одном испытании (успе ха), q - вероятность появления события в одном испытании (неудачи) , p+q=1.

Замечание 19.5. Очевидно, что формулу Бернулли удобно использовать для относительно небольшого числа испытаний. При большом n вычисления становятся затруднительными.

Определение 19.1.1. Сформулированные условия проведения испытаний иногда называются "схемой повторных независимых испытаний" или "схемой Бернулли". Итак, последовательность испытаний называется схемой Бернулли, если:

1) испытания независимы

2) в каждом испытании возможны только 2 исхода – успех (некоторое событие А происходит) и неудача (событие А не происходит)

3) вероятность успехов и неудач в каждом испытании постоянна. Вероятность успеха обозначается p, вероятность неудачи – q, а p+q = 1

Пример 19.1.1.Самым простым примером схемы Бернулли является многократное подбрасывание монеты, где за успех принято выпадение «герба» или «решетки».

Пример 19.1.2. Из урны, содержащей 2 белых и 6 черных шаров наудачу выбирается с возвращением 5 раз подряд один шар. Подсчитать вероятность того, что 4 раза появится белый шар.

В приведенных выше обозначениях n=8; p=1/4; q=3/4; x=5. Искомую вероятность вычисляем по формуле Бернулли:

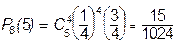
Пример 19.1.3.

Вероятность выигрыша на один лотерейный билет равна 0,01. Определим, сколько билетов нужно купить, чтобы вероятность хотя бы одного выигрыша в лотерее была не менее заданного значения Р_з = 0,9.

Пусть куплено n билетов. Предположим, что общее число билетов, разыгрывающихся в лотерее велико (во много раз больше купленных билетов). При этом можно считать, что каждый билет выигрывает независимо от остальных с вероятностью р = 0,01. Тогда вероятность получить к выигрышных билетов можно определить, используя формулу Бернулли. В частности, имеем при q = 1 — р:

Р{к ≥ 1} = 1 - qⁿ = 1 – (1 - р)ⁿ ≥ Р_з,

откуда получаем

n ≥ ln (1 – P) / ln (1 – p) = ln 0,1 / ln 0,99 ≈ 230

Таким образом, нужно купить не менее 230 лотерейных билетов.

По формуле Бернулли можно подсчитать вероятности всех возможных частот: x=0,1,2,3,4,5.

Формула Бернулли при заданных числах p и n позволяет рассчитывать вероятность любой частоты x (0 £ x £ n). Возникает естественный вопрос: какой частоте будет соответствовать наибольшая вероятность?

Предположим, что такая частота существует, и попытаемся ее определить из условия, что вероятность этой частоты не меньше вероятности "предыдущей" и "последующей" частот:

P_n(x) ³ P_n (x-1);

P_n(x) ³ P_n (x+1)

Первое неравенство представляется в виде:

,

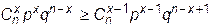что эквивалентно 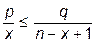или 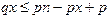. Отсюда следует:

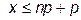
Решая второе неравенство, получим

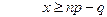
Таким образом, частота, имеющая наибольшую вероятность (чем вероятнейшая частота), определяется двойным неравенством

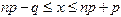
Если np + p – целое число (тогда и np – q – целое число), то две частоты: x=np – q и x=np + p обладают наибольшей вероятностью. Например, при 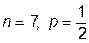, наивероятнейшие частоты: x = 3; x = 4.