Вторая интерполяционная формула Ньютона

Вторая интерполяционная формула Ньютона применяется, когда значение аргумента ближе к концу отрезка интерполяции (формула для интерполирования назад). Интерполяционный многочлен ищется в виде многочлена n-ой степени:

P_n(x) = a₀+ a₁(x-x_n) + a₂(x-x_n)(x-x_n-1) +…+ a_n(x-x_n)…(x-x₁) (4)Коэффициенты a₀, a₁, …, a_n находятся из условия совпадения значения исходной

функции f(x) и интерполяционного многочлена P (x) в узлах: a

=

Dk yn-k

.

k

n

k!hk

x - xn

Подставив

ak в(4)

и перейдя

к переменной t =

, получим вторую

h

интерполяционную формулу Ньютона:

Pn (x)= Pn (xn

+ th)= yn + tDyn-1+

t(t +1)

D2 yn-2

+ ... +

t(t +1)...(t + n -1)

Dn y0.

2!

n!

Погрешность вычислений оценивается следующим образом:

R (x)

»

t(t +1)(t +2)...(t + n)

Dn+1 y .

n

(n +1)!

Рассмотрим задачу субтабулирования (уплотнения таблицы) функции на отрезке.

Введем следующие обозначения:

a, b – концы субтабулирования;

H0 – старый шаг таблицы;

H – новый шаг таблицы;

y1, y2, y3 – конечные разности 1-го, 2-го, 3-го порядка; d – границы погрешности метода.

Для вычисления конечных разностей составляется таблица:

xi	yi=sin xi	D yi	D2 yi	D3 yi
0,150	0,14944	0,00494	0,00000	-0,00001
0,155	0,15438	0,00494	-0,00001	0,00001
0,160	0,15932	0,00493	0,00000	0,00000
0,165	0,16425	0,00493	0,00000	-0,00001
0,170	0,16918	0,00493	-0,00001
0,175	0,17411	0,00492
0,180	0,17903

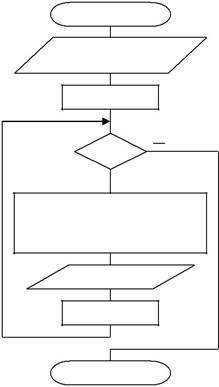
начало

Блок-схема уплотнения таблиц функций:

Ввод a, b, h0, h,

x:=a

x≤b

+

t:=(x-a)/h0

y:=y0+t*y1+t*(t-1)*y2/2

Вывод x, y, d

x:=x+h

конец

Программа уплотнения таблиц функций (субтабулирования)

program subtab;

var a,b,d,h0,h,y,y0,y1,y2,y3,x,t : real;

begin

writeln;

write('Введите a, b, H0, H - ');

readln(a,b,H0,H);

write('Введите Y0, конечные разности Y1, Y2, y3 - '); readln(Y0,Y1,Y2,y3);

writeln(' X Y

x:=a;

while x<=b do

begin t:=(x-a)/h0;

D');

y:=y0+t*y1+t*(t-1)*y2/2;

d:=y3*t*(t-1)*(t-2)/6;

writeln(x:8:4, y:12:6, d:14:8);

x:=x+h

end;

readln;

end.

Введите a, b, H0, H - 0.155 0.165 0.005 0.001 Введите Y0, конечные разности Y1, Y2, y3 –

0.15438	0.00494 -0.00001 0.00001
X	Y	D
0.1550	0.154380	0.00000000
0.1560	0.155369	0.00000048
0.1570	0.156357	0.00000064
0.1580	0.157345	0.00000056
0.1590	0.158333	0.00000032
0.1600	0.159320	0.00000000
0.1610	0.160307	-0.00000032
0.1620	0.161293	-0.00000056
0.1630	0.162279	-0.00000064
0.1640	0.163265	-0.00000048
0.1650	0.164250	-0.00000000

Численное интегрирование. Квадратурные формулы Ньютона-Котеса.

Численное интегрированиеДля вычисления определенного интеграла используется

b

формула Ньютона-Лейбница: ò f (x)dx = F (b) - F (a) ,

a

где F(x) – одна из первообразных функции f(x) (такая что F’(x)=f(x)).

Однако функция f(x) может быть задана таблицей или графиком, а также аналитически, но нахождение первообразной в аналитическом виде затруднительно. В этих случаях применяют методы приближенного (численного) интегрирования.

Формулы, используемые для приближенного вычисления однократных интегралов, называют квадратурными формулами.

b

b

Считая f(x)» Ln(x), на [a,b], получим ò f (x)dx »ò Ln (x)dx

a

a

b

n

(x - x0 )...(x - xn )

ò f (x)dx »òå yi

dx

=

[(xi - x0 )...(xi

- xi-1)(xi

a

i=0

- xi+1)...(xi - xn )](x - xi )

n

b

(x - x0 )...(x - xn )

=å yi

ò

dx

[(x

i

- x

)...(x

i

- x

i

-1

)(x

i

- x

i+1

)...(x

i

- x

n

)](x - x

)

i=0

a

i

не зависит от x, обозначим через Ai

Перейдем всюду к переменной t:

x - x0

= t ,откуда dt =

dx

, dx = hdt =

b - a

dt .

h

h

n

При

x = x0

t = 0;

…

x = xn

t =

xn - x0

= n .

h

Тогда

A =

b - a n (-1)n-i t(t -1)...(t - n)

dt .

ò

i

n

i! (n - i)! (t - i)

Таким образом, A =(b-a) H , где H

=

1 n

(-1)n-i t(t -1)...(t - n)

dt , i=0,1,…,n.

i

n ò

i

i

i! (n - i)! (t - i)

b

ò f (x)=(b - a)å y_i H _iⁿ

_a i=0

{

}