Остойчивость при больших наклонениях
Вводные замечания
Остойчивость судов при продольных наклонениях, как правило, лежит в пределах применимости метацентрической формулы остойчивости (метода начальной остойчивости). При больших углах дифферента (y > 10°) для определения осадки в оконечностях судна может быть использована диаграмма осадок носом и кормой [3] или диаграмма их изменения [1].
При поперечных наклонениях судов угол крена нередко достигает значений, при которых метацентрическая формула не дает действительной зависимости восстанавливающего момента от угла наклонения.
Остойчивость большинства судов в поперечной плоскости является минимальной. Известные случаи потери остойчивости свидетельствуют, что опрокидывание судов происходит в плоскости близкой к поперечной. Остойчивость судна при больших углах крена является предметом одной из важнейших задач по обеспечению его безопасности – недопущению опрокидывания.
В соответствии с отмеченным, ниже рассматриваются наклонения судна только в поперечной плоскости.
При равнообъемных наклонениях (V= const) в поперечной плоскости ось поворота (продольная ось) судна смещается, по мере увеличения угла крена, в сторону борта наклонения. При большом значении угла крена (q1, рис. 3.1) ось поворота проходит через центр тяжести площади ватерлинии ВЛ1; положение этой оси на рис. 3.1 задано точкой 01. Для сравнения, в методе начальной остойчивости (при малых углах наклонения, см. п. 2.2) положение оси наклонения судна принято (условно) неизменным (по рис. 3.1 – точка 0).
Другим базовым фактором, отличающим метод остойчивости при больших углах крена от метода начальной остойчивости, является учет изменения момента инерции площади равнообъемных ватерлиний от угла крена (для ВЛ0 момент инерции 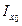 , для ВЛ1 –
, для ВЛ1 – 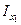 , см. рис. 3.1). По методу начальной остойчивости (см. п.2.1.2) принято:
, см. рис. 3.1). По методу начальной остойчивости (см. п.2.1.2) принято: 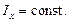
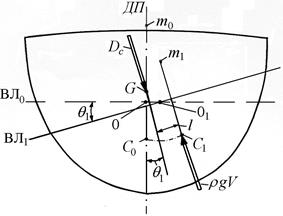 |
Рис. 3.1. плечо статической остойчивости при больших наклонениях
Изменение момента инерции площади ватерлинии вызовет изменение величины метацентрического радиуса (на рис. 3.1: 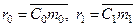 ) и положения метацентра (точки m0, m1). Соответственно изменяется и радиус кривизны траектории центра величины (траектории перемещения точки С). Траектория будет отличаться от окружности, положенной в основу при выводе метацентрической формулы остойчивости.
) и положения метацентра (точки m0, m1). Соответственно изменяется и радиус кривизны траектории центра величины (траектории перемещения точки С). Траектория будет отличаться от окружности, положенной в основу при выводе метацентрической формулы остойчивости.
Отмеченные обстоятельства существенно меняют зависимость восстанавливающего момента от угла крена.
Метацентрический радиус при поперечном наклонении определяется по формуле
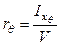 , , |
| где | 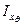 | – | центральный поперечный момент инерции площади равнообъемной ватерлинии при угле крена q; |
| V = const | – | неизменное при наклонении объемное водоизмещение. |
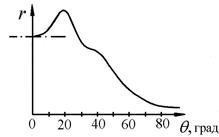 Рис. 3.2. зависимость поперечного метацентрического радиуса от угла крена Рис. 3.2. зависимость поперечного метацентрического радиуса от угла крена | Характерный вид кривой 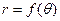 представлении на рис. 3.2. Горизонтальная касательная при θ = 0 (рис. 3.2) незначительно отстоит от кривой при малых наклонениях (θ ≤ 10°), так как при этом слабо меняется момент инерции площади ватерлинии. представлении на рис. 3.2. Горизонтальная касательная при θ = 0 (рис. 3.2) незначительно отстоит от кривой при малых наклонениях (θ ≤ 10°), так как при этом слабо меняется момент инерции площади ватерлинии. |
Зависимость r = f(θ) полностью определяет траекторию перемещения центра величины. Она может быть рассчитана в координатах «y–z» с использованием зависимостей
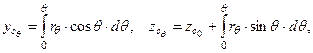 | ||||
| где | 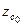 | – | аппликата центра величины при q = 0. |
При известных значениях 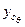 и
и 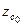 координаты соответствующего метацентра определяются по формулам
координаты соответствующего метацентра определяются по формулам
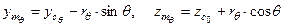 . . |
Траектории перемещения центра величины (C) и метацентра (т) принято представлять на «полярной диаграмме поперечной остойчивости», которая представляет собой специальное геометрическое построение. Полярная диаграмма служит для комплексного представления зависимостей пяти параметров остойчивости от угла крена (подробнее см. [4]);зависимости по трем основным параметрам даны на рис. 3.3.
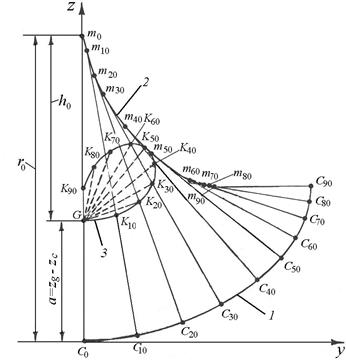 |
Рис. 3.3. Кривая центров величины (1), кривая метацентров (2),
полярная диаграмма статической остойчивости (3)
На рис. 3.3 принято: кривая центров величины начинается от точки С0, кривая метацентров – от точки т0, число – индекс у буквенного обозначения показателя представляет значение угла крена. Отрезок прямой, соединяющий соответствующие точки 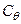 и
и 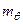 , перпендикулярен к плоскости ватерлинии и определяет направление действия силы поддержания (
, перпендикулярен к плоскости ватерлинии и определяет направление действия силы поддержания ( 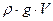 ).
).
Зная положение соответствующих точек 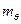 и
и  графическим методом можно получить плечо момента восстанавливающего при заданном значении угла крена или, что тоже, плечо статической остойчивости при заданном наклонении (например, отрезок
графическим методом можно получить плечо момента восстанавливающего при заданном значении угла крена или, что тоже, плечо статической остойчивости при заданном наклонении (например, отрезок 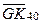 на рис. 3.3). Совокупность таких плеч на рис. 3.3 дана в форме полярной диаграммы статической остойчивости.
на рис. 3.3). Совокупность таких плеч на рис. 3.3 дана в форме полярной диаграммы статической остойчивости.
Полярная диаграмма поперечной остойчивости, фрагмент которой представлен на рис. 3.3, дает комплексное и наглядное представление о совокупности показателей остойчивости. Полярная диаграмма удобна для выполнения анализа остойчивости, но неудобна для решения задач по остойчивости, возникающих в практике судоходства.
В производственных условиях, в качестве «инструмента» для выполнения расчетов по остойчивости при больших углах крена, используются диаграмма статической остойчивости и диаграмма динамической остойчивости. Такие диаграммы и возможности их применения представлены ниже.
