III. Уравнения движения оболочек

Если отнести оболочку к системе гауссовых координат 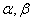, совпадающих с линиями кривизны срединной поверхности, то уравнения движения могут быть записаны в таком виде:

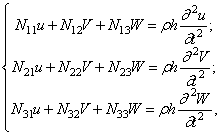
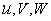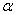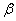где - компоненты перемещения точки срединной поверхности в направлениях - и -линий и по нормали;

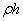- масса оболочки на единицу срединной поверхности;

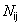- дифференциальные операторы.

Структура операторов 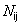для оболочек произвольной формы весьма сложна. Поэтому уравнения движения в перемещениях имеет смысл записывать только для простейшего случая цилиндрической оболочки постоянной толщины, для которой коэффициенты уравнений постоянны. В этом случае

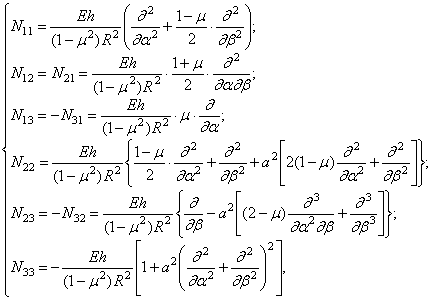
где 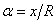; 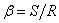- безразмерные координаты точки на срединной поверхности; .

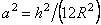Система уравнений имеет восьмой порядок по координатам 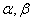и второй - по времени 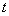. Даже тогда, когда эти уравнения имеют постоянные коэффициенты (т.е. для цилиндрической оболочки) и при рассмотрении гармонических колебаний с частотой 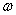, т.е. при

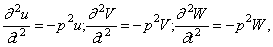
аналитическое решение этих уравнений может быть получено лишь при некоторых специально подобранных граничных условиях. В остальных случаях для расчета используют приближенные или численные методы.

Особенностью уравнений движения оболочек является то, что в эти уравнения входит малый, пропорциональный квадрату толщины оболочки, параметр 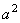, на который умножаются старшие производные перемещений по координатам. Поэтому, если рассматриваются такие формы колебаний, при которых перемещения медленно меняются по координатам 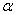и 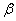, соответствующими моментными членами в уравнениях можно пренебречь. На основе безмоментной теории рассматривают низшие формы колебаний оболочек, закрепленных так, что обеспечивается возможность безмоментного состояния.

При высших формах собственных колебаний оболочка разбивается узловыми линиями на ряд достаточно пологих сегментов, на каждом из которых напряженное состояние быстро изменяется по координатам. В этом случае для расчета может быть использована так называемая теория пологих оболочек. Применительно к цилиндрической оболочке уравнения теории пологих оболочек получаются из уравнений, если в операторах 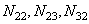опустить слагаемые с множителем .

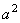Аналитическое решение задачи о собственных колебаниях для замкнутой цилиндрической оболочки может быть получено при так называемых граничных условиях Навье. Согласно этим условиям, на торцах оболочки отсутствуют нормальные 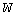и окружные 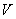перемещения, а также продольная сила 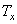в срединной поверхности и изгибающий момент 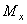. Условиям Навье удовлетворяют следующие выражения компонентов перемещения:

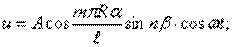
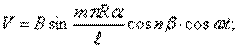
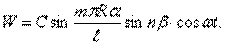
Подставив эти выражения в уравнения движения, придем к системе трех линейных алгебраических уравнений относительно .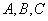

Равенство нулю определителя этой системы приводит к кубическому уравнению относительно 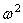. Три корня этого уравнения соответствуют трем различным формам колебаний с одинаковыми числами узловых окружностей и образующих, но с различными соотношениями между .

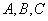В отличие от пластинок, где наименьшие собственные частоты соответствуют формам колебаний без узловых линий, в оболочках, закрепленных так, что деформация их без растяжения срединной поверхности невозможна, наименьшие частоты имеют колебания с узловыми линиями. Это объясняется тем, что формы колебаний без узловых линий связаны со значительными деформациями в срединной поверхности оболочки.

Вопросы для самоконтроля

1. Дайте определение следующих понятий

· оболочка

· пластина

· сферическая (или коническая, или цилиндрическая) оболочка

· осесимметричная (симметричная) оболочка

2. Напишите выражения для вычисления собственных частот изгибных колебаний прямоугольных пластин

3. Напишите выражения для вычисления собственных форм изгибных колебаний прямоугольных пластин

4. Напишите выражения для вычисления собственных частот колебаний круговых цилиндрических оболочек

5. Напишите выражения для вычисления собственные формы колебаний круговых цилиндрических оболочек

6. Сформулируйте краевые условия Навье-Стокса

Литература

а) основная литература

1. Бидерман, В.Л. Теория механических колебаний : Учеб. для вузов .— М., Ижевск : РХД, 2009 .— 407 с. : ил. — Библиогр.: с. 403-404.
2. Молотков, Н.Я. Механические колебания : Учеб. пособие для студентов специальностей 170500, 170600, 101600, 311300, 311900, 311400 / Н.Я. Молотков, О.В.Ломакина ; Тамбов. гос. техн. ун-т .— Тамбов : ТГТУ, 2007 .— [86]с. : ил. — Библиогр.: с. [85].

б) дополнительная литература

1. Дарков, А.В. Строительная механика : Учеб. для вузов / А.В. Дарков, Н.Н. Шапошников .— 12-е изд., стер. — СПб. : Лань, 2010 .— 655 с. : ил., табл., граф. — Библиогр.: с.650.
2. Александров, А. В. Строительная механика : Учеб. пособие для вузов ж.-д. трансп. : В 2 кн. Кн. 2. Динамика и устойчивость упругих систем / А. В. Александров, В. Д. Потапов, В. Б. Зылев ; Под ред. А. В. Александрова .— М. : Высшая школа, 2008 .— 383 с. : ил., табл., граф .— (Строительство и архитектура) .— Библиогр.: с. 380-381.
3. Бирбраер, А. Н. Динамика знаний и сооружений. Воздействие ветра на сооружения : Учеб. пособие / С.-Петерб. гос. политехн. ун-т .— СПб : Изд-во Политехн. ун-та, 2008 .— 113 с. : ил., табл. — Библиогр.:с.112-113.
4. Игнатьев, В.А. Основы строительной механики : Учебник / В.А. Игнатьев, В.В. Галишникова ; Волгогр. гос. архит.-строит. ун-т .— Волгоград : ВолгГАСУ, 2007 .— 637 с. : ил. — Библиогр.: с. 626-628.