II. Колебания оболочек без растяжения срединной поверхности

На основе описанной выше теории рассмотрим колебания цилиндрической оболочки. Определим положение произвольной точки 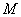на срединной поверхности оболочки координатами 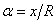и .

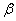Компоненты перемещения точки в продольном, окружном и нормальном к поверхности направлениях обозначим соответственно 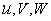. Компоненты деформации срединной поверхности определяются формулами

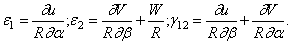
Приравняв 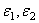и 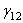нулю и проинтегрировав полученные уравнения, выразим 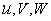через две произвольные функции угловой координаты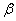

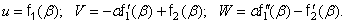
Из полученных формул видно, что при деформации цилиндрической оболочки без растяжения срединной поверхности образующие остаются прямыми, а осевые перемещения не зависят от продольной координаты.

Формулы показывают, что чистые изгибания замкнутой цилиндрической оболочки возможны в следующих случаях:

а) если ее торцы свободны; в этом случае отличны от нуля 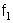и ;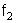

б) если на одном из торцов запрещены перемещения 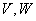, но разрешено перемещение ;

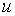в) если на одном из торцов запрещено перемещение 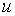. Если же оболочка оперта на обоих торцах, чистое изгибание ее невозможно.

Составим выражения потенциальной и кинетической энергии оболочки, совершающей гармонические колебания с частотой 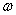. В общем выражении потенциальной энергии деформации сохраняется только слагаемое 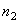. Входящие в него параметры изменения кривизны определяются формулами

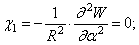
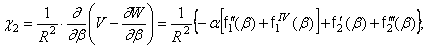
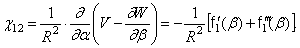
После подстановки этих значений в выражение 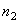и интегрирования по 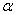с учетом того, что , находим

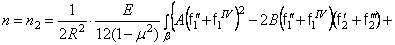
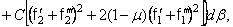(346)

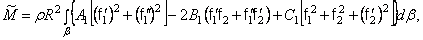
где

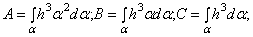
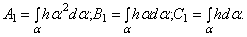
Интегралы в выражениях 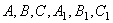вычисляются по всей длине оболочки.

Из основного уравнения метода Рэлея-Ритца следует, что выражени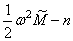е (где 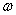- частота собственных колебаний) должно иметь стационарное значение:

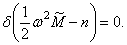
Отсюда следует система обыкновенных дифференциальных уравнений для функции 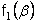, 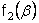. В этом случае, если форма всех меридиональных сечений одинакова (толщина оболочки не зависит от 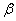), коэффициенты 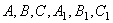постоянны и уравнения получают такой вид:

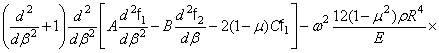
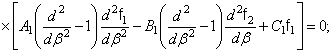(347)

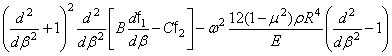
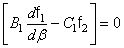. (348)

Решение этих дифференциальных уравнений для открытых оболочек должно быть подчинено граничным условиям на продольных кромках. На этих кромках могут быть заданы перемещения 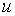(постоянные вдоль каждой кромки), а также перемещения 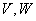и угол поворота

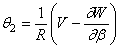
в двух различных сечениях по длине оболочки. Всего имеется семь кинематических граничных условий на каждой продольной кромке, что соответствует четырнадцатому порядку уравнений. Если закрепления отсутствуют, то кинематические граничные условия заменяются естественными граничными условиями.

Если оболочка симметрична относительно поперечного сечения 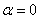(рис.а), то 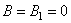и функции 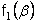, 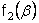определяются независимыми дифференциальными уравнениями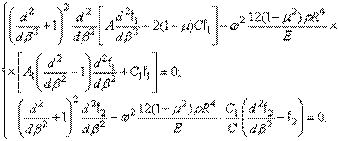

Функция 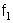описывает в этом случае кососимметричные относительно сечения 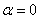формы колебаний, а функция 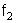- симметричные.

Уравнение, определяющее функцию 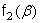, совпадает с уравнением колебаний кольца в своей плоскости.

Для замкнутой оболочки граничные условия заменяются условиями периодичности, которым удовлетворяют функции 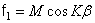, 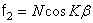. В случае симметричной оболочки подстановка этих выражений в уравнения приводит к следующим значениям частот для кососимметричных колебаний:

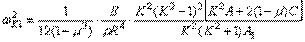
и для симметричных колебаний:

.

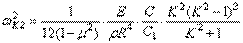Для оболочки постоянной толщины 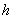и длины 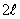(рис.б):

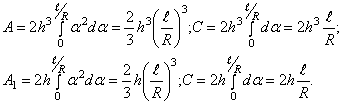
В этом случае

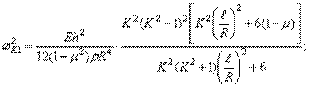
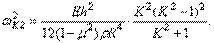
Как видно из полученных формул, при колебаниях оболочек без растяжения срединной поверхности частоты определяются зависимостями такого же типа, как и для пластинок. При стремлении толщины оболочки к нулю частота ее колебаний без растяжения срединной поверхности также стремится к нулю.