Название раздела содержания: Рациональные числа Объект оценивания: Распознавание различных видов числа
Задание № 2
Название раздела содержания: Рациональные числа Объект оценивания: Распознавание различных видов числа
1) Соотнесите обыкновенные дроби с равными им десятичными
А)  ; Б)
; Б) 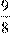 ; В)
; В) 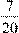
1) 0,6; 2) 1,125; 3) 0,35; 4) 4,5
| А | Б | В |
2) Соотнесите обыкновенные дроби с равными им десятичными
А) 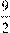 ; Б)
; Б) 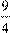 ; В)
; В) 
1) 0,28; 2) 1,2; 3) 2,25; 4) 4,5
| А | Б | В |
3) Из чисел: 6; -5; 8,3; - 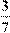 ; -5
; -5 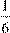 ; -100; -0,37;
; -100; -0,37;  ; 6
; 6 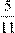 ; -2; 1000 выберите и выпишите
; -2; 1000 выберите и выпишите
1) целые числа
2) целые отрицательные числа
3) целые положительные числа
4) дробные числа
5) отрицательные дробные числа
6) положительные дробные числа
7) отрицательные десятичные дроби
8) положительные десятичные дроби
9) натуральные числа
4) На координатной прямой изображено число а , соответствующее точке А. Выберите верное утверждение
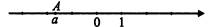
1) Число а натуральное
2) Число а положительное
3) Число а отрицательное
4) Число а целое положительное
5) Число а целое отрицательное
5) На координатной прямой изображено число а , соответствующее точке А. Выберите верное утверждение
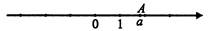
1) Число а натуральное
2) Число а положительное
3) Число а отрицательное
4) Число а целое положительное
5) Число а целое отрицательное
6) На координатных прямых отмечены точки М , N , P . Выберите верное утверждение
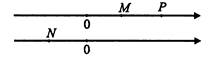
1) Координаты точек М , N являются положительными числами
2) Координаты точек М , P являются положительными числами
3) Координаты точек М , N являются отрицательными числами
4) Координата точки N является отрицательным числом
7) Сколько целых чисел расположено на координатной прямой между числами (-3) и 8
1) 10 2) 12 3) 9 4) 7
8) Сколько натуральных чисел расположено на координатной прямой между числами (-2) и 5
1) 8 2) 5 3) 6 4) 4
Задание № 3
Название раздела содержания: Уравнения Объект оценивания: Решение простейших уравнений
Решите уравнение
1) 4x+3= 2x
2) 7x -3= 6x
3) (-7-3x)=10x -2
4) -8x + 2(9+7x) = 5x -10
5) 8x +6(-5-7x)= 6x + 4
6) - x + 2(7-2x)= -10x +3
7) -5(-9+3x)-5x = -10
8) x +7(10 – x) = -2x + 2
9) x +1-5(x-5)= 5(5- x)+5
10) 3(10-7x)- x = -3
11) 4(8+7x)-10x =8
Задание № 4
Название раздела содержания: Координатная плоскость Объект оценивания: Определение координат точки, отмеченной на координатной плоскости
1) Определите координаты точки пересечения прямых АВ и СК
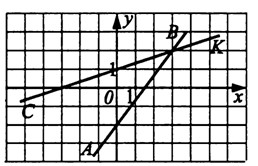
1) (3;2) 2) (-3;0) 3) (2;3) 4) (0;-2)
2) Выберите точку, абсцисса которой равна 5
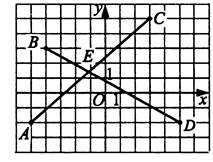 1) А 2) В 3) С 4) D
1) А 2) В 3) С 4) D
3) Определите координаты точки пересечения прямых АВ и СD
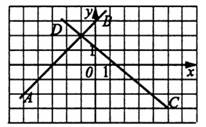
1) (1;3) 2) (-1;2) 3) (2;-1) 4) (-1;-2)
4) Определите координаты точки пересечения прямых MN и KE
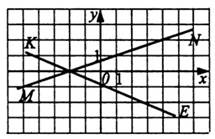
1) (0;-2) 2) (2;0) 3) (-2;0) 4) (0;2)
5) Определите координаты точки пересечения прямой MN с осью Oy
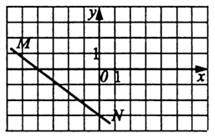
1) (0;-3) 2) (-4;0) 3) (-3;0) 4) (0;-4)
6) Определите координаты точки пересечения прямой AB с осью Ox
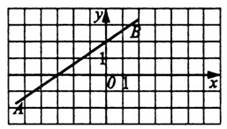
1) (0;-3) 2) (-3;0) 3) (3;0) 4) (0;2)
7) Определите координаты точки пересечения прямых PQ и EF

1) (-6;3) 2) (-3;3) 3) (-3;0) 4) (-6;0)
8) Определите координаты точки пересечения прямых AB и MN
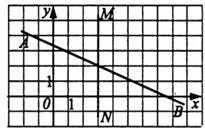
1) (2;3) 2) (3;2) 3) (0;2) 4) (3;0)
9) Определите координаты точки пересечения отрезка AB с осью ординат

1) (2;0) 2) (0;2) 3) (0;4) 4) (4;0)
10) Определите координаты точки пересечения отрезка AB с осью абсцисс

1) (2;0) 2) (0;2) 3) (0;2,5) 4) (-2;0)
11) Определите координаты точки диагоналей четырехугольника ABCD
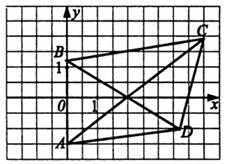
1) (2;0) 2) (3;-1) 3) (0;1) 4) (0;-2)
12) Определите координаты точки диагоналей четырехугольника MNPQ
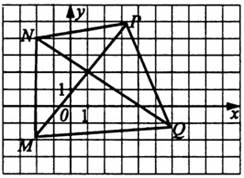
1) (1;2) 2) (3;0) 3) (2;1) 4) (0;2)
13) Определите координаты вершины треугольника ABC , которая лежит на оси абсцисс

1) (0;-1) 2) (4;0) 3) (-2;0) 4) (0;3)
14) Определите координаты вершины треугольника ABC , которая лежит на оси ординат

1) (0;-1) 2) (4;0) 3) (-2;0) 4) (0;3)
15) В пятиугольнике MNKPC определите координаты вершины K
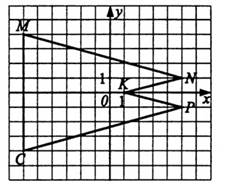 1) (1;1) 2) (0;1) 3) (1;0) 4) (0;-1)
1) (1;1) 2) (0;1) 3) (1;0) 4) (0;-1)
16) В четырехугольнике ABCD определите координаты вершины B

1) (0;2) 2) (2;0) 3) (2;2) 4) (2;1)
17) Определите координаты центра окружности

1) (1;2) 2) (2;1) 3) (0;1) 4) (2;0)
Задание № 5 Название раздела содержания: Рациональные числа Объект оценивания: Сравнение и упорядочивание дробей
1) Укажите выражение, значение которого является наименьшим.

2) Запишите в ответе номера выражений, значения которых положительны.

3) Расположите в порядке возрастания числа 0,1439; 1,3; 0,14.
1) 0,1439; 0,14; 1,3 2) 1,3; 0,14; 0,1439 3) 0,1439; 1,3; 0,14 4) 0,14; 0,1439; 1,3
4) Расположите в порядке убывания числа 0,1327; 0,014; 0,13.
1) 0,1327; 0,014; 0,13 2) 0,014; 0,13; 0,1327
3) 0,1327; 0,13; 0,014 4) 0,13; 0,014; 0,1327
5) Расположите числа в порядке возрастания: -0,5; (-0,5)2; (-0,5)3
1) -0,5; (-0,5)2; (-0,5)3 2) -0,5; (-0,5)3; (-0,5)2
3) (-0,5)3; -0,5; (-0,5)2 4) (-0,5)2; (-0,5)3; -0,5
6) Расположите числа в порядке возрастания: 
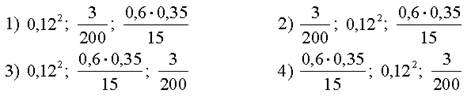
7) Укажите наибольшее из следующих чисел:
1) 0,7 2) 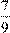 3)
3)  4)
4) 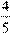
8) Укажите наименьшее из следующих чисел:
1) 0,7 2)  3)
3)  4)
4) 
9) Укажите выражения, значения которых равны 0,25. Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.

10) Среди чисел 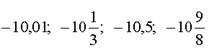 выберите наибольшее
выберите наибольшее
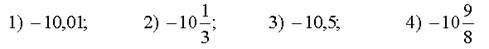
Задание № 6 Название раздела содержания: Алгебраические выражения Объект оценивания: Упрощение буквенных выражений. Вычисление значения буквенных выражений при заданных значениях букв
1) Найдите значение выражения – x+3y - z при x = 0,5; y = - 0,9 ; z = -1,6
2) Найдите значение выражения 3x + y + 2z при x = -1,1; y = 0,1; z =1,1
3) Найдите значение выражения  при x = 6,2; y = -8,2; z = -0,5
при x = 6,2; y = -8,2; z = -0,5
4) Найдите значение выражения 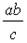 при a = 5,4; b = 3,4; c = 0,45
при a = 5,4; b = 3,4; c = 0,45
5) Найдите значение выражения  при x = - 2,9; a = - 1,9
при x = - 2,9; a = - 1,9
6) Упростите выражение 36,2a - 19a + 3 + 1,5a и найдите его значение, если a =10
7) Упростите выражение 5,8m + 4,86m + 3,6m - 2m и найдите его значение, если m = 0,1
Задание № 7 Название раздела содержания: Рациональные числа Объект оценивания: Сравнение рациональных чисел
1) Запишите в ответе номера выражений, значения которых отрицательны

2) Запишите в ответе номера выражений, значения которых положительны
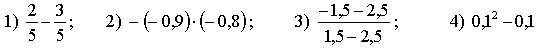
3) Сравните значения выражений и в ответ запишите наименьшее значение:

4) Сравните значения выражений и в ответ запишите наибольшее значение:

5) Укажите номер выражения, значение которого является наименьшим

6) Укажите номер выражения, значение которого является наименьшим

7) Укажите номер выражения, значение которого является наименьшим

8) Среди чисел 0,007; |-5,7|; -2,1; -3,5 выберите наименьшее
1) 0,007; 2) |-5,7|; 3) -2,1; 4) -3,5
Задание № 8 Название раздела содержания: Наглядная геометрия
Задание № 9 Название раздела содержания: Измерения, приближения, оценки Объект оценивания: Умение переходить от одних единиц измерения величин к другим. Умение интерпретировать ответ задачи в соответствии с поставленным вопросом
1) Сырок стоит 7 рублей 20 копеек. Какое наибольшее число сырков можно купить на 60 рублей?
2) Теплоход рассчитан на 750 пассажиров и 25 членов команды. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды?
3) В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 1200 листов. Какого наименьшего количества пачек бумаги хватит на 4 недели?
4) Больному прописано лекарство, которое нужно принимать по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
5) Для приготовления маринада для огурцов на 1 литр воды требуется 12 г лимонной кислоты. Лимонная кислота продается в пакетиках по 10 г. Какое наименьшее число пачек нужно купить хозяйке для приготовления 6 литров маринада?
6) В летнем лагере на каждого участника полагается 40 г сахара в день. В лагере 166 человек. Сколько килограммовых пачек сахара понадобится на весь лагерь на 5 дней?
Задание № 10 Название раздела содержания: Отношение величин Объект оценивания: Использование понятия «отношение» при решении задач
1) Туристическая фирма организует трёхдневные автобусные экскурсии. Стоимость экскурсии для одного человека составляет 3500 р. Группам предоставляются скидки: группе от 3 до 10 человек — 5%, группе более 10 человек — 10%. Сколько рублей заплатит за экскурсию группа из 8 человек?
2) В период распродажи магазин снижал цены дважды: в первый раз на 30%, во второй – на 50%. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 700 р.?
3) Городской бюджет составляет 45 млн рублей, а расходы на одну из его статей составили 12,5%. Сколько рублей потрачено на эту статью бюджета?
4) Сберегательный банк начисляет на срочный вклад 20% годовых. Вкладчик положил на счет 800 р. Сколько рублей будет на этом счете через год, если никаких операций со счетом проводиться не будет?
5) На счет в банке, доход по которому составляет 15% годовых, внесли 24 тыс. р. Сколько тысяч рублей будет на этом счете через год, если никаких операций со счетом проводиться не будет?
6) Товар на распродаже уценили на 20%, при этом он стал стоить 680 р. Сколько рублей стоил товар до распродажи?
Задание № 11
Задание № 12
Задание № 13 Название раздела содержания: Описательная статистика Объект оценивания: Вычисление среднего арифметического величин
1) Василий измерял в течение недели время, которое он тратил на дорогу до школы, а результаты записывал в таблицу.
| День недели | Пн | Вт | Ср | Чт | Пт | Сб |
| Время (мин) |
Сколько минут в среднем занимает у Василия дорога до школы?
2) Василий измерял в течение недели время, которое он тратил на дорогу до школы, а результаты записывал в таблицу.
| День недели | Пн | Вт | Ср | Чт | Пт | Сб |
| Время (мин) |
Сколько минут в среднем занимает у Василия дорога до школы?
3) . В разновозрастной группе театрального кружка занимается 8 школьников. Записали возраст каждого: 12 лет, 14 лет, 13 лет, 9 лет, 9 лет, 13 лет, 14 лет, 12 лет. Вычислите средний возраст школьников, занимающихся в театральном кружке.
4) Записана высота (в см) пяти саженцев-трехлеток яблони сорта "Антоновка": 147, 140, 136, 153,
134. Вычислите среднюю высоту этих саженцев
5) Каждые полчаса гидролог замеряет температуру воды в водоеме и получает следующий ряд значений: 12,8; 13,1; 12,7; 13,2; 12,7. Вычислите среднюю температуру воды в водоеме
6) На соревнованиях трое судей оценили выступление гимнастки оценка 5,7; 5,5; 5,6. Найти среднюю оценку выступления гимнастки
1) 5,6 2) 5,5 3) 5,7 4) 5,55
7) Среднее арифметическое четырех чисел равно 0,6, а среднее арифметическое двух других чисел равно 3,2. Найти среднее арифметическое всех этих чисел
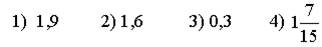
8) Среднее арифметическое четырех чисел равно 0,8, а среднее арифметическое двух других чисел равно 3,6. Найти среднее арифметическое всех этих чисел
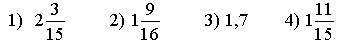
Задание № 14
Задание № 15 Название раздела содержания: Описательная статистика Объект оценивания: Извлекать необходимую информацию из диаграмм
1) Завуч школы подвел итоги по выбору предметов для сдачи ЕГЭ учащимися 11-х классов. Результаты представлены на диаграмме. Сколько примерно учащихся выбрали для сдачи ЕГЭ физику?

В ответе укажите номер правильного варианта.
1) 16 2) 12 3) 14 4) 8
2) На диаграмме показано количество посаженных деревьев и кустарников в г. Сочи за период с
2009 по 2012 гг. Определите, сколько всего было посажено зелёных насаждений за 2011 г. и 2012 г.?

В ответе укажите номер правильного варианта.
1) 10 000 2) 4 000 3) 12 000 4) 8 000
3) На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира.

Какие из следующих утверждений неверны?
1) Канада — крупнейшая по площади территории страна мира.
2) Площадь территории Индии составляет 3,3 млн км2.
3) Площадь Китая больше площади Австралии. 4) Площадь Канады больше площади США на 1,5 млн км2.
В ответе запишите номера выбранных утверждений.
4) На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1994 году. Ответ дайте в градусах Цельсия.

5) На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 2003 году. Ответ дайте в градусах Цельсия.

6) На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей среднемесячными температурами в 1973 году. Ответ дайте в градусах Цельсия.

7) На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру во второй половине 1999 года. Ответ дайте в градусах Цельсия.

8) На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру во второй половине 1973 года. Ответ дайте в градусах Цельсия.

9) На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с положительной среднемесячной температурой

10) На диаграмме показано распределение выплавки меди в 10 странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место по выплавке меди занимали США, десятое место — Казахстан. Какое место занимала Индонезия?

Часть 2
Задание № 16
Задание № 17 Название раздела содержания: Рациональные числа Объект оценивания: Умение строить и исследовать математические модели
1) Среди 210 000 жителей города  не интересуется футболом и никогда не смотрит его по телевизору, а остальные являются футбольными болельщиками. Среди футбольных болельщиков
не интересуется футболом и никогда не смотрит его по телевизору, а остальные являются футбольными болельщиками. Среди футбольных болельщиков  смотрело по телевизору финальный матч Чемпионата Европы. Сколько жителей города не
смотрело по телевизору финальный матч Чемпионата Европы. Сколько жителей города не
посмотрело этот матч?
2) Перед представлением в цирке для продажи было заготовлено некоторое количество воздушных шариков. Перед началом представления было продано  всех воздушных шариков, а в антракте – еще 15 штук. После этого осталась четверть всех шариков. Сколько шариков было первоначально?
всех воздушных шариков, а в антракте – еще 15 штук. После этого осталась четверть всех шариков. Сколько шариков было первоначально?
3) На три склада привезли 340 т сахара. Масса сахара, привезенного на второй склад, составляет 45% массы сахара, завезенного на первый склад, а масса сахара на третьем складе составляет 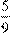
массы сахара на втором складе. Сколько тонн сахара завезли на каждый склад?
4) На трех полках 320 книг. Число книг на второй полке составляет 35% числа книг, стоящих на первой полке, а на третьей 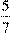 числа книг, стоящих на второй полке. Сколько книг на каждой
числа книг, стоящих на второй полке. Сколько книг на каждой
полке?
5) В первый день мотоциклисты проехали 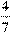 длины всего маршрута, а за второй день 15% оставшегося расстояния, после чего им осталось проехать еще 76,5 км. Какова длина намеченного маршрута?
длины всего маршрута, а за второй день 15% оставшегося расстояния, после чего им осталось проехать еще 76,5 км. Какова длина намеченного маршрута?
6) Фермер убрал урожай картофеля. 36% массы собранного картофеля было отправлено на продажу, 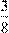 остатка отложено на хранение, а остальные 80 т были предназначены на корм скоту.
остатка отложено на хранение, а остальные 80 т были предназначены на корм скоту.
Определите массу собранного картофеля.
7) В первый день каникул мальчик прочитал 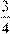 всей книги. Во второй день – 18 страниц, что составило
всей книги. Во второй день – 18 страниц, что составило  прочитанного в первый день. Сколько страниц в книге?
прочитанного в первый день. Сколько страниц в книге?
8) Шоссейные велогонки проходили в три этапа. Первый этап составил 63 км, второй –  этого
этого
расстояния, а третий – 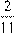 длины всей дистанции. Какова длина всей дистанции?
длины всей дистанции. Какова длина всей дистанции?
9) Покупатель заплатил за пальто  всех имеющихся у него денег, а за ботинки он заплатил 1600
всех имеющихся у него денег, а за ботинки он заплатил 1600
рублей, что составило  стоимости пальто. Сколько денег было у покупателя?
стоимости пальто. Сколько денег было у покупателя?
10) За первый час велосипедист проехал 12  км, а за второй час –
км, а за второй час –  этого расстояния, после
этого расстояния, после
чего ему осталось проехать  всего пути. Какова длина всего пути?
всего пути. Какова длина всего пути?
Задание № 2
Название раздела содержания: Рациональные числа Объект оценивания: Распознавание различных видов числа
1) Соотнесите обыкновенные дроби с равными им десятичными
А)  ; Б)
; Б) 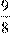 ; В)
; В) 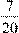
1) 0,6; 2) 1,125; 3) 0,35; 4) 4,5
| А | Б | В |
2) Соотнесите обыкновенные дроби с равными им десятичными
А) 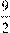 ; Б)
; Б) 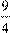 ; В)
; В) 
1) 0,28; 2) 1,2; 3) 2,25; 4) 4,5
| А | Б | В |
3) Из чисел: 6; -5; 8,3; - 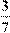 ; -5
; -5 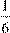 ; -100; -0,37;
; -100; -0,37;  ; 6
; 6 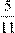 ; -2; 1000 выберите и выпишите
; -2; 1000 выберите и выпишите
1) целые числа
2) целые отрицательные числа
3) целые положительные числа
4) дробные числа
5) отрицательные дробные числа
6) положительные дробные числа
7) отрицательные десятичные дроби
8) положительные десятичные дроби
9) натуральные числа
4) На координатной прямой изображено число а , соответствующее точке А. Выберите верное утверждение
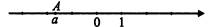
1) Число а натуральное
2) Число а положительное
3) Число а отрицательное
4) Число а целое положительное
5) Число а целое отрицательное
5) На координатной прямой изображено число а , соответствующее точке А. Выберите верное утверждение
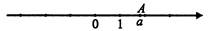
1) Число а натуральное
2) Число а положительное
3) Число а отрицательное
4) Число а целое положительное
5) Число а целое отрицательное
6) На координатных прямых отмечены точки М , N , P . Выберите верное утверждение

1) Координаты точек М , N являются положительными числами
2) Координаты точек М , P являются положительными числами
3) Координаты точек М , N являются отрицательными числами
4) Координата точки N является отрицательным числом
7) Сколько целых чисел расположено на координатной прямой между числами (-3) и 8
1) 10 2) 12 3) 9 4) 7
8) Сколько натуральных чисел расположено на координатной прямой между числами (-2) и 5
1) 8 2) 5 3) 6 4) 4
Задание № 3
