Краткие сведения о средах моделирования Matlab и Scilab
Краткие сведения о средах моделирования Matlab и Scilab
Matlab и Scilab - это популярные системы компьютерной математики, которые предназначены для выполнения инженерных и научных вычислений, таких как:
· простейшие расчеты по формулам;
· решение нелинейных уравнений и систем;
· решение задач линейной алгебры;
· решение задач оптимизации;
· дифференцирование и интегрирование;
· задачи обработки экспериментальных данных;
· решение обыкновенных дифференциальных уравнений и систем;
· моделирование непрерывных и дискретных систем.
Кроме того, пакеты предоставляют широкие возможности по созданию и редактированию различных видов графиков и поверхностей.
Работа в Matlab и Scilab
Элементы программирования на языках Matlab и Scilab
При работе в средах моделирования Matlab и Scilab существует несколько режимов:
· режим вычислений в командной строке;
· режим использования сценарных файлов. В среде Matlab создаются так называемые m-файлы, в среде Scilab используются sce- или sci-файлы. Эти файлы могут быть сохранены для дальнейшего многократного использования.
Как и система Matlab, так и система Scilab ориентированы на работу с матричными переменными. По умолчанию предполагается, что каждая заданная переменная - это матрица.
Операция присваивания
Простейшей конструкцией языков программирования Matlab и Scilab является оператор присваивания:
Имя_переменной = Выражение
Типы переменных заранее не декларируются. Они определяются выражением, значение которого присваивается переменной. Так, если это выражение - вектор или матрица, то переменная будет векторной или матричной. Имена переменных в обоих средах моделирования регистрозависимы (как в языке программирования C).
После набора оператора в командной строке и нажатия клавиши ENTER на экран дисплея выводится вычисленное значение переменной. Для блокировки вывода результата вычислений на экран оператор нужно завершить символом ; (точка с запятой).
Пример
»x=2;
»y=2;
»r=sqrt(x^2+y^2)
r=
2.8284
Возможна также конструкция, состоящая только из выражения. В этом случае для результата вычислений назначается переменная с именем ans.
Пример
»x=2;
»y=2;
»sqrt(x^2+y^2)
ans=
2.8284
В средах программирования различаются как локальные, так и глобальные переменные. При обозначении локальной переменной нет необходимости использовать какие-либо дополнительные ключевые слова, а для глобальных переменных используется ключевое слово global:
Global var
var = значение
Пример
-->global a
-->a
a =
[]
-->a=2
a =
2.
Константы
Несколько специальных функций предоставляют значения часто используемых констант в Matlab:
pi - 3.14159265...
i - мнимая единица
j - то же
eps - условный нуль
Inf - бесконечность
NaN – NotANumber, не число.
Определенные в Scilab стандартные скалярные переменные начинаются со знака %. Часть специальных переменных предопределена. Они защищены и не могут быть удалены пользователем (но могут быть переопределены).
%i - Мнимая единица
%pi - Число Pi =3.1415927
%e - Число e = 2.7182818
%eps - Это условный нуль, то есть такое максимальное число, что 1+%eps=1.
%eps=2.220E-16
%inf - Бесконечность=Inf
%nan - NotANumber: неопределено
Арифметические операции. Функции
Для выполнения арифметических операций в системах применяются обычные символы:
| Оператор | Операция |
| + | сложение |
| - | вычитание |
| * | умножение |
| / | деление |
| ^ | возведение в степень |
Эти операции являются матричными, так как применяются и при работе как и со скалярными значениями, так и с матрицами. Наряду с матричными операциями над массивами можно выполнять и поэлементные операции. Для обозначения поэлементных операций используется . (точка), предшествующая обычной (матричной) операции.
Пример:
-->x=[1 2; 3 4]
x =
1. 2.
3. 4.
-->x^2
ans =
7. 10.
15. 22.
-->x.^2
ans =
1. 4.
9. 16.
В таблице 1 приведен список основных функций сред моделирования Matlab и Scilab.
Таблица Перечень основных функций Matlab и Scilab
| Назначение функции | функция |
| Синус | sin(x) |
| Косинус | cos(x) |
| Тангенс | tan(x) |
| Арктангенс | atan(x) |
| Экспонента | exp(x) |
| Натуральный логарифм | log(x) |
| Десятичный логарифм | log10(x) |
| Квадратный корень | sqrt(x) |
| Модуль | abs(x) |
Операторы отношения и их функции
Операторы отношения служат для сравнения двух величин, векторов или матриц.
Таблица. Операторы отношения.
| Название | Оператор | Пример |
| Равно | = = | x = = y |
| He равно | ~ = | x ~ = y |
| Меньше чем | < | x<y |
| Больше чем | > | x>y |
| Меньше или равно | <= | x<=y |
| Больше или равно | >= | x>=y |
Перенос строк. Комментарии
Если для выражения не хватает одной строки или мы не желаем заходить в невидимую область окна, то выражение можно перенести на новую строку с помощью многоточия … (3 точки).
Комментарий в системе Matlab должен начинаться символом %.
В Scilab комментарий задаётся двойной косой чертой //.
Матричные операции
Создание единичной матрицы
Для создания единичной матрицы (она обычно обозначается как Е) служит функция eye:
· еуе(n) — возвращает единичную матрицу размера nxn;
· eye(m, n) — возвращают матрицу размера mxn с единицами по диагонали и нулями в остальных ячейках;
Определитель матрицы
Для нахождения определителя (детерминанта) матриц имеются следующие функции:
· det(X) — возвращает определитель квадратной матрицы X.
Построение графиков
Для построения графиков функций одной переменной y = f(x) имеется функция plot. График строится в декартовой системе координат по заданным массивам значений аргумента и функции. Заданные этими массивами точки соединяются прямыми линиями. Имеется возможность изменять тип и цвет линии и тип узловых точек (маркер). Вызов этой функции осуществляется командой:
plot(x,y,s)
в случае, если необходимо построить один график, или
plot(x1, y1, s1, x2, y2, s2, x3, y3, s3...xn, yn, sn)
для n графиков.
где x, y - одномерные массивы одинаковой размерности; x - массив значений аргумента функции у = f(x; y - массив значений функции у = f(x; s - строковая константа, определяющая цвет линии, маркер узловых точек и тип линии. Эта константа может содержать от одного до трех символов.
Строка s выглядит следующим образом
'параметр1параметр2параметр3'.
Символы пишутся один за другим без разделителей.
Параметр1 определяет цвет линии графика:
Значения параметра функции plot, определяющего цвет графика
| Символ | Описание | Символ | Описание |
| y | желтый | g | зеленый |
| m | розовый | b | синий |
| с | голубой | w | белый |
| r | красный | k | черный |
Параметр2 определяет тип маркера графика:
Значение параметра, определяющего тип маркеров (точек) графика
| Символ | Описание |
| . | точка |
| o | кружок |
| х | крестик |
| + | знак "плюс" |
| * | звездочка |
| S | квадрат |
| d | ромб |
| v | треугольник вершиной вниз |
| ^ | треугольник вершиной вверх |
| < | треугольник вершиной влево |
| > | треугольник вершиной вправо |
| p | пятиконечная звезда |
| h | шестиконечная звезда |
Параметр 3 определяет тип линии графика:
Значения параметра, определяющего тип линии графика
| Символ | Описание | Символ | Описание |
| - | сплошная | -. | штрихпунктирная |
| : | пунктирная | -- | штриховая |
Пример Matlab
% графики функций sin x, cos x
x=0:0.1:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,'k-o',x,y2,'r--*')
В результате выполнения этой программы на экран монитора будет выведено графическое окно с графиками, представленными на рис. 1.1. Графики представлены в черно-белой палитре, хотя в действительности график функции cos(x) выводится красным цветом.
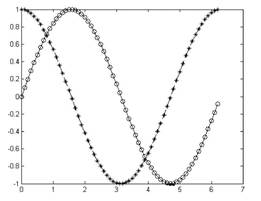
Рис. 1.1. Графики, выполненные с помощью программы plot
Структура функций Scilab
Функции играют роль подпрограмм. Удобнее всего набирать функции в текстовом редакторе и хранить их в либо в отдельных файлах (внешние функции), либо в теле основного скрипта, в начале текста (что более предпочтительно).
Синтаксис
function [y1,...,yn] = fun(x1,...,xm)
тело функции ....
Endfunction
Где
fun - имя фунции,
xi - входные аргументы функции (их m штук),
yi - выходные аргументы функции (их n штук).
Диалоговый ввод-вывод
disp(x) отображает массив, не печатая имя массива. Если x - строка, то отображается текст.
Пример
x=[1 2 3];
disp(x)
1 2 3
disp('квадрат второго элемента=')
квадрат второго элемента=
disp(x(2)^2)
r = input('введите значение') дает пользователю приглашение в текстовой строке и затем ожидает ввода с клавиатуры. Может быть введено любое Matlab(Scilab)-выражение, которое вычисляется, используя переменные в текущей рабочей области, и результат возвращается в r. Если пользователь нажимает клавишу возврата каретки, ничего не вводя, то вводится пустая матрица.
r = input(' введите значение', 's')дает приглашение в текстовой строке и ожидает ввода символьной строки. Напечатанный текст не вычисляется; символы просто возвращаются как Matlab(Scilab)-строка.
Циклы типа for-end
Циклы типа for-end обычно используются для организации вычислений с заданным числом повторений цикла. Конструкция такого цикла имеет вид:
for var = выражение
<тело цикла>
End
Выражение чаще всего записывается в виде b:s:e, где b - начальное значение переменной цикла var, s - приращение (шаг) этой переменной и e - конечное значение управляющей переменной, при достижении которого цикл завершается. Возможна запись выражения в виде b:e, в этом случае s=1. Список выполняемых в цикле инструкций завершается оператором end.
Для досрочного выполнения цикла можно использовать оператор break. Как только этот оператор встречается в программе, цикл прерывается.
Возможно использование цикла в цикле.
Пример
for i = 1:3
for j = 1:3
a(i,j) = i+j;
end
end
a
a =
2 3 4
3 4 5
4 5 6
Циклы типа while_end
While Условие
<тело цикла>
End
Цикл типа while выполняется до тех пор, пока выполняется Условие. Для прекращения выполнения цикла можно использовать оператор break.
Пример
x=1;i=1;
while x<=3
y(i)=x;
x=x+0.5; i=i+1;
end
y
y =
1.0000
1.5000
2.0000
2.5000
3.0000
Переключатель
Для осуществления множественного выбора (или ветвления) используется конструкция с переключателем:
| Matlab | Scilab |
| switch switch_Bыражение case _Bыражение Список_ инструкций case { case_Bыражение1, case_Bыражение2,… } Список_ инструкций otherwise, Список_ инструкций end | select expr0, case expr1 then instructions1, case expr2 then instructions2, ... case exprn then instructionsn, [else instructions], end |
Выполняется первый оператор case, у которого case_Bыражение соответствует switch_Bыражению. Если ни одно из case_Bыражений не соответствует switch_Bыражению, то выполняется список инструкций после оператора otherwise (если он существует). Выполняется только один case, после чего выполнение продолжается с оператора после end.
Пример Matlab
Пусть существует m-файл-сценарий swit.m:
switch month
case {1,2,3}
disp('Первый квартал')
case {4,5,6} disp('Второй квартал')
case{7,8,9} disp('Третий квартал')
case{10,11,12} disp('Четвертый квартал')
otherwise,
disp('Ошибка в данных')
end
Эта программа в ответ на значения переменной month (номер месяца) определяет номер квартала и выводит сообщение. Как это происходит, видно из следующей программы:
month=3;
swit
Первый квартал
month=10;
swit
Четвертый квартал
month=13;
swit
Ошибка в данных
Пример Scilab
while %t do
n=round(10*rand(1,1))
select n
case 0 then
disp(0)
case 1 then
disp(1)
else
break
end
end
n =
2.
Метод Крамера
Система m уравнений с n неизвестными вида:
- a11x1 + a12x2 + ... + a1nxn = b1,
- a21x1 + a22x2 + ... + a2nxn = b2,
- . . . . . . . . . . . . . . . . . . . . .
- am1x1 + am2x2 + ... + amnxn = bm,
называется системой линейных алгебраических уравнений (СЛАУ), причем xj - неизвестные , aij - коэффициенты при неизвестных , bi - свободные коэффициенты (i=1..m, j=1..n). Система из m линейных уравнений с n неизвестными может быть описана при помощи матриц: A∙x=b, где x - вектор неизвестных, A - матрица коэффициентов при неизвестных или матрица системы, b - вектор свободных членов системы или вектор правых частей . Совокупность всех решений системы (x1, x2,..., xn), называется множеством решений или просто решением системы.
Пример
Решить СЛАУ при помощи правила Крамера:
- 2x1 + x2 - 5x3 + x4 = 8,
- x1 - 3x2 - 6x4 = 9,
- 2x2 - x3 + 2x4 = -5,
- x1 + 4x2 - 7x3 + 6x4= 0.
Правило Крамера заключается в следующем. Если определитель Δ=det(A) матрицы системы из n уравнений с n неизвестными A∙x=b отличен от нуля, то система имеет единственное решение x1, x2,..., xn, определяемое по формулам Крамера: xi=Δi/Δ, где Δi - определитель матрицы, полученной из матрицы системы А заменой i- го столбца столбцом свободных членов b. Текст файла- сценария с решением задачи по формулам Крамера :
- //Матрица коэффициентов:
- A=[2 1 -5 1;1 -3 0 -6;0 2 -1 2;1 4 -7 6];
- b=[8;9;-5;0]; //Вектор свободных коэффициентов
- A1=A;A1(:,1)=b; //Первая вспомогательная матрица
- A2=A;A2(:,2)=b; //Вторая вспомогательная матрица
- A3=A;A3(:,3)=b; //Третья вспомогательная матрица
- A4=A;A4(:,4)=b; //Четвертая вспомогательная матрица
- D=det(A); //Главный определитель
- //Определители вспомогательных матриц:
- d(1)=det(A1); d(2)=det(A2); d(3)=det(A3); d(4)=det(A4);
- x=d/D //Вектор неизвестных
- P=A*x-b //Проверка
Результаты работы файла-сценария:
- x =
- 3.
- - 4.
- - 1.
- 1.
- P = 1.0D-14 *
- 0.1776357
- 0.
- - 0.0888178
- 0.1554312
- exec done
Метод обратной матрицы:
для системы из n линейных уравнений с n неизвестными A∙x=b, при условии, что определитель матрицы А не равен нулю, единственное решение можно представить в виде x=A-1∙b.
Текст файла- сценария и результаты его работы :
- //Матрица и вектор свободных коэффициентов системы:
- A=[2 1 -5 1;1 -3 0 -6;0 2 -1 2;1 4 -7 6];b=[8;9;-5;0];
- x=inv(A)*b //Решение системы
//Результаты работы файла-сценария:
- --> x =
- 3.
- - 4.
- - 1.
- 1.
Метод Гаусса
Решение системы линейных уравнений при помощи метода Гаусса основывается на том, что от заданной системы, переходят к эквивалентной системе, которая решается проще, чем исходная система.
Метод Гаусса состоит из двух этапов. Первый этап это прямой ход, в результате которого расширенная матрица6 системы путем элементарных преобразований (перестановка уравнений системы, умножение уравнений на число отличное от нуля и сложение уравнений) приводится к ступенчатому виду. На втором этапе (обратный ход) ступенчатую матрицу преобразовывают так, чтобы в первых n столбцах получилась единичная матрица. Последний, n+1 столбец этой матрицы содержит решение системы линейных уравнений. Далее приведен текст файла-сценария и результаты его работы:
- //Матрица и вектор свободных коэффициентов системы:
- A=[2 -1 1;3 2 -5;1 3 -2]; b=[0;1;4];
- //Приведение расширенной матрицы к треугольному виду:
- C=rref([A b]);
- //Определение размерности расширенной матрицы:
- [n,m]=size(C); //m- номер последнего столбца матрицы С
- //Выделение последнего столбца из матрицы С:
- x=C(:,m) //x - решение системы
//Результаты работы программы:
- --> x =
- 0.4642857
- 1.6785714
- 0.75
Использование Simulink
Еще одним способом задания систем в виде передаточных функций является использование пакета Simulink, входящего в состав MatLab.
Для представления передаточной функции в Simulink используется блок Transfer Fcn. Блок передаточной характеристики Transfer Fcn задает передаточную функцию в виде отношения полиномов
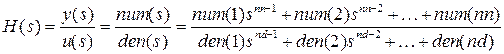 , (18)
, (18)
где nn и nd – порядок числителя и знаменателя передаточной функции, порядок числителя не должен превышать порядок знаменателя, num – вектор или матрица коэффициентов числителя, den – вектор коэффициентов знаменателя. Параметры блока Transfer Fcn:
– Numerator – вектор или матрица коэффициентов полинома числителя.
– Denominator – вектор коэффициентов полинома знаменателя.
– Absolute tolerance – абсолютная погрешность.
Исследование переходных характеристик осуществляется путем подачи на вход блока, представляющего передаточную функцию (блок Transfer Fcn), единичного ступенчатого сигнала (блоки Constant или Step). Входной сигнал блока должен быть скалярным. Чтобы получить переходный процесс, необходимо поместить на схему блок Scope и соединить его вход с выходом блока, переходный процесс которого необходимо получить. На рис. 6. показан пример моделирования колебательного звена с помощью блока Transfer Fcn (схема в Simulink и переходные процессы, полученные в блоке Scope). Начальные условия при использовании блока Transfer Fcn полагаются нулевыми.
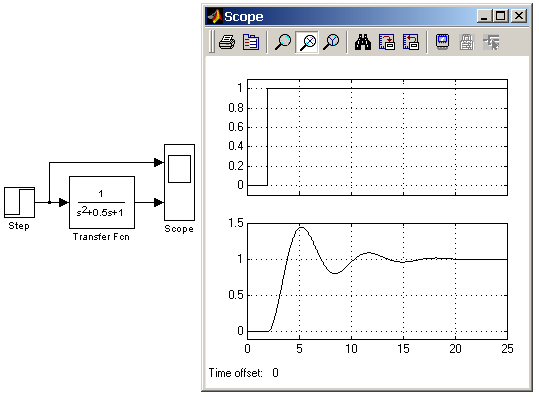
Рис. 6. Пример моделирования колебательного звена с помощью Simulink
Использование script-языка
При использовании script-языка SciLab для представления линейных систем используется функция syslin.
Синтаксис:
sl = syslin(dom, N, D)
sl = syslin(dom, H)
Параметры функции syslin:
dom – символьная переменная, которая может принимать два значения: 'c' или 'd'. dom определяет временной домен системы и может принимать следующие значения: dom='c' для систем непрерывных во времени; dom='d' для дискретно-временных систем;
N, D – полиномиальные матрицы;
H – рациональная матрица;
Выражение s = poly(0,'s') задаёт полином, соответствующий оператору Лапласа; переменная s может быть использована в дальнейшем. Наряду с таким заданием можно использовать и константу %s.
Далее приведены альтернативные способы задания двух ПФ 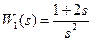 и
и 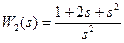 .
.
Пример 1:
s = poly(0, 's');
H1 =(1+2*s)/s^2
W1 = syslin('c', H1)
H2 = (1+2*s+s^2)/s^2
W2 = syslin('c', H2)
Пример 2:
s = poly(0, 's');
W1 = syslin('c', 1+2*s, s^2)
W2 = syslin('c', 1+2*s+s^2, s^2)
Пример 3:
W1 = syslin('c', 1+2*%s, %s^2)
W2 = syslin('c', 1+2*%s+%s^2, %s^2)
Для исследования временных характеристик используется функция csim, предназначенная для моделирования линейной системы
[y [,x]] = csim(u, t, sl),
где u – функция управления, принимает значения ‘step’ или ‘impulse’ в зависимости от вызываемой временной характеристики;
t – действительный вектор, характеризующий время; t(1) – начальное время x0=x(t(1));
sl – передаточная функция, представленная функцией syslin.
Далее рассмотрим в качестве примера моделирование апериодических звеньев первого порядка с различными значениями постоянных времени. Результат моделирования в виде переходных характеристик приведен на рис. 7.
Пример:
// построение переходных характеристик
// апериодического звена 1-го порядка
K = 1; // коэффициент усиления
T1 = 0.1; // постоянные времени
T2 = 0.5;
T3 = 1;
W1 = syslin('c', K/(T1*%s + 1));// задать ПФ
W2 = syslin('c', K/(T2*%s + 1));
W3 = syslin('c', K/(T3*%s + 1));
t = 0:0.05:5; // временной интервал
h1 = csim('step', t, W1); // моделирование подачи
h2 = csim('step', t, W2); // на вход ПФ
h3 = csim('step', t, W3); // ступенчатого воздействия
// построение графиков
plot(t, h1, 'r', t, h2, 'g', t, h3, 'b');
xgrid(2); // установка сетки на графике
// установка подписей графика и осей
xtitle('h(t)', 'time, c', 'h(t)');
legend('T=0.1', 'T=0.5', 'T=1'); // подпись легенды
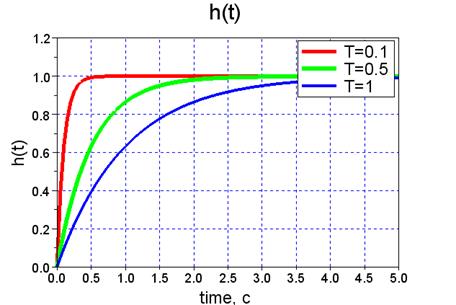
Рис. 7. Переходные характеристики апериодических звеньев в SciLab
Рекомендации по моделированию дифференцирующего
Таблица 6
Варианты заданий
| № в-та | Название звена | Значения параметров |
| Усилительное Интегрирующее | k = 1; 2; 5 | |
| Апрериодическое 1-го порядка Изодромное Интегрирующее с замедлением | 1) k = 1= const, T = 0,1; 0,5; 1 2) T = 0,5 =const, k = 0,5; 1; 5 | |
| Колебательное | 1) k = 1=const, T = 0.1= const, 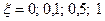 2) 2)  =const, k = 1=const, T = 0,1; 0,5; 1 3) =const, k = 1=const, T = 0,1; 0,5; 1 3) 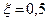 =const, T = 0,5 = const, k = 0,5; 1; 5 =const, T = 0,5 = const, k = 0,5; 1; 5 | |
| Усилительное, Интегрирующее | k = 0,5; 1; 2 | |
| Апериодическое 1-го порядка, Консервативное, Дифференцирующее с замедлением | 1) k = 2 =const, T = 0,1; 0,5; 1 2) T = 0,75=const, k = 0,5; 1; 5 |
Продолжение табл. 6
| № в-та | Название звена | Значения параметров |
| Колебательное | 1) k = 1=const, T = 0,25 = const, 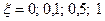 2) 2) 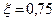 =const, k = 1= const, T = 0,1; 0,5; 1 3) =const, k = 1= const, T = 0,1; 0,5; 1 3) 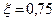 = const, T = 0.5=const, k = 0.5; 1; 5 = const, T = 0.5=const, k = 0.5; 1; 5 | |
| Усилительное Интегрирующее | k = 0,1; 0,2; 0,5 | |
| Апериодическое 1-го порядка Консервативное Дифференцирующее с замедлением | 1) k = 1= const, T = 0,1; 0,5; 0,75 2) T = 0,75 = const, k = 0,5; 1; 5 | |
| Колебательное | 1) k = 1=const, T = 0,1 = const, 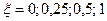 2) 2)  = const, k = 1 = const, T = 0,1; 0,5; 0,75 3) = const, k = 1 = const, T = 0,1; 0,5; 0,75 3)  = const, T = 0,5 = const, k = 0,5; 1; 5 = const, T = 0,5 = const, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 0,5; 1; 2 | |
| Апериодическое 1-го порядка Консервативное Дифференцирующее с замедлением | 1) k = 1=const, T = 0,1; 0,5; 1 2) T = 0,5 =const, k = 0,5; 1; 2 | |
| Колебательное | 1) k = 0,75 = const, T = 0,25 = = const, 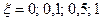 2) 2)  = const, k = 2 = const, T= 0,1; 0,5; 1 3) = const, k = 2 = const, T= 0,1; 0,5; 1 3)  = const, T = 0,75 = const, k = 0,5; 1; 5 = const, T = 0,75 = const, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 1; 2; 5 | |
| Апериодическое 1-го порядка Изодромное Интегрирующее с замедлением, | 1) k = 1= const, T = 0,1; 0,5; 1 2) T = 0,5 =const, k = 0.5; 1; 5 | |
| Колебательное | 1) k = 1=const, T = 0,25 = const, 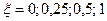 2) 2) 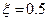 = const, k = 1 = const, T= 0,1; 0,5; 1 3) = const, k = 1 = const, T= 0,1; 0,5; 1 3)  = const, T = 0,5 = const, k = 0,5; 1; 2 = const, T = 0,5 = const, k = 0,5; 1; 2 |
Продолжение табл. 6
| № в-та | Название звена | Значения параметров |
| Усилительное Интегрирующее | k = 0,1; 0,2; 0,5 | |
| Апериодическое 1-го порядка Форсирующее 1-го порядка Изодромное | 1) k = 1=const, T = 0,1; 0,5; 1 2) T = 0,5 =const, k = 0,5; 1; 5 | |
| Колебательное Форсирующее 2-го порядка | 1) k = 1= const, T = 0,1= const, 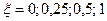 2) 2) 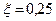 = const, k = 1 = const, T = 0,1; 0,5; 1 3) = const, k = 1 = const, T = 0,1; 0,5; 1 3) 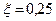 = const, T= 0,5 = const, k = 0,5; 1; 5 = const, T= 0,5 = const, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 0,1; 0,25; 0.5 | |
| Апериодическое 1-го порядка Консервативное Дифференцирующее с замедлением | 1) k = 2=const, T = 0,1; 0,5; 1 2) T = 1=const, k = 0,5; 1; 2 | |
| Колебательное | 1) k = 1=const, T = 0,1=const, 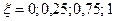 2) 2)  =const, k = 1=const, T = 0,1; 0,5; 0,75 3) =const, k = 1=const, T = 0,1; 0,5; 0,75 3)  =const, T = 0,5=const, k = 0,5; 1; 2 =const, T = 0,5=const, k = 0,5; 1; 2 | |
| Усилительное Интегрирующее Дифференцирующее | k = 0,25; 0,5; 1 | |
| Апериодическое 1-го порядка Дифференцирующее с замедлением | 1) k = 1=const, T = 0,1=const; 0,5; 0,75; 1 2) T = 0,5=const, k = 0,5; 1; 5 | |
| Колебательное | 1) k = 1=const, T = 0,5=const, 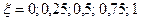 2) 2) 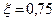 =const, k = 1=const, T = 0,1; 0,5; 1 3) =const, k = 1=const, T = 0,1; 0,5; 1 3) 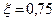 =const, T = 0,5 = const, k = 0,5; 1; 5 =const, T = 0,5 = const, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 1; 1,5; 2 |
Продолжение табл. 6
| № в-та | Название звена | Значения параметров |
| Апериодическое 1-го порядка Консервативное Дифференцирующее с замедлением | 1) k = 0,75 = const, T= 0,1; 0,5; 1 2) T = 0,75 =const, k = 0,5; 1; 5 | |
| Колебательное | 1) k = 1= const, T = 0,25, 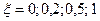 2) 2) 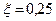 = const, k = 1= const, T = 0,1; 0,5; 1 3) = const, k = 1= const, T = 0,1; 0,5; 1 3) 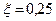 = const, T = 0,5, k = 0,5; 1; 5 = const, T = 0,5, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 0,25; 0,5; 1 | |
| Апериодическое 1-го порядка Консервативное Изодромное | 1) k = 1= const, T = 0,1; 0,5; 0,75; 1 2) T = 0,5=const, k = 0,5; 1; 2; 5 | |
| Колебательное | 1) k = 1,5= const, T = 0,25 = const, 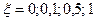 2) 2) 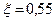 = const, k = 1= const, T = 0,1; 0,5; 1 3) = const, k = 1= const, T = 0,1; 0,5; 1 3) 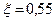 = const, T = 0,5 = const, k = 0,5; 1; 5 = const, T = 0,5 = const, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 1; 2; 5 | |
| Апериодическое 1-го порядка Изодромное Дифференцирующее с замедлением | 1) k = 1= const, T = 0,1; 0,5; 1 2) T = 0,5= const, k = 0,5; 1; 5 | |
| Колебательное | 1) k = 1= const, T = 0,25 = const, 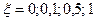 2) 2)  = const, k = 1= const, T = 0,25; 0,5; 1 3) = const, k = 1= const, T = 0,25; 0,5; 1 3)  =const, T = 0,75 = const, k = 0,5; 1; 5 =const, T = 0,75 = const, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 0,1; 0,25; 0,5 | |
| Апериодическое 1-го порядка Консервативное Форсирующее 1-го порядка | 1) k = 1= const, T = 0,1; 0,5; 1 2) T = 0,5 = const, k = 0,5; 1; 5 |
Окончание табл. 6
| № в-та | Название звена | Значения параметров |
| Колебательное | 1) k = 1,5 = const, T = 0,1=const, 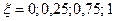 2) 2)  =const, k = 1,5 = const, T = 0,1; 0,5; 0,75 3) =const, k = 1,5 = const, T = 0,1; 0,5; 0,75 3)  =const, T = 0,25 = const, k = 0,5; 1; 2 =const, T = 0,25 = const, k = 0,5; 1; 2 | |
| Усилительное Интегрирующее | k = 0,5; 1; 2 | |
| Апериодическое 1-го порядка Консервативное Дифференцирующее с замедлением | 1) k = 1,25 = const, T = 0,25; 0,5; 1 2) T = 0,75 = const, k = 0,5; 1; 2 | |
| Колебательное | 1) k = 1= const, T = 0,25= const, 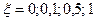 2) 2) 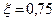 = const, k = 1, T = 0,1; 0,5; 1 3) = const, k = 1, T = 0,1; 0,5; 1 3) 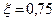 = const, T = 0,5= const, k = 0,5; 1; 5 = const, T = 0,5= const, k = 0,5; 1; 5 | |
| Усилительное Интегрирующее | k = 0,25; 0,75; 1 | |
| Апериодическое 1-го порядка Консервативное Форсирующее 1-го порядка Дифференцирующее с замедлением | 1) k = 1,5 = const, T = 0,1; 0,5; 1 2) T = 0,55 = const, k = 0,5; 1; 2 | |
| Колебательное | 1) k = 1= const, T = 0,25= const, 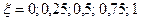 2) 2) 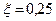 = const, k = 1= const, T = 0,1; 0,5; 1 3) = const, k = 1= const, T = 0,1; 0,5; 1 3) 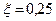 = const, T = 0,5= const, k = 0,5; 1; 2 = const, T = 0,5= const, k = 0,5; 1; 2 |
Варианты заданий
Задание 1. Стабилизация скорости вращения ДПТ

Рис. 57. Структурная схема стабилизации скорости вращения ДПТ НВ
Таблица 15
Передаточные функции регуляторов
| Регулятор | П | И | Пи |
ПФ регулятора  | 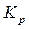 | 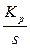 | 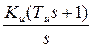 |
Устройство усиления имеет передаточную функцию 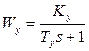 .
.
Таблица 16
Передаточные функции двигателя
| ПФ | ||
| ПФ ДПТНВ по скорости |  | 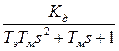 |
Таблица 17
Список вариантов заданий
| № | Регулятор |  | 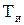 |  | 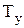 | ПФ ДПТНВ |  |  |  |
| П | 0,2 | 0,81 | 0,15 | 0,03 | |||||
| И | 0,5 | 0,03 | 0,73 | 0,04 | |||||
| Пи | 0,5 | 0,04 | 0,9 | 0,02 | |||||
| П | 0,05 | 0,75 | 0,12 | 0,02 | |||||
| И | 0,04 | 0,85 | 0,02 | ||||||
| Пи | 0,5 | 0,05 | 0,72 | 0,03 |
Задание 2. Следящая система
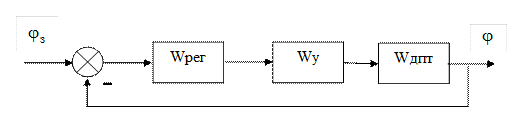
Рис. 58. Структурная схема следящей системы стабилизации положения ДПТ НВ
Таблица 18
Передаточные функции регуляторов
| Регулятор | П | И | Пи |
ПФ регулятора  | 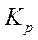 |  |  |
Устройство усиления имеет передаточную функцию  .
.
Таблица 19
Передаточные функции ДПТ по положению
| ПФ | ||
| ПФ ДПТНВ по положению |  |  |
Таблица 20
Список вариантов заданий
| № | Регулятор |  | 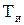 |  | ПФ ДПТНВ |  |  |  |
| П | 0,83 | 0,16 | 0,03 | |||||
| И | 0,74 | 0,03 | ||||||
| Пи | 0,1 | 0,81 | 0,03 | |||||
| П | 0,84 | 0,1 | 0,02 | |||||
| И | 0,8 | 0,02 | ||||||
| Пи | 0,5 | 0,85 | 0,03 |
Краткие сведения о средах моделирования Matlab и Scilab
Matlab и Scilab - это популярные системы компьютерной математики, которые предназначены для выполнения инженерных и научных вычислений, таких как:
· простейшие расчеты по формулам;
· решение нелинейных уравнений и систем;
· решение задач линейной алгебры;
· решение задач оптимизации;
· дифференцирование и интегрирование;
· задачи обработки экспериментальных данных;
· решение обыкновенных дифференциальных уравнений и систем;
· моделирование непрерывных и дискретных систем.
Кроме того, пакеты предоставляют широкие возможности по созданию и редактированию различных видов графиков и поверхностей.
Работа в Matlab и Scilab
