Раздел 4. Дискретные случайные величины.

Пусть производится некоторое испытание, результатом которого является одно из несовместных случайных событий 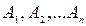(число событий или конечно или счетно, то есть события можно пронумеровать). Каждому исходу 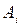поставлено в соответствие некоторое действительное число 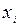, то есть на множестве случайных событий задана действительная функция Х со значениями 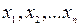. Эта функция Х называется дискретной случайной величиной (термин «дискретная» используется потому, что значения случайной величины – это отдельные числа, в отличии от непрерывных функций). Поскольку значения случайной величины изменяются в зависимости от случайных событий, то основной интерес представляют вероятности, с которыми случайная величина принимает различные числовые значения. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может иметь различные формы. Для дискретной случайной величины законом распределения является совокупность пар чисел ( 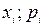), где 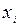– возможные значения случайной величины, а 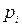– вероятности, с которыми она принимает эти значения: 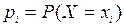. При этом .

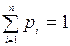Пары 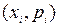можно рассматривать, как точки в некоторой системе координат. Соединив эти точки отрезками прямых, мы получим графическое изображение закона распределения – многоугольник распределения. Чаще всего закон распределения дискретной случайной величины записывается в виде таблицы, в которую внесены пары .

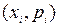X				…		…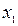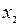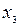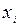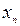
p				…		…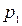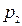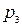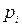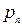

Пример. Монета подброшена два раза. Составить закон распределения числа выпадения «гербов» в данном испытании.

Решение. Случайная величина Х – число выпадений «герба» в данном испытании. Очевидно, что Х может принимать одно из трех значений: 0, 1, 2. Вероятность появления «герба» при одном подбрасывании монеты равна р=0,5, а выпадения «решки» q = 1 – p = 0,5. Вероятности, с которыми случайная величина принимает перечисленные значения, найдем по формуле Бернулли: .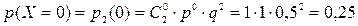

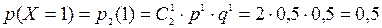
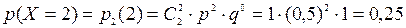
Закон распределения случайной величины Х запишем в виде таблицы распределения

Х
Р	0,25	0,5	0,25

Контроль: .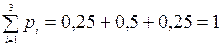

Некоторые законы распределения дискретных случайных величин, часто встречающиеся при решении различных задач, получили специальные названия: геометрическое распределение, гипергеометрическое распределение, биномиальное распределение, распределение Пуассона и другие.

Закон распределения дискретной случайной величины может быть задан с помощью функции распределения F(x), которая равна вероятности того, что случайная величина Х будет принимать значения на промежутке (-¥,х): F(x) = P(X<x).

Функция F(х) определена на всей действительной оси и обладает следующими свойствами:

1) £ F(х) £ 1;

2) F(х) – неубывающая функция;

3) F(-¥) = 0, F(+¥) = 1;

4) F(b) – F(a) = P(a £ X < b) – вероятность того, что случайная величина Х примет значения на промежутке [a,b).

График функции F(x) для дискретной случайной величины состоит из отрезков прямых и лучей, параллельных оси ОХ или совпадающих с ней.

Пример. Случайная величина Х задана таблицей распределения:

Х	- 1
Р	0,1	0,3	0,4	0,2

Составить функцию распределения F(x) случайной величины Х и построить ее график.

Решение. Если х£-1, то F(x)=P(X<x)=0;

если –1<x£2, то F(x)=P(X<x)=P(X=-1)=0;

если 2<х£3, то F(x)=P(X=-1)+P(X=2)=0,1+0,3=0,4;

если 3<x£5, то F(x)=P(X=-1)+P(X=2)+P(X=3)=0,1+0,3+0,4=0,8;

если х>5, то F(x)=P(X=-1)+P(X=2)+P(X=3)+ Р(Х=5)=1

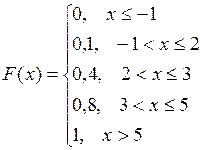
Построим график (рис. 3).

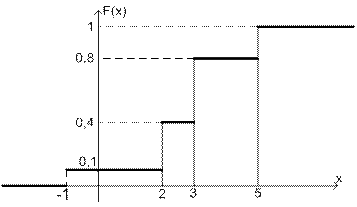
Рис. 1. График функции распределения.