Вероятность занятия серверов.

Найдем теперь вероятность занятия определенных, выбранных заранее серверов. Эта задача часто встречается при определении нагрузки на определенные выходы в коммутаторах каналов телефонных сетей. Будем исходить из того, что в результате применения модели Эрланга или Энгсета или Бернулли найдены вероятности занятия любых k серверов p_k .

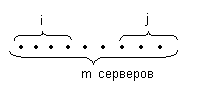
Зафиксируем определенные i серверов из m доступных. Предположим, что занятие серверов происходит равновероятно. Тогда если в системе с вероятностью 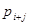занято точно i + j серверов, то вероятность занятия одной конкретной комбинации будет в число таких сочетаний раз меньше, т.е. .

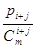Поскольку отмеченные i серверов могут быть заняты совместно с любыми другими j серверами в соответствующем числу сочетаний из m по j комбинациях, где j любое число от 0 до m-i , то можно получить формулу для вероятности занятия фиксированных i серверов в системе с M входами:

.

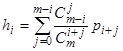Для модели Эрланга тогда получим:

.

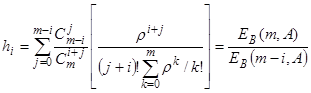Длямодели Энгсетаформула будет отличаться:

.

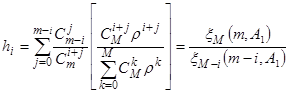Для системы с одинаковым числом входов и выходов (серверов) имеет место модель Бернулли и соответствующие вероятности занятия фиксированных серверов будут:

.

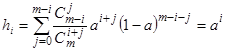Сравнительные характеристики моделей Эрланга и Энгсета

Мы будем сравнивать модели по получаемым с их помощью характеристик качества обслуживания (QoS).

Напомним сразу, что входной поток в модели Эрланга полагается Пуассоновским λ_n=λ а в модели Энгсета – примитивным λ_n=(M-n)l .

· Вероятность потерь по времени

Это вероятность занятости всех m серверов в системе при интенсивности нагрузки на входе А для модели Эрланга и максимальной нагрузке МА для модели Энгсета.

Модель Эрланга Модель Энгсета

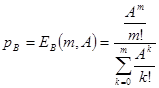
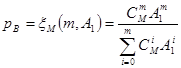
· Вероятность потерь вызова

Это отношение средних интенсивностей потоков потерянных и поступивших вызовов, т.е. вероятность того, что поступивший вызов застает систему в заблокированном состоянии.

Обозначим вероятности того, что вызов поступает при условии, когда система заблокирована (условная)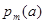

безусловную вероятность поступления вызова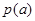

вероятность блокировки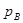

вероятность потери вызова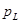

Из известных соотношений теории вероятностей имеем:

.

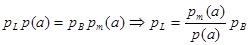Модель Эрланга.

Вероятность попадания вызова на заблокированную систему не зависит от состояния системы и в результате вероятность потери вызова совпадает с вероятностью блокировки по времени:

.

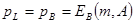Модель Энгсета.

Здесь для примитивного потока можно записать вероятности через интенсивности

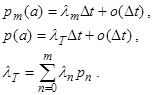
Последняя строка задает среднюю интенсивность вызовов по всем состояниям. Теперь вероятность потерь вызова может быть записана через интенсивности и далее вычислена через функцию Энгсета:

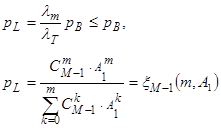
Как видно, .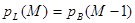

Если рассмотреть предел при стремлении числа входов к бесконечности, так что суммарная интенсивность потока останется постоянной, т.е. 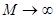, , 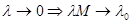то модель Энгсета превратится в модель Эрланга.

· Интенсивность обслуженной нагрузки