Cистема с конечным накопителем: M/M/1:N
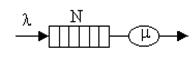
Рассмотрим СМО, для которой фиксировано максимальное число ожидающих заявок. Предположим, что в системе может находиться N заявок, включая находящуюся на обслуживании в сервере. Любое поступившее сверх этого числа требование получает отказ и немедленно покидает систему. В телефонии такие вызовы называют потерянными. Поступающие заявки образуют Пуассоновский поток, а обслуживание осуществляется одним сервером с показательным законом распределения времени обработки. Приспособим для описания такой системы модель процесса гибели-размножения.
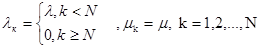
Эта система эргодична и диаграмма интенсивностей переходов может быть изображена так как на рис. 1.15.
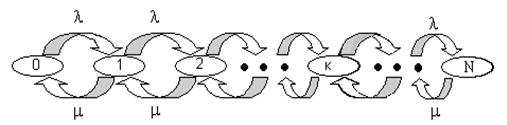
Рис. 1.15 Диаграмма интенсивностей переходов системы типа М/М/1:N.
Найдем распределение вероятностей в стационарном режиме непосредственно из общей формулы
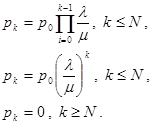
Найдем теперь начальную вероятность, следуя общей формуле:
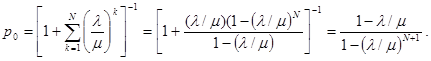
Таким образом, окончательная формула для стационарных вероятностей будет:
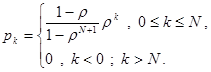
Проанализируем характеристики качества обслуживания (QoS) для такой системы. Важнейшей характеристикой будет являться вероятность блокировки – потери заявки. Очевидно, что это произойдет с вероятностью переполнения буфера, поэтому для расчета вероятности блокировки можно использовать формулу:
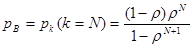 .
.
Например, для системы с коэффициентом использования 0.5 при размере буфера N=18 вероятность блокировки будет больше 10-6, а при размере N=19, меньше этого значения. Следовательно, для получения вероятности блокировки такой величины необходимо предусмотреть размер буфера не менее 19.
Средняя длина очереди в буфере может быть найдена как:
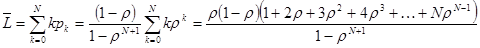 .
.
Соответственно задержка может быть найдена на основе формулы Литтла
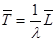 .
.
Определим пропускную способность системы как число заявок, обслуживаемых системой в одну секунду. Очевидно, что при вероятности блокировки PB пропускная способность может быть найдена как чистая интенсивность поступлений, то есть:
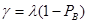 .
.
С точки зрения выхода системы пропускная способность может быть определена иначе. Если система всегда была бы непуста, то ее производительность равнялась бы величине обратной среднему времени обслуживания, то есть μ. Однако, поскольку часть времени система может простаивать, вероятность того, что в ней нет ни одной заявки отлична от нуля, реальная производительность может быть выражена как:
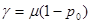 .
.
Подставив выражения для вероятности простоя сервера для системы с бесконечным размером буфера, получим:
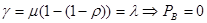 .
.
Для системы с конечным буфером получаем:
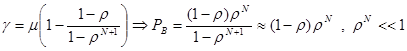 .
.
В качестве реального примера рассмотрим концентратор сети с коммутацией пакетов, который обрабатывает пакеты со средней длиной 1200 бит. При скорости передачи в канале 2400 бит/с средняя пропускная способность его составит μ=2 пакета/с. Если полный входной поток имеет интенсивность λ =1 пакет/с, то ρ =0.5 и можно рассчитать, что при размере буфера N =9 пакетов в среднем по 1200 бит, вероятность блокировки составит 0.001. Для того, чтобы получить вероятность блокировки 0.000 001 нужно предусмотреть буфер длиной не менее 19 пакетов по 1200 бит, т.е. около 2850 байт.
