Классификация систем массового обслуживания.

Используется трех -, четырех -, шести – компонентное символическое обозначение системы массового обслуживания, предложенное Кендаллом (Candall) и развитое в работах Г.П.Барашина.

A/b/c :d/e/f

a –распределение поступающего потока запросов.

b– закон распределения времени обслуживания.

Типовые условные обозначения:

М – экспоненциальное (Марковское) распределение,

D – детерминированное распределение,

E^k – эрланговское распределение k-го порядка,

HM^k – гиперэкспоненциальное,

HE^k – гиперэрланговское распределение порядка k,

GI – произвольное распределение независимых промежутков между заявками,

G – произвольное распределение длительностей обслуживания.

c –структура системы обслуживания (обычно число серверов).

d –дисциплина обслуживания (параметры после двоеточия иногда опускают).

Обычно используется сокращенное символическое обозначение, например FF вместо FIFO, LF, PR и т.п.

e –максимальное число запросов, воспринимаемое системой, может употребляться символ ¥.

f –максимальное число запросов к системе обслуживания.

В некоторых публикациях последними символами отражают качественные характеристики системы обслуживания. Некоторые общие результаты и основы математического аппарата, необходимого для анализа можно получить, рассматривая системы G/G/m.

Формула Литтла (Little).

Рассмотрим временную диаграмму работы системы массового обслуживания (рис. 1.8), отразив на ней последовательность поступления требований, помещение требований в очередь и обработки серверами системы.

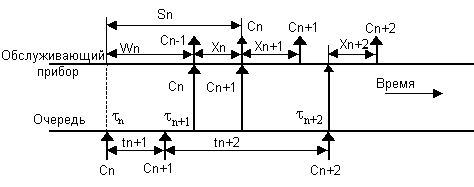
Рис. 1.8 Временная диаграмма работы системы массового обслуживания.

В общем случае ясно, что с увеличением числа требований растет время ожидания. Установим соотношение между средним числом требований в системе, интенсивностью потока и среднего времени пребывания в системе. Обозначим число поступающих в промежутке времени (0 , t) требований как функцию времени α(t).

Число исходящих из системы заявок (обслуженных) на этом интервале обозначим δ(t). На рисунке 1.9 показаны примеры функциональных зависимостей этих двух случайных процессов от времени.

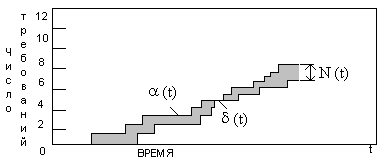
Рис. 1.9 Зависимость между средним числом требований в системе, интенсивностью потока и средним времени пребывания в системе.

Число требований, находящихся в системе в момент t будет равно:

.

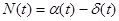Площадь между двумя рассматриваемыми кривыми от 0 до t - дает общее время, проведенное всеми заявками в системе за время t.

Обозначим эту накопленную величину γ(t) . Если интенсивность входного потока равна λ, а средняя интенсивность за время t: 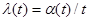,то время, проведенное одной заявкой в системе, усредненное по всем заявкам будет равно:

.

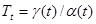Наконец, определим среднее число требований в системе в промежутке (0,t):

.

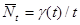Из последних трех уравнений следует, что: 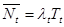, (где ).

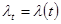Если в СМО существует стационарный режим, то при t→ ∞ , будут иметь место соотношения:

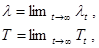
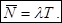
Последнее соотношение означает, что среднее число заявок в системе равно произведению интенсивности поступления требований в систему на среднее время пребывания в системе. При этом не накладывается никаких ограничений на распределения входного потока и времени обслуживания. Впервые доказательство этого факта дал Дж.Литтл и это соотношение носит название формула Литтла.

Интересно, что в качестве СМО можно рассмотреть только очередь из заявок в буфере. Тогда формула Литтла приобретает иной смысл - средняя длина очереди равна произведению интенсивности входного потока заявок на среднее время ожидания в очереди: .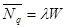

Если наоборот рассматривать СМО только как серверы, то формула Литтла дает:

,

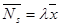где 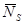– среднее число заявок в серверах, а 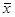– среднее время обработки в сервере.

В любом случае: .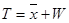

Одним из основных параметров, которые используются при описании СМО, является коэффициент использования (utilization factor). Это фундаментальный параметр, так как он определяется как отношение интенсивности входного потока к пропускной способности системы. Поскольку пропускная способность СМО содержащей m серверов может быть определена как: 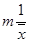, то коэффициент использования может быть определен как:

.

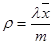Нетрудно видеть, что коэффициент использования равен в точности интенсивности нагрузки, если СМО с одним сервером и в m раз меньше для систем с m серверами. Величина коэффициента использования равна среднему значению от доли занятых серверов и .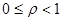

Если в СМО типа G/G/1 существует стационарный режим и можно определить вероятность того, что в некоторый случайный момент сервер будет свободный, то

.

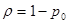Чтобы рассмотреть более тонкие результаты теории телетрафика нам понадобится ряд математических моделей.

Теперь перейдем к рассмотрению самой простой из задач анализа СМО – рассмотрим систему типа M/M/1.

1.3 Анализ систем массового обслуживания с марковскими потоками требований.

В этом разделе вы познакомитесь с методами расчета характеристик качества обслуживания QоS систем массового обслуживания, если они могут быть описаны моделью с марковским потоком требований на входе, т.е. интервалы времени между поступлениями соседних требований являются случайной величиной с экспоненциальным распределением.

Система М/M/1. Анализ.

Как было описано при классификации систем, это система с пуассоновским входным потоком заявок, экспоненциальным законом распределения времени обслуживания и одним сервером.

На рис. 1.10 приведена простейшая схема такой системы. Она содержит буфер, который может хранить очередь бесконечной длины, состояние которой может быть отождествлено с числом заявок, содержащихся в очереди в каждый момент времени.

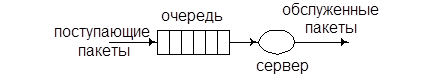
Рис. 1.10 СМО типа М/М/1.

Поскольку входной процесс ординарный, то в каждый момент времени к очереди может добавиться только одна заявка, поскольку сервер один, то в каждый момент времени может быть обслужена, то есть уйти из очереди только одна заявка. Таким образом, рассматриваемая СМО относится к процессу класса «гибели-размножения». Для анализа необходимо конкретизировать параметры системы. Распределение вероятностей входного потока и времени обслуживания позволяет полагать интенсивности вероятностей в модели постоянными.

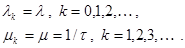
Здесь t – среднее время обслуживания в сервере.

На рис 1.11 приведена диаграмма интенсивностей переходов для рассматриваемой системы.

Рис. 1.11 Диаграмма интенсивности переходов для СМО типа М/М/1.

Полученное ранее общее решение позволяет сразу записать вероятность того, что в стационарном состоянии в очереди будет находиться k заявок

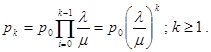
Найдем начальное значение вероятности, учитывая сходимость соответствующего ряда

.

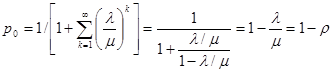Окончательно получаем формулу для вероятности длины очереди

.

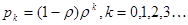На рис. 1.12 приведен график вероятностей того, что в очереди находится k заявок в установившемся режиме.

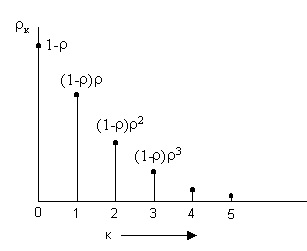
Рис. 1.12 Стационарные вероятности р_к для СМО типа М/М/1.

Теперь найдем наиболее интересные характеристики.

Важной характеристикой системы является средняя длина очереди. Зная вероятности каждого из возможных значений длины, найдем математическое ожидание:

.

График средней длины очереди заявок в системе в зависимости от значения коэффициента использования или нагрузки показан на рис. 1.13.

Найдем теперь дисперсию длины очереди: .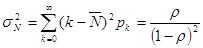

Для нахождения среднего значения времени пребывания в очереди воспользуемся формулой Литтла.

.

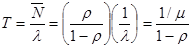На рис. 1.14 приведен график зависимости среднего времени пребывания в очереди в зависимости от коэффициента использования (нагрузки).

Рассматривая полученные результаты, нетрудно видеть, что при увеличении коэффициента использования, как длина очереди, так и время пребывания в ней неограниченно возрастают при приближении ρ к единице. Такой вид зависимости от коэффициента использования характерен для почти всех СМО.

Наконец найдем вероятность того, что в очереди будет находиться не менее чем k заявок и того, что в очереди менее k заявок.

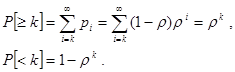
Итак, в ходе анализа простей шей системы М/М/1 нам удалось в аналитическом виде найти все практически интересные характеристики Q_oS системы.