Признак сходимости Даламбера.

Перед тем как сформулировать сам признак, рассмотрим важный вопрос:
Когда нужно применять признак сходимости Даламбера?

!!! Основные предпосылки для применения признака Даламбера следующие:

1) В общий член ряда («начинку» ряда) входит какое-нибудь число в степени, например, 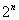, , 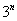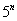и так далее. Причем, совершенно не важно, где эти функции располагается, в числителе или в знаменателе – важно, что они там присутствуют.

2) В общий член ряда входит факториал. Что такое факториал?





…


…

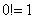
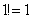
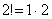
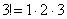
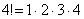
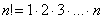
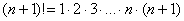
! При использовании признака Даламбера нам как раз придется расписывать факториал подробно. Как и в предыдущем пункте, факториал может располагаться вверху или внизу дроби.

3) Если в общем члене ряда есть «цепочка множителей», например, 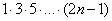. Этот случай встречается редко.

! Вместе со степенями или (и) факториалами в начинке ряда часто встречаются многочлены, это не меняет дела – нужно использовать признак Даламбера.

! Кроме того, в общем члене ряда может встретиться одновременно и степень и факториал; может встретиться два факториала, две степени, важно чтобы там находилось хоть что-то из рассмотренных пунктов – и это как раз предпосылка для использования признака Даламбера.

Признак Даламбера: Рассмотрим положительный числовой ряд 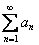. Если существует предел отношения последующего члена к предыдущему: 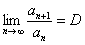, то:
а) При 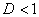ряд сходится. В частности, ряд сходится при .
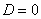б) При 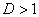ряд расходится. В частности, ряд расходится при .
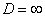в) При 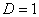признак не дает ответа. Нужно использовать другой признак. Чаще всего единица получается в том случае, когда признак Даламбера пытаются применить там, где нужно использовать предельный признак сравнения.

!!! Без понимания предела и умения раскрывать неопределенность 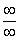дальше, к сожалению, не продвинуться.

Пример: Исследовать ряд на сходимость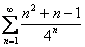
Решение: Мы видим, что в общем члене ряда у нас есть 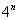, а это верная предпосылка того, что нужно использовать признак Даламбера.

Используем признак Даламбера:

Таким образом, исследуемый ряд сходится.

Радикальный признак Коши.

Признак сходимости Коши для положительных числовых рядов чем-то похож на только что рассмотренный признак Даламбера.

Радикальный признак Коши:Рассмотрим положительный числовой ряд 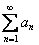. Если существует предел: 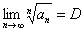, то:
а) При 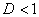ряд сходится. В частности, ряд сходится при .
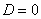б) При 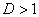ряд расходится. В частности, ряд расходится при .
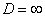в) При 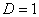признак не дает ответа. Нужно использовать другой признак.

! Интересно отметить, что если признак Коши не даёт нам ответа на вопрос о сходимости ряда, то признак Даламбера нам тоже не даст ответа. Но если признак Даламбера не даёт ответа, то признак Коши вполне может «сработать». То есть, признак Коши является в этом смысле более сильным признаком.

!!! Когда нужно использовать радикальный признак Коши? Радикальный признак Коши обычно использует в тех случаях, когда общий член ряда ПОЛНОСТЬЮ находится в степени, зависящей от «эн». Либо когда корень 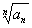«хорошо» извлекается из общего члена ряда. Есть еще экзотические случаи, но ими голову забивать не будем.

Пример: Исследовать ряд на сходимость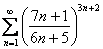

Решение: Мы видим, что общий член ряда полностью находится под степенью, зависящей от 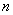, а значит, нужно использовать радикальный признак Коши:

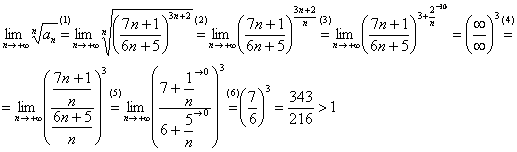
Таким образом, исследуемый ряд расходится.

Интегральный признак Коши.

Для того чтобы применять интегральный признак Коши необходимо более или менее уверенно уметь находить производные, интегралы, а также иметь навык вычисления несобственного интеграла первого рода.

Сформулирую своими словами (для простоты понимания).

Интегральный признак Коши: Рассмотрим положительный числовой ряд 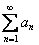. Данный ряд сходится или расходится вместе с соответствующим несобственным интегралом.

!!! Основной предпосылкой использования интегрального признака Коши является тот факт, что в общем члене ряда есть некоторая функция и её производная.

Пример: Исследовать ряд на сходимость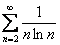

Решение: Из темы Производная вы наверняка запомнили простейшую табличную вещь: 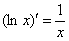, и у нас как раз такой канонический случай.

Как использовать интегральный признак? Сначала берем значок интеграла и переписываем со «счётчика» ряда верхний и нижний пределы: 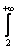. Затем под интегралом переписываем «начинку» ряда с буковкой «икс»: .

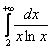Теперь нужно вычислить несобственный интеграл 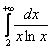. При этом возможно два случая:

1) Если выяснится, что интеграл 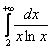сходится, то будет сходиться и наш ряд .

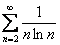2) Если выяснится, что интеграл 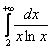расходится, то наш ряд 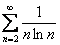тоже будет расходиться.

Используем интегральный признак:

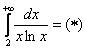
Подынтегральная функция непрерывна на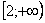

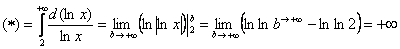
Таким образом, исследуемый ряд расходится вместе с соответствующим несобственным интегралом.

Пример: Исследовать сходимость ряда

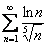
Решение: прежде всего, проверяем необходимый признак сходимости ряда. Это не формальность, а отличный шанс расправиться с примером «малой кровью».

Числовая последовательность 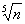более высокого порядка роста, чем 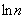, поэтому 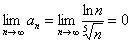, то есть необходимый признак сходимости выполнен, и ряд может, как сходиться, так и расходиться.

Таким образом, нужно использовать какой-либо признак. Но какой? Предельный признак сравнения явно не подходит, поскольку в общий член ряда затесался логарифм, признаки Даламбера и Коши тоже не приводят к результату. Если бы у нас был 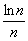, то худо-бедно можно было бы вывернуться через интегральный признак.

«Осмотр места происшествия» наводит на мысль о расходящемся ряде 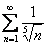(случай обобщенного гармонического ряда), но опять же возникает вопрос, как учесть логарифм в числителе?

Остаётся самый первый признак сравнения, основанный на неравенствах, который часто не принимается во внимание и пылится на дальней полке. Распишем ряд подробнее:

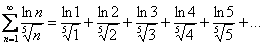
Напоминаю, что 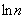– неограниченно растущая числовая последовательность:

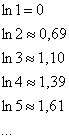
И, начиная с номера 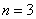, будет выполнено неравенство :

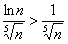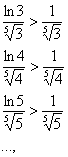
то есть, члены ряда 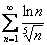будут ещё больше соответствующих членов расходящегося ряда .

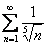В итоге, ряду 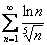ничего не остаётся, как тоже расходиться.

!!! Сходимость или расходимость числового ряда зависит от его «бесконечного хвоста» (остатка). В нашем случае мы можем не принимать во внимание тот факт, что неравенство 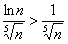неверно для первых двух номеров – это не оказывает влияния на сделанный вывод.

Чистовое оформление примера должно выглядеть примерно так:

Сравним данный ряд с расходящимся рядом .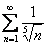
Для всех номеров, начиная с 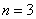, выполнено неравенство 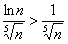, следовательно, по признаку сравнения исследуемый ряд расходится.

Знакочередующиеся ряды. Признак Лейбница. Примеры решений.

Что такое знакочередующийся ряд?Это понятно или почти понятно уже из самого названия. Сразу простейший пример.

Рассмотрим ряд 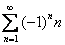и распишем его подробнее:

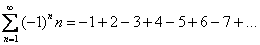
Знакочередование обеспечивает множитель 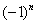: если 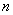чётное, то будет знак «плюс», если нечётное – знак «минус»

!!! В практических примерах знакочередование членов ряда может обеспечивать не только множитель 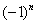, но и его родные братья: 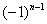, , 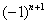, 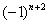…. Например:

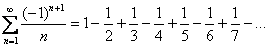
!!! Подводным камнем являются «обманки»: 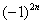, , 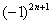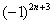и т.п. – такие множители не обеспечивают смену знака. Совершенно понятно, что при любом натуральном : , , .

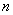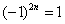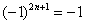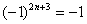Как исследовать знакочередующийся ряд на сходимость?Использовать признак Лейбница.

Признак Лейбница: Если в знакочередующемся ряде 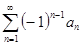выполняются два условия: 1) члены ряда монотонно убывают по абсолютной величине 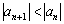. 2) предел общего члена по модулю равен нулю 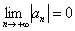, то ряд сходится, и модуль суммы этого ряда не превосходит модуля первого члена.

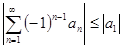
Краткая справка о модуле:

Что значит «по модулю»? Модуль, как мы помним со школы, «съедает» знак «минус». Вернемся к ряду 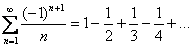. Мысленно сотрём ластиком все знаки и посмотрим на числа. Мы увидим, что каждый следующий член ряда меньше, чем предыдущий.

Теперь немного про монотонность.

Члены ряда строго монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю МЕНЬШЕ, чем предыдущий: 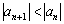. Для ряда 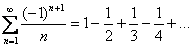выполнена строгая монотонность убывания, её можно расписать подробно:

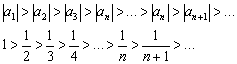
А можно сказать короче: каждый следующий член ряда по модулю меньше, чем предыдущий: .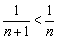

Члены ряда нестрого монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю НЕ БОЛЬШЕ предыдущего: 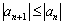. Рассмотрим ряд с факториалом: 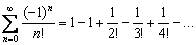Здесь имеет место нестрогая монотонность, так как первые два члена ряда одинаковы по модулю. То есть, каждый следующий член ряда по модулю не больше предыдущего: .

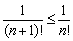!!! В условиях теоремы Лейбница должна выполняться монотонность убывания (неважно, строгая или нестрогая). При этом члены ряда могут даже некоторое время возрастать по модулю, но «хвост» ряда обязательно должен быть монотонно убывающим.

Пример: Исследовать ряд на сходимость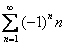

Решение: В общий член ряда входит множитель 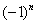, а значит, нужно использовать признак Лейбница

1) Проверка ряда на монотонное убывание.

1<2<3<…, т.е. n+1>n – первое условие не выполняется

2) 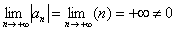– второе условие тоже не выполнено.

Вывод: ряд расходится.

Определение: Если ряд сходится по признаку Лейбница и ряд, составленный из модулей: 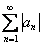тоже сходится, то говорят, что ряд сходится абсолютно.

Если ряд сходится по признаку Лейбница, а ряд, составленный из модулей: 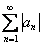расходится, то говорят, что ряд сходится условно.

Достаточный признак сходимости знакочередующегося ряда:Если ряд, составленный из модулей сходится, то сходится и данный ряд.

!!! Поэтому знакочередующейся сходящийся ряд необходимо исследовать на абсолютную или условную сходимость.

Пример: Исследовать ряд на условную или абсолютную сходимость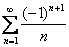

Решение: Используем признак Лейбница:

1) Каждый следующий член ряда по модулю меньше, чем предыдущий: 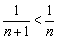– первое условие выполнено.

2) 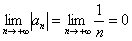– второе условие тоже выполнено.

Вывод: ряд сходится.

Проверим на условную или абсолютную сходимость.

Составим ряд из модулей – опять просто убираем множитель, который обеспечивает знакочередование:
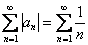– расходится (гармонический ряд).

Таким образом, наш ряд не является абсолютно сходящимся.
Исследуемый ряд 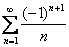сходится условно.

Пример: Исследовать ряд на условную или абсолютную сходимость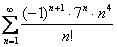

Решение: Используем признак Лейбница:
1) Попробуем записать несколько первых членов ряда:


…?!

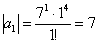
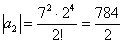
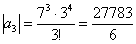2)

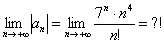
Дело в том, что не существует стандартных обыденных приемов для решения подобных пределов. Куда стремится такой предел? К нулю, к бесконечности? Здесь важно, ЧТО на бесконечности растёт быстрее – числитель или знаменатель.

Если числитель 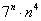при 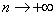растёт быстрее факториала, то 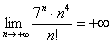. Если, на бесконечности факториал растёт быстрее числителя, то он, наоборот – «утянет» предел на ноль: 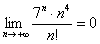. А может быть этот предел равен какому-нибудь отличному от нуля числу?

Записали несколько первых членов ряда:

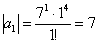
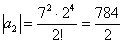
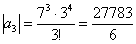
Создается стойкое впечатление, что 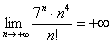, но где гарантия, что при очень больших «эн» факториал не «обгонит» числитель и не утащит предел на ноль?

Обратимся к теории математического анализа:

!!! Справка

– Факториал растёт быстрее, чем любая показательная последовательность, иными словам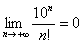и: или 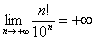. Да хоть миллион в степени «эн», это не меняет дела. То есть, факториал более высокого порядка роста, чем любая показательная последовательность.

– Факториал растёт быстрее, чем любая степенная последовательность или многочлен, иными словам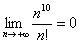и: или 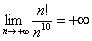. Вместо 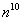можно подставить какой-нибудь многочлен тысячной степени, это опять же не изменит ситуацию – рано или поздно факториал всё равно «перегонит» и такой страшный многочлен. Факториал более высокого порядка роста, чем любая степенная последовательность.

– Факториал растёт быстрее, чем произведение любого количества показательных и степенных последовательностей (наш случай).

– Любая показательная последовательность растёт быстрее, чем любая степенная последовательность, например: 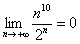, 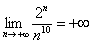. Показательная последовательность более высокого порядка роста, чем любая степенная последовательность. Аналогично факториалу, показательная последовательность «перетягивает» произведение любого количества любых степенных последовательностей или многочленов: .

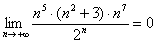– А есть ли что-нибудь «сильнее» факториала? Есть! Степенно-показательная последовательность («эн» в степени «эн») растёт быстрее факториала. На практике встречается редко, но информация лишней не будет.

Конец справки

Таким образом, второй пункт исследования можно записать так:
2) 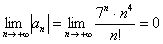, так как 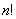более высокого порядка роста, чем .
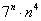Члены ряда убывают по модулю, начиная с некоторого номера 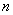, при этом, каждый следующий член ряда по модулю меньше, чем предыдущий, таким образом, убывание монотонно.

Вывод: ряд сходится.

!!! Вот здесь как раз тот любопытный случай, когда члены ряда сначала растут по модулю, из-за чего у нас сложилось ошибочное первоначальное мнение о пределе. Но, начиная с некоторого номера «эн», факториал обгоняет числитель, и «хвост» ряда становится монотонно убывающим, что является принципиально важным для выполнения условия теоремы Лейбница. Чему конкретно равно данное «эн», выяснить достаточно трудно.

Исследуем ряд на абсолютную или условную сходимость:

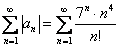
А тут уже работает признак Даламбера:

Используем признак Даламбера:

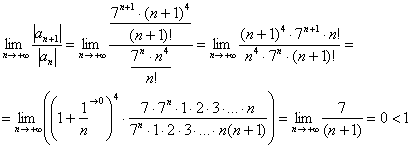
Таким образом, ряд 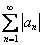сходится.

Исследуемый ряд сходится абсолютно.

Разобранный пример можно решить другим способом (используем достаточный признак сходимости знакочередующегося ряда).

Достаточный признак сходимости знакочередующегося ряда:Если ряд составленный из абсолютных величин членов данного ряда, сходится, то сходится и данный ряд.

Второй способ:

Исследовать ряд на условную или абсолютную сходимость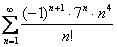

Решение: Исследуем ряд на абсолютную сходимость:

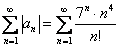
Используем признак Даламбера:

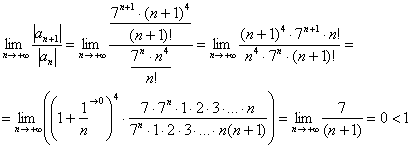
Таким образом, ряд 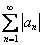сходится.
Исходя из достаточного признака сходимости знакочередующегося ряда, сходится и сам ряд .

Вывод: Исследуемый ряд сходится абсолютно.

Для вычисления суммы ряда с заданной точностьюбудем использовать следующую теорему:

Пусть знакочередующийся ряд 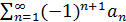удовлетворяет условиям признака Лейбница и пусть 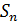– его n-ая частичная сумма. Тогда ряд сходится и погрешность 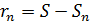при приближенном вычислении его суммы S по абсолютной величине не превосходит модуля первого отброшенного члена:

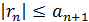
Функциональные ряды. Степенные ряды.
Область сходимости ряда.

Для успешного освоения темы нужно хорошо разбираться в обычных числовых рядах.