Системы с конечным временем наблюдения

Рассмотрим нестационарную линейную систему

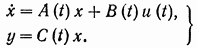(13.1)

Здесь x — n-мерный вектор состояния системы, u(t) - r-мерный вектор, представляющий собой сигнал на входе системы, y(t) m-мерный вектор, определяющий собой выход системы, A(t) – n X n-матрица,
B(t) — n X r-матрица, C(t) — m X n-матрица . Предполагается, что система (1) вполне наблюдаема.

Входной сигнал u(t) есть векторный случайный гауссов процесс типа белого шума с нулевым средним значением

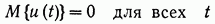(13.2)

и корреляционной матрицей

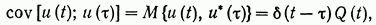(13.3)

где — δ(t) дельта-функция Дирака, Q(t) —симметрическая, неотрицательно-определенная r X r - матрица.

Дельта-функция – единичная импульс функция –обобщенная функция, которая позволяет записать точечное воздействие.

t

Х

Пусть t˳ начальный момент времени (t₀ > - ∞) , а вектор x(t₀) - начальное состояние системы. Предполагается, что x(t₀) гауссова векторная случайная величина, не зависящая от u(t) с известным средним значением

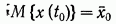(13.4)

и известной корреляционной матрицей

(13.5)

В сделанных выше предположениях x(t) и y(t) являются гауссовыми случайными процессами.

Предположим, что наблюдение вектора y(t) происходит при наличии помех типа гауссова белого шума, и поэтому наблюдаемый сигнал имеет вид

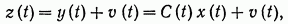(13.6)

где υ(t) — гауссов белый шум с нулевым средним значением

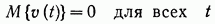(13.7)

и корреляционной матрицей

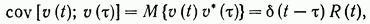(13.8)

где R(t) — симметрическая, положительно-определенная m X m -матрица. Кроме того, предполагается, что υ(t), u(t) и x(t˳) некоррелированы.

Пусть теперь требуется получить оценку ẋ(t) состояния x(t) системы (1) по доступной измерению на отрезке времени [t₀ , T] вектор-функции z(t).
(Вектор-функции x(t) и y(t) непосредственно недоступны измерению.) Систему, которая будет определять вектор ẋ(t) , назовем фильтром. Здесь мы ограничимся фильтрами, представляющими собой нестационарные линейные системы вида

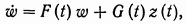(13.9)

где ω(t) - n-мерный вектор, F(t) – n X n -матрица, G(t) n X m -матрица.
Вектор функция ω(t) принимается в качестве оценки ẋ(t) состояния x(t) исходной системы (1)

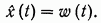(13.10)

В соответствии с (10) ошибка оценки e(t) = x(t) - ẋ(t) будет иметь следующий вид:

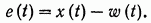(13.11)

Вектор-функция e(t) может быть названа ошибкой фильтра.

К фильтру (9) предъявим следующие требования: вектор-функция ω(t) должна представлять собой несмещенную оценку x(t) и при этом должна минимизировать дисперсию ошибки e(t) (точнее, минимизировать некоторый функционал, зависящий от корреляционной матрицы векторного случайного процесса e(t)).
Из этих требований и надлежит выбрать матрицы F(t) и G(t) и начальное состояние фильтра ω(t₀).

Это точная оценка, математическое ожидание которой равна оцениваемому параметру

Фильтр, обеспечивающий несмещенность оценки x(t) будет описываться дифференциальным уравнением

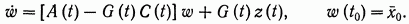(13.12)

Рассмотрим функционал

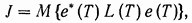(13.13)

где T — некоторый фиксированный момент времени, L(T) — симметрическая, положительно-определенная n X n-матрица. Так как скалярное произведение a*b двух n-мерных векторов а и b равно следу n X n -матрицы ba*, то есть сумме элементов, расположенных на ее главной диагонали

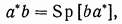(13.14)

Оптимальный фильтр представляет собой систему с обратной связью, сигнал на входе которой состоит из зависящей от рассогласования функции С(t) e(t) и аддитивной помехи в виде белого шума υ(t).