Метод А. Н. Колмогорова и Н. Винера. Стационарные случайные процессы
Рассмотрим одномерную линейную управляемую систему, на вход которой поступает сигнал
 (12.1)
(12.1)
где  - полезный сигнал, а
- полезный сигнал, а  - помеха. Будем считать, что
- помеха. Будем считать, что  и
и  - стационарные случайные процессы с нулевыми средними значениями. Назначением системы является возможно более точное преобразование (в частном случае — воспроизведение) полезного сигнала
- стационарные случайные процессы с нулевыми средними значениями. Назначением системы является возможно более точное преобразование (в частном случае — воспроизведение) полезного сигнала 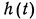 .
.
Передаточную функцию системы обозначим через 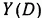 , а ее функцию веса через
, а ее функцию веса через  .
.
Сигнал на выходе системы (в предположении, что начальный момент времени 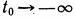 будет иметь следующий вид:
будет иметь следующий вид:
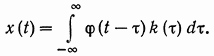 (12.2)
(12.2)
Пусть система предназначена для прогноза полезного входного сигнала. Для осуществления прогноза потребуем, чтобы сигнал  на выходе системы в момент времени t представлял собой наилучшее (в смысле минимума дисперсии ошибки) приближение к
на выходе системы в момент времени t представлял собой наилучшее (в смысле минимума дисперсии ошибки) приближение к  , где
, где 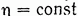 . При
. При 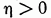 имеем задачу прогноза. При
имеем задачу прогноза. При  рассматриваемая задача является задачей фильтрации входного сигнала.
рассматриваемая задача является задачей фильтрации входного сигнала.
Ошибка приближения сигнала  на выходе системы к
на выходе системы к 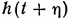 будет
будет
 (12.3)
(12.3)
или в соответствии с (2)
 (12.4)
(12.4)
Дисперсия ошибки приближения будет
 (12.5)
(12.5)
Будем искать теперь функцию веса  , которая доставляет минимум функционалу
, которая доставляет минимум функционалу 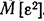 . Указанную функцию веса будем считать оптимальной функцией веса, а соответствующую ей систему оптимальной линейной системой.
. Указанную функцию веса будем считать оптимальной функцией веса, а соответствующую ей систему оптимальной линейной системой.
Найдем теперь необходимое условие, которому должна удовлетворять функция 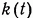 для того, чтобы она доставляла минимум функционалу
для того, чтобы она доставляла минимум функционалу
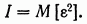 (12.6)
(12.6)
Для этого заменим  функцией
функцией 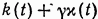 , где
, где 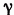 — некоторый произвольный параметр, не зависящий от t, а
— некоторый произвольный параметр, не зависящий от t, а  - произвольная функция, которая аналогично функции
- произвольная функция, которая аналогично функции  , удовлетворяет требованию
, удовлетворяет требованию
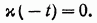
Необходимое условие минимума функционала (7) имеет вид
 (12.7)
(12.7)
И принимает вид
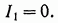 (12.8)
(12.8)
Нетрудно видеть, что условие является не только необходимым, но и достаточным условием минимума функционала 1.
Таким образом условие является необходимым и достаточным условием минимума дисперсии 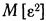 .
.
Так как условие (19) должно выполняться при любых функциях  то в соответствии с (17) условие минимума дисперсии
то в соответствии с (17) условие минимума дисперсии 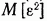 принимает вид
принимает вид
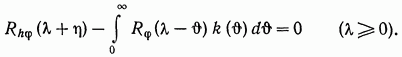 (12.8)
(12.8)
Таким образом, функция веса 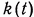 , удовлетворяющая интегральному уравнению (8), обеспечивает минимально возможное значение дисперсии ошибки
, удовлетворяющая интегральному уравнению (8), обеспечивает минимально возможное значение дисперсии ошибки 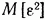 .
.
Интегральное уравнение (8) получено H. Винером [8]. Чтобы согласовать с обозначениями Винера, заменим в (8) переменную интеграцию Θ на Λ. Аргумент корреляционных функций 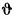 и
и 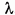 , который в (8) обозначен через
, который в (8) обозначен через  , заменим на
, заменим на 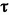 .
.
Х примет тогда вид
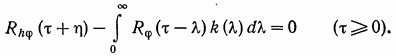 (12.9)
(12.9)
В задаче фильтрации, то есть при
 (12.10)
(12.10)
оптимальная функция веса 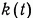 должна в соответствии с (9) удовлетворять интегральному уравнению
должна в соответствии с (9) удовлетворять интегральному уравнению
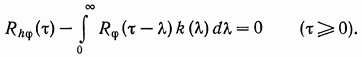 (12.11)
(12.11)
Многомерные случайные процессы. Оптимальные фильтры Кальмана — Бьюси.
