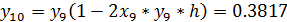Методы решения однородных дифференциальных уравнений

Министерство образования и науки РФ

ФГБОУ ВПО «Кубанский государственный технологический

Университет»

Кафедра электротехники и электрических машин

УТВЕРЖДАЮ
Заведующий кафедрой электротехники и электрических машин
к.т.н., доцент		ЯЯ.М. Кашин
____ _______ 2015 г.

Конспект лекций

По дисциплине «Численные методы расчета

Электрооборудования»

для студентов направления 13.04.02 «Электроэнергетика и электротехника»

Квалификация выпускника – магистр

Разработал:

к.т.н., доц. И.Н. Автайкин

Обсужден на заседании кафедры

электротехники и электрических машин

25 августа 2015 г. (протокол № 1)

Секретарь кафедры

к.т.н., доц. С.А. Попов

2015 г.

Лекция № 1 (2 часа)

По дисциплине «Численные методы расчета электрооборудования»

Тема № 4. Численное дифференцирование

Цели: 1. Формирование следующих компетенций:

ПК_Д-3 Способностью к освоению и применению современных средств анализа и моделирования работы электрооборудования

2. Формирование уровня обученности:

Знать: современных средств анализа и моделирования работы электрооборудования.

Уметь: применять современные методы решения математических задач с использованием компьютерной техники.

Владеть: современным математическим аппаратом позволяющим анализировать математические модели электрооборудования.

Материальное обеспечение:

Учебные вопросы

1. Метод Эйлера;

2. Усовершенствованный метод Эйлера;

3. Модифицированный метод Эйлера;

4. Метод Рунге-Кута.

Литература

1. Бахвалов Н.С., Жидков Н.П. Кобельков Г.М. Численные методы / Учебн. пособие- М.: Наука, 2011.- 631с.

2. Марчук Г.И. Методы вычислительной математики / Учебн. пособие- М.: Наука, 2011.- 535с.

Методы решения однородных дифференциальных уравнений.

Дифференциальным называется уравнение, содержащее один или несколько производных. В зависимости от количества не зависимых переменных, дифференциальные уравнения делятся на две категории.

1) Обыкновенные дифференциальные уравнения (ОДУ)

2) Дифференциальные уравнения в частных производных.

Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функции 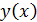. Их можно записать виде

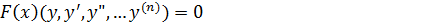(1)

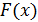независимая переменная

Наивысший порядок 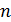, входящий в уравнение (1) называется порядком дифференциального уравнения.

Простейшим (линейным) ОДУ является уравнение (1) разрешенное относительно производной

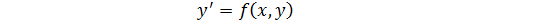(2)

Решением дифференциального уравнения (1) называется всякая функция, 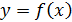которая после ее подстановки в уравнение обращает его в тождество.

Основная задача, связанная с линейной ОДУ известно как задача Каши: найти решение уравнения (2) в виде функции 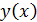удовлетворяющий начальному условию 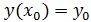(3)

Геометрически это означает, что требуется найти интегральную кривую, 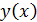проходящую через точку 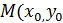) при выполнение равенства (2).

Численный с точки зрения задачи Каши означает: требуется построить таблицу значений функции 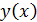удовлетворяющий уравнение (2) и начальное условие (3) на отрезке 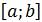с некоторым шагом 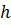. Обычно считается, что 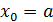то есть начальное условие задано в левом конце отрезка.

Метод Эйлера.

Простейшим из численных методов решения дифференциального уравнения является метод Эйлера. В его основе лежит идея графического построения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной форме или таблицы.

Пусть дано уравнение 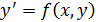с начальным условием 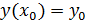то есть поставлена задача Каши. Решим вначале следующую задачу. Найти простейшим способом приближенное значение решения в некоторой точк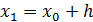е где 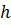-достаточно малый шаг. Уравнение (2) совместно с начальным условием (3) задают направление касательной искомой интегральной кривой в точке 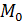с координатами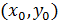

Уравнение касательной имеет вид

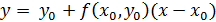
Двигаясь вдоль этой касательной, получим приближенное значение решения в точке :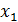

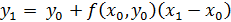
или

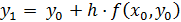(4)

Располагая приближенным решением в точке 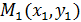можно повторить описанную ранее процедуру: построить прямую проходящую через эту точку с угловым коэффициентом 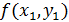, и по ней найти приближенное значение решения в точке .

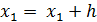Заметим, что эта прямая не является касательной к реальной интегральной кривой, поскольку точка 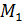нам не доступна, однако если 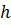достаточно мало то получаемые приближенные будут близки к точным значениям решения.

Продолжая эту идею, построим систему равно отстоящих точек

.

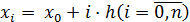Получение таблицы значений искомой функции 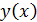по методу Эйлера заключается в циклическом применение формулы

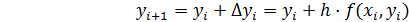(5)

Рисунок. 1. Геометрическая иллюстрация метода Эйлера

Решение ОДУ в некоторой точке x_i называется устойчивым, если найденное в этой точке значение функции y_i мало изменяется при уменьшении шага интегрирования. Для проверки устойчивости, таким образом, надо провести два расчета значения (y_i) – с шагом интегрирования 2h и при уменьшенной (например, двое) величине шага. В качестве критерия устойчивости можно использовать малость относительного изменения полученного решения при уменьшении шага интегрирования

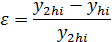
где 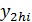- решение, рассчитанное с шагом 2h , 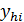– решение, рассчитанное с

шагом h .

Пример

В качестве примера проведем расчеты по формулам метода Эйлера с

шагом h=0,05 и h=0,1 для задачи Коши .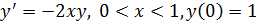

Формулы для расчета имеют вид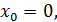

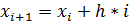
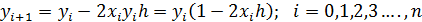
Рассчитываем с шагом h = 0.1

0.

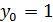
1.

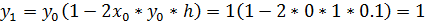
2.

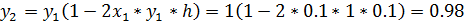
3.

***

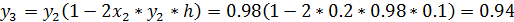
10.