Относительное позиционирование

Суть такого позиционирования заключается в определении координат пункта В (рис.2) относительно координат пункта А. Тогда можно записать, что:

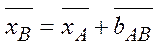(1.63)

где: 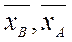соответственно векторы координат пунктов А и B, а вектор АB называют базелинией (baseline) 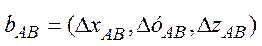определяется одновременными наблюдениями на пунктах A и B соответственно.

A Рис.1.23 B

Принимая одновременное наблюдение спутников j и k с пунктов A и B можно сформулировать следующие линейные фазовые разности

а) сингл – разности – разности первого порядка

б) дубль – разности – разности второго порядка

в) трипл – разности – разности третьего порядка

Разности фаз

А) сингл – разности (разности первого порядка)

Эти разности представляют интерес с теоретической точки зрения.

В соответствии с (1.61) можно записать

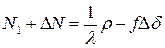(1.64)

Для наблюдений с одного спутника на точки А и В можно составить

следующую систему

(1.65)

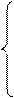
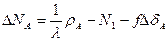
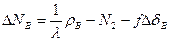
и найти разность 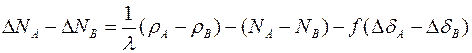(1.66)

Обозначая

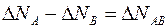(1.67)

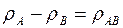(1.68)

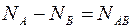(1.69)

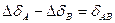, (1.70) уравнение (1.66) можно записать так

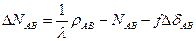
Это есть первая разность фаз – сингл-разность

Достоинством первой разности является то, что , что в ней отсутствует задержка часов спутников.

Такие разности можно записать для спутников j и k

(1.71)

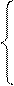
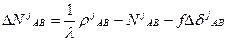
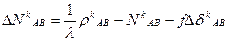
Б) дубль – разности (разности второго порядка)

Для того чтобы изъять временную задержку часов приемников составляют вторые разности.

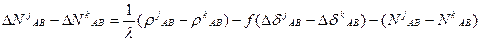
Здесь

,

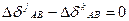т.к. будет ликвидирована задержка времени часов приемников

(1.73)

,

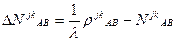где

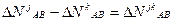(1.74)

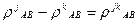
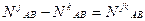
Пусть наблюдается 4 спутника. Для них можно составить 3 уравнения вида(1.73) с неизвестными: ∆x, ∆y, ∆z, 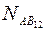, , 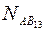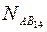. Поскольку число неизвестных больше числа уравнений, то их составляют для двух близких эпох, при которых числа неоднозначности остаются одними и теми же. Тогда число уравнений будет уже равным числу неизвестных. Если их составить больше , то решение можно выполнить по методу наименьших квадратов

В) трипл – разности (разности третьего порядка)

Если записать дубль – разность для эпох t_{1 и t2}

(1.75)

(1.76)

тогда триппл – разность будет иметь вид

(1.77)

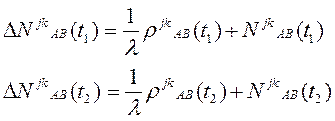
Статическое относительное позиционирование

В этом (статическом) позиционировании измерение вектора АВ выполняется установкой двух приемников на эти пункты в течение всего периода наблюдений. Заданием в данном случае является установление числа неизвестных и числа уравнений, затем всё сводится в сою очередь к установлению числа необходимых спутников и числа эпох. Рассмотрим это для каждой разности фаз отдельно.

Сингл – разности.

Исходным здесь является уравнение

(1.78)

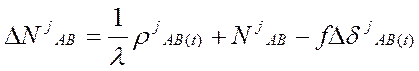
Обозначим число спутников n_j, число эпох n_t.

(1.79)

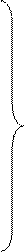
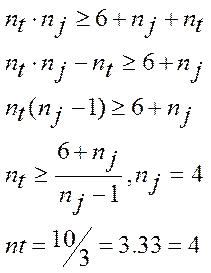
Дубль – разности.