Продольная деформация прямолинейного стержня
Рассмотрим задачу о растяжении-сжатии прямого стержня, произвольного поперечного сечения (в общем случае переменного по длине). Совместим ось  с осью симметрии стержня. Начало координат поместим в один из концов стержня, вся длина которого равна
с осью симметрии стержня. Начало координат поместим в один из концов стержня, вся длина которого равна  . Пусть
. Пусть 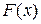 – функция, показывающая изменение площади поперечного сечения стержня,
– функция, показывающая изменение площади поперечного сечения стержня,  – модуль упругости материала, который предполагается однородным и изотропным. Пусть на стержень по всей длине в направлении
– модуль упругости материала, который предполагается однородным и изотропным. Пусть на стержень по всей длине в направлении  действует сплошная нагрузка, интенсивностью
действует сплошная нагрузка, интенсивностью  (одинаковая в каждой точке поперечного сечения).
(одинаковая в каждой точке поперечного сечения).
 |
Под действием этой нагрузки стержень растягивается или сжимается. Предположим, что все сечения, нормальные к оси стержня в его недеформированном состоянии, остаются плоскими (не искажаются) и сохраняют свою перпендикулярность к оси в процессе растяжения-сжатия (гипотеза плоских сечений).
В этом случае можно приближенно считать, что точки поперечного сечения, находящегося на расстоянии  от начала координат, получат одинаковое перемещение
от начала координат, получат одинаковое перемещение  . Сечение, находящееся на расстоянии
. Сечение, находящееся на расстоянии 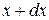 , получит перемещение
, получит перемещение 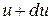 . Координата выбрана произвольно, так что имеем функцию продольных перемещений
. Координата выбрана произвольно, так что имеем функцию продольных перемещений  точек оси стержня. Тогда относительное удлинение элемента
точек оси стержня. Тогда относительное удлинение элемента 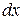 будет равно
будет равно

– геометрическое уравнение.
Также из гипотезы плоских сечений следует, что в поперечных сечениях действуют только нормальные напряжения  , одинаковые во всех точках сечения. Равнодействующая этих напряжений равна
, одинаковые во всех точках сечения. Равнодействующая этих напряжений равна
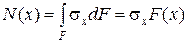 ,
,
где  – площадь поперечного сечения с координатой
– площадь поперечного сечения с координатой  .
.
Нормальные напряжения связаны с продольными деформациями физическим соотношением (закон Гука)

(или 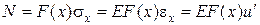 )
)
Уравнение равновесия можно составить, рассматривая элементарный отрезок стержня 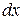 , находящийся под действием внешней нагрузки
, находящийся под действием внешней нагрузки  и внутренних усилий:
и внутренних усилий: 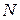 – слева и
– слева и  – справа.
– справа.
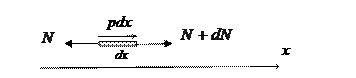 |
Проектируя эти силы на ось  , получим
, получим
 или
или  .
.
Будем считать, что продольные деформации стержня стеснены упругим основанием с коэффициентом  . (Это значит, что существует упругая среда, обладающая тем свойством, что возникающие с её стороны реакции пропорциональны перемещениям и равны
. (Это значит, что существует упругая среда, обладающая тем свойством, что возникающие с её стороны реакции пропорциональны перемещениям и равны 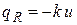 ).
).
Тогда, уравнение равновесия будет иметь вид
 (1)
(1)
– уравнение равновесия.
Для того чтобы задача была поставлена корректно, надо к данному уравнению добавить граничные условия.
В данной одномерной задаче область, занимаемая упругим телом – отрезок прямой  , а граница области состоит из двух точек
, а граница области состоит из двух точек 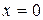 и
и 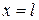 . Направляющие косинусы внешней нормали в этих точках равны
. Направляющие косинусы внешней нормали в этих точках равны 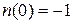 и
и  .
.
Можно рассматривать граничные условия двух видов. Если на соответствующих концах стержня заданы сосредоточенные силовые воздействия  и
и 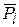 , то имеем статические краевые условия. Если в точках
, то имеем статические краевые условия. Если в точках 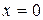 и
и 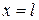 заданы перемещения
заданы перемещения 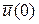 и
и 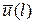 , то имеем кинематические граничные условия.
, то имеем кинематические граничные условия.
| Статические краевые условия | Кинематические краевые условия |
 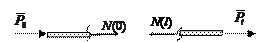 |  (2) (2) |
Параметры 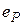 и
и  задаются на каждом конце стержня и принимают значения 0 или 1, в зависимости от решаемой задачи, причем
задаются на каждом конце стержня и принимают значения 0 или 1, в зависимости от решаемой задачи, причем  . Смысл этих параметров определяется индексом, так, например,
. Смысл этих параметров определяется индексом, так, например,  , если на соответствующем конце задана внешняя сосредоточенная сила
, если на соответствующем конце задана внешняя сосредоточенная сила  , тогда как, перемещение
, тогда как, перемещение  там не фиксируется.
там не фиксируется.
Например, для стержня, у которого один конец закреплен, другой свободен, будем иметь
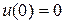 ,
,  .
.
Математическая модель (1), (2) называется краевой задачей для перемещений.
Существует и другая математическая модель описывающая ту же задачу.
Найдем полную потенциальную энергию данной механической системы
 ,
,
где 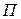 – потенциальна энергия деформации при растяжении-сжатии,
– потенциальна энергия деформации при растяжении-сжатии,  – работа внешних сил.
– работа внешних сил.
В данном случае
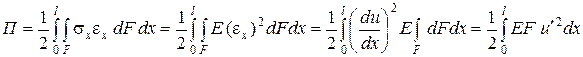 ,
,
Работа сил упругого основания равна
 .
.
Работа, которую производит заданная распределенная нагрузка и заданные сосредоточенные на концах силы равна
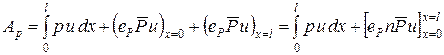 .
.
Таким образом, функционал полной потенциальной энергии (функционал Лагранжа) для данной задачи принимает вид
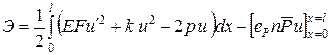 . (3)
. (3)
Таким образом, математическая модель для решения той же задачи определения смещений в стержне, находящемся под действием продольно распределенных сил, может быть сведена к нахождению минимума функционала полной потенциальной энергии (3), с учетом краевых условий (2). Такая задача называется вариационной.
Найдем связь между вариационной и краевой задачами. Вычислим первую вариацию функционала, и приравняет её к нулю.
 .
.
Применим к первому интегралу формулу интегрирования по частям:
 .
.
Таким образом, получаем
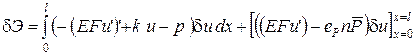 .
.
Функционал Лагранжа определен на кинематически допустимых перемещениях, следовательно, допустимая к рассмотрению вариация  отлична от нуля на конце стержня, если на этом конце
отлична от нуля на конце стержня, если на этом конце  и
и  , тогда
, тогда
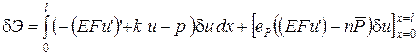 .
.
Используя основную лемму вариационного исчисления, из условия  получаем уравнение Эйлера для этого функционала
получаем уравнение Эйлера для этого функционала

(уравнение равновесия)
и естественные краевые условия:
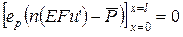 , т.к.
, т.к. 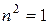 .
.
(статические краевые условия).
Рассмотрим частный случай внешней нагрузки и однородных граничных условий. Пусть  – вес тела, а коэффициент упругого основания не зависит от x, т.е.
– вес тела, а коэффициент упругого основания не зависит от x, т.е. 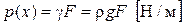 (
( 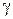
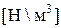 – удельный вес материала
– удельный вес материала 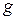
 – ускорение свободного падения),
– ускорение свободного падения), 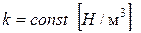 .
.
Пример 1.
Бетонный стержень конической формы заделан нижним концом и испытывает воздействие собственного веса. Высота стержня равна 3 м, радиус нижнего основания 0,5 м, верхнего основания 0,25 м. 
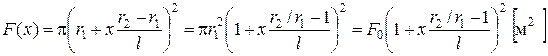 .
.
Данные: 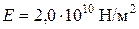 ,
, 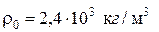 ,
,  ,
,
 (плотный грунт),
(плотный грунт), 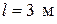 ,
,  ,
, 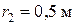 .
.
Определить перемещения и внутренние усилия. Рассмотреть два метода: 1) метод Ритца; 2) метод конечных элементов.
Математическая модель задачи имеет вид
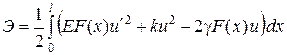 ,
,
 ,
, 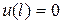 .
.
1) Метод Ритца
Перейдем в функционале полной потенциальной энергии и граничных условиях к безразмерным величинам по формулам
 .
.
Тогда,
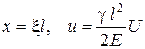 ,
,
 ,
, 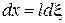 ,
,  ,
,  .
.
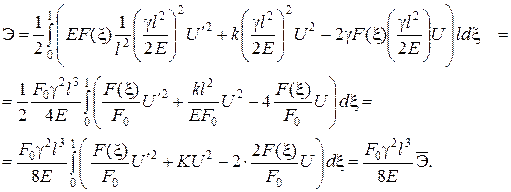
Здесь 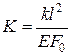 ,
,  – площадь поперечного сечения при
– площадь поперечного сечения при  .
.
Таким образом, получаем задачу о минимуме функционала
 ,
,
с граничными условиями
 ,
,  .
.
Решение ищем в виде,
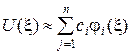
где в качестве базисных функций выбираем систему функций
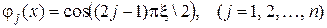 .
.
Решение задачи (без учета упругого основания)

2) Метод конечных элементов.
Математическая модель задачи:
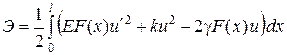 ,
,
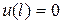 .
.
Система метода конечных элементов будет иметь вид:
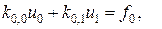
 ,
,
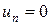
где
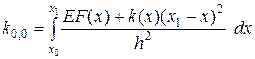 ,
,
 ,
,
 ,
,
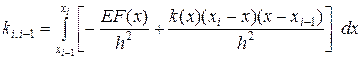 ,
,
 ,
,
 ,
,
 ,
, 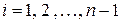 .
.
Пример 2.
Рассчитать ступенчатый брус с исходными данными, приведенными на рисунке.
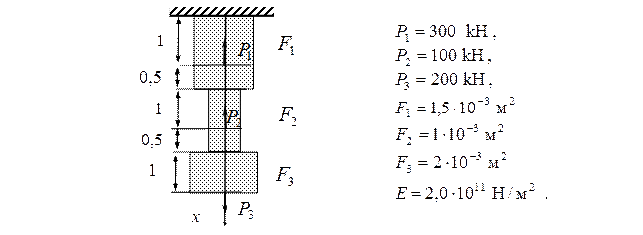
Математическая модель задачи:
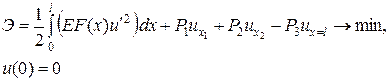 ,
,
Система метода конечных элементов для пяти элементов будет иметь вид:

где
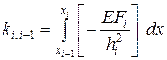 ,
,
 ,
,
 ,
, 
, 
