Исследование напряженного состояния при известных главных напряжениях

В предыдущем параграфе было указано, что для исследова­ния напряженного состояния должны быть известны напряже­ния на любых трех взаимно перпендикулярных площадках, проходящих через данную точку. Математическая сторона та­кого исследования наиболее проста, когда исходные напряже­ния, т. е. напряжения, известные в начале исследования,— главные.

Наибольшее касательное напряжение:

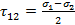(для площадок параллельных σ₃)

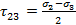(для площадок параллельных σ₃)

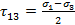(для площадок параллельных σ₃)

Вспоминая правило индексов, согласно которому σ₁≥ σ₂≥ σ₃, заключаем, что из трех, так сказать, частных максиму­мов τ наибольшим, т. е. действительно максимальным для данной точки тела, оказывается τ₁₃.

Сделаем еще один вывод : в частном слу­чае при σ₂= σ₃=0 ни на одной площадке исследуемой серии не возникает касательных напряжений, т. е. все площадки этой се­рии главные.

Если все три главных напряжения равны между собой: σ₁= σ₂= σ₃, то для данной точки тела любая проходя­щая через нее площадка главная.

Рассмотрим частный случай плоского напряженного со­стояния, для которого отличные от нуля главные напряжения равны по модулю и противоположны по знаку

Такое напряженное состояние носит название чистого сдвига (происхождение этого названия разъяснено несколько ниже).

Чистый сдвиг — единственный случай плоского напряженно­го состояния, когда через точку можно провести две взаимно перпендикулярные площадки, на которых касательные напря­жения максимальны, а нормальные напряжения отсутствуют.

Итак, наряду с определением:

чистый сдвиг — это частный случай плоского напряженного состояния, при котором не равные нулю главные напряжения равны по значению и противоположны по знаку,

— возможно и другое определение, вытекающее из проведен­ного исследования: чистым сдвигом называют такое плоское напряженное состояние, при котором в окрест­ности данной точки можно выделить элемент таким образом, чтобы на четы­рех его гранях были толь­ко равные между собой касательные напряжения.

Это последнее опре­деление можно рассмат­ривать как объяснение названия, принятого для данного напряженного со­стояния.

Часто встречается такое напряженное состояние, при котором одна пара взаимно перпендикулярных граней единичного кубика свободна от напряжений, как это показано на рис. 2.3.2, а.. .в.

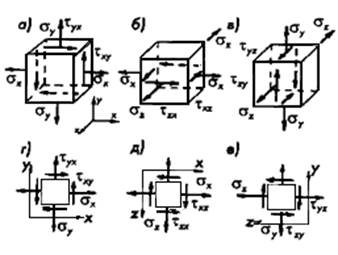
Рисунок 2.3.2

Такое напряженное состояние оказывается плоским. Матрицы тензоров напряжений в таких случаях представляются следующим образом:

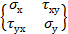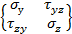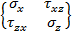; ; (2.3.3)

Заметим, что площадка, на которой нет никаких напряжений, должна рассматриваться как главная, так как при нулевом значении Нормального напряжения на ней нет и касательных напряжений.

На рис. 2.3.2, г...е даны принятые в современной литературе схематические изображения нескольких видов плоского напряженного состояния, которые соответствуют схемам на рис. 2.3.2, а...в.

В сопротивлении материалов используется также понятие линейного напряженного состояния, когда два из трех главных напряжений равны нулю. Нетрудно видеть, что под эту классификацию подходят только простое растяжение и простое сжатие.

Деформация стержня

Под действием внешних сил прямолинейный стержень может несколько увеличить свою первоначальную длину‚ оставаясь прямым. Разность между текущей l и начальной длиной l₀ ‚ обозначим через ∆ l и назовем деформацией удлинения или абсолютной деформацией растяжения стержня, рис. 2.3.3, а. По аналогии вводится понятие деформации укорочения или деформации сжатия стержня, рис. 2.3.3, б. Отношение абсолютной линейной деформации стержня (элемента) к его первоначальной длине называется линейной деформацией:

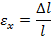
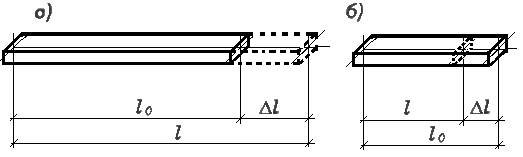
Рисунок 2.3.3

В некоторых случаях стержни деформируются так, что поперечные сечения, оставаясь параллельными, поворачиваются на некоторый угол относительно друг друга вокруг продольной оси. Например в соответствии со схемами на рис 2.3.4.а, 2.3.4, б сечение В стержня АВ поворачивается относительно сечения А на угол φ. В этом случае говорят о деформации кручения стержня, а угол называется углом закручивания.

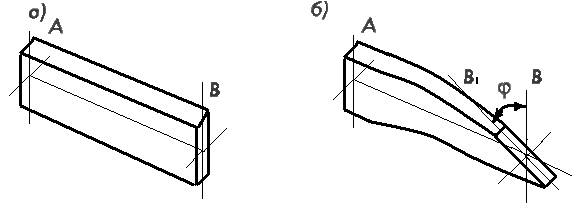
Рисунок 2.3.4

При деформации изгиба первоначально прямой стержень искривляется, а поперечные сечения поворачиваются вокруг осей, перпендикулярных продольной оси стержня. рис. 2.3.5, а и 2.3.5. б. На последнем через Ɵ обозначен угол поворота одного концевого сечения относительно другого вокруг поперечной оси z.

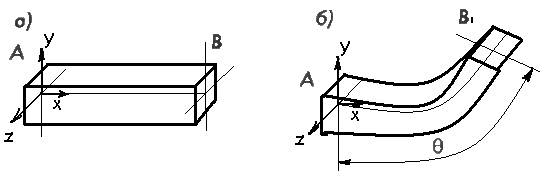
Рисунок 2.3.5

Нередко бывают комбинации изгиба с кручением, а также с растяжением или с сжатием.

Деформируемое твердое тело можно представить себе разбитым на множество плотно прилегающих друг к другу малых параллелепипедов. Деформацию каждого такого элемента обычно описывают тремя компонентами линейных деформаций ε_x, ε_y, ε_z и шестью компонентами сдвигов (угловых деформаций) γ_xy, γ_yx, γ_yz, γ_zy, γ_zx, γ_xz.

Можно показать, что γ_xy= γ_yx, γ_yz= γ_zy, γ_zx= γ_xz

Таким образом, имеем по существу всего шесть компонентов деформированного состояния.

Продолжая аналогию между теорией напряжений и теорией деформаций, можно утверждать, что в каждой точке тела существует три взаимно перпендикулярные направления главных деформаций. В главных осях деформации сдвиги равны нулю, и элементарный параллелепипед, выделенный плоскостями, перпендикулярными этим осям, переходит в другой прямоугольный параллелепипед без искажения углов между взаимно перпендикулярными ребрами.

В изотропном теле направления главных напряжений и главных деформаций совпадают.

Деформации безразмерные и для реальных строительных материалов достаточно малы и имеют порядок ε≈10^-3 , γ≈10^-4…10^-3