Касательные напряжения при изгибе
Плоский изгиб.
Пусть во всех поперечных сечениях стержня N= 0; Мy=0; Mx≠0 и стержень изгибается в главной плоскости уz. Изгиб стержня в одной из главных плоскостей называют главным плоским изгибом или просто плоским изгибом.
Рассмотрим более детально плоский изгиб участка стержня моментом М=const (рис. 2.7.1). Такой случай нагружения называется чистым изгибом.
Нормальные напряжения в точках сечения определяются по формуле:
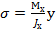 (2.7.1)
(2.7.1)
где σ – нормальные напряжения в точке;
Мх – момент относительно оси х;
Jx – момент инерции относительно оси х;
у – расстояние от оси х до точки.
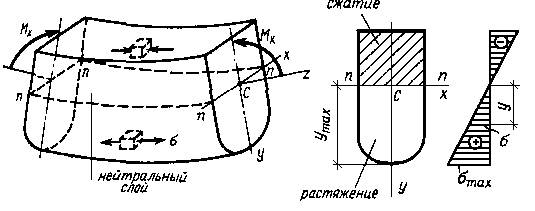
Рисунок 2.7.1
По высоте сечения имеем две зоны — растяжения и сжатия, их разделяет нейтральный слой, продольные волокна которого искривляются, но не меняют свое длины (σ = 0). Линия пересечения нейтрального слоя с плоскостью поперечного сечения п—п называется нейтральной или нулевой линией. В данном случае она совпадает с осью х и проходит через центр тяжести сечения С.
Остановимся кратко на условиях применения формулы 2.7.1. Если на поверхности балки (или ее модели) перед изгибом нанести ортогональную сетку продольных и поперечных линий, то можно увидеть, что в среднем участке, где балка испытывает чистый изгиб ( Mx=const и Qx=0), поперечные линии остаются прямыми ортогональными к продольным линиям сетки (рисунок 2.7.2)
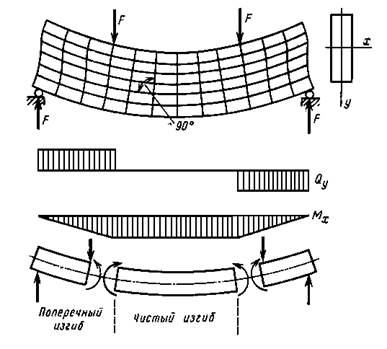
Рисунок 2.7.2
На участке поперечного изгиба из-за влияния поперечных сил сечения балки слегка искривляются (на рисунке это искривление слегка преувеличено). Поэтому применение гипотезы плоских сечений слегка преувеличено.
Более точный анализ показывает, что отклонение фактической эпюры от линейной эпюры σ, определяемой формулой (2.7.1), зависит от отношения длины и высоты балки l/h. На рисунке 2.7.3, а, б дано сравнение эпюр σ для двух балок, имеющих разное значение l/h.
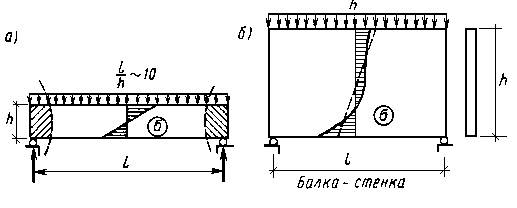
Рисунок 2.7.3
При малом отношении l/h формула (2.7.1) неприменима. На рис. 2.7.3,б фактическая эпюра σ показана сплошной линией, а по формуле (2.7.1) пунктирной линией. Обычно считается, что ею можно пользоваться с достаточной точностью при l/h ≈8…10 (рис. 2.7.3,а). Но даже в балке с большим l/h она может давать заметную погрешность в областях приложения сосредоточенных сил типа опорных реакций (на рис. 2.7.3,а эти области отмечены штриховкой). Здесь заметное влияние оказывает нарушение и гипотезы плоских сечений, и гипотезы о не надавливания продольных волокон.
Расчеты на прочность по нормальным напряжениям.
Наибольшее нормальное напряжение при плоском изгибе возникает в точке, наиболее удаленной от нулевой линии (у=уmax) Условие прочности по нормальным напряжениям записывается в следующем виде:
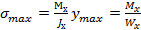 (2.7.2)
(2.7.2)
Касательные напряжения при изгибе.
В общем случае в поперечных сечениях балки при плоском поперечном изгибе возникают два силовых фактора: изгибающий момент Мx и поперечная сила Qy (риc. 2.7.4)
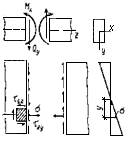
Рисунок 2.7.4
Первый реализуется в поперечном сечении системой нормальных напряжений 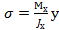
Поперечная сила Qy вектор которой лежит в плоскости поперечного сечения, вызывает в точках сечения касательные напряжения τху. По закону о парности касательных напряжений на продольных площадках возникают равные им напряжения τху= τуz= τ.
Напряжения τху возникают вследствие деформации среза продольных волокон балки, в то время как напряжения τуz,. порождены деформацией сдвига продольных волокон вдоль балки. Благодаря напряжениям τ, возникающим на продольных и поперечным площадкам, балка работает на изгиб не как отдельные продольные волокна, а как сплошное монолитное тело.
Действительно, сопоставим работу сплошной балки (рис.2.7.5,а) и балки, разрезанной рядом горизонтальных сечений на отдельные слои (рис. 2.7.5, г).
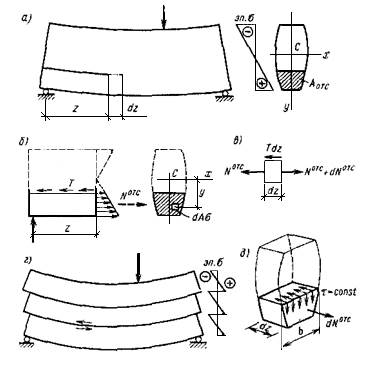
Рисунок 2.7.5
В последней наблюдаются проскальзывания по плоскостям разрезов, и если пренебречь силами трения, то каждый слой будет изгибаться как самостоятельная балка, а эпюра напряжений σ по высоте сечения будет иметь разрывы. В сплошной балке (рис. 2.7.5, а, б) по продольному сечению возникают усилия сдвига, интенсивность которых обозначим Т (усилие, приходящееся на единицу длины, Н/м). Благодаря взаимодействию с усилиями Т устраняются относительные проскальзывания частей балки, соприкасающихся по продольному сечению, и балка работает на изгиб как сплошное монолитное тело, а эпюра σ изменяется по высоте сечения без скачков в соответствии с формулой 2.7.1.
Усилия сдвига Т и соответствующие им напряжения τ найдем из условия равновесия отсеченной части балки показанной на рис. 2.7.5,б, сделав допущение о том, что касательные напряжения τ по ширине сечения b распределены равномерно (рис.2.7.5, д), после чего найдем:
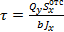 (2.7.3)
(2.7.3)
Во многих случаях максимальные касательные напряжения в поперечном сечении возникают на уровне нейтрального слоя балки, т.е. в точках, где нормальные напряжения от изгибающего момента равны нулю (см.рисунки 2.7.6,б и 2.7.7,в)
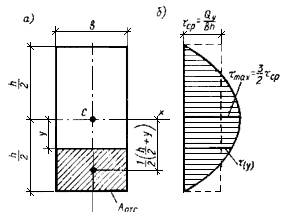
Рисунок 2.7.6
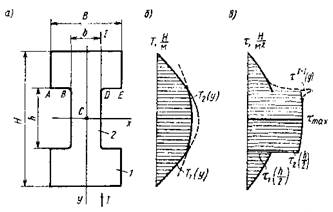
Рисунок 2.7.7
Необходимо заметить, что в некоторых случаях могут оказаться опасными такие точки сечения, в которых возникают нормальные и касательные напряжения, каждое из которых не является наибольшим в сечении. Проверка прочности в таких случаях проводится с использованием соответствующей теории прочности.
