Новое определение вектора
Пусть имеется вектор 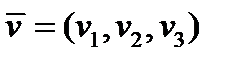 . Подобно тому, как точку с координатами
. Подобно тому, как точку с координатами  для краткости обозначают через
для краткости обозначают через 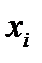 , вектор с компонентами
, вектор с компонентами  обозначим через
обозначим через 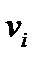 . При переходе к новой системе координат компоненты вектора преобразуются по формуле:
. При переходе к новой системе координат компоненты вектора преобразуются по формуле:
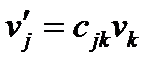 (40)
(40)
Проиллюстрируем применение символа Кронекера для обращения формулы (40). Умножим обе части (40) на  :
:
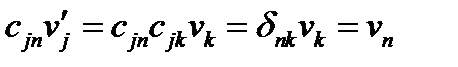 , т.е.
, т.е.
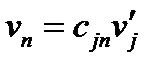 (41)
(41)
При выводе (41) мы использовали формулы (36) и (39). Формулы (40) и (41) положены в основу нового определения вектора.
Определение. Вектор – это геометрический объект, который в любой прямоугольной системе координат определяется тремя числами – его компонентами, которые при преобразовании системы координат преобразуются по формулам (40) и (41).
Вектор существует независимо от системы координат, он инвариантен, а вот его координаты меняются при преобразованиях системы координат. Новое определение вектора сохраняет все известные из курса линейной алгебры операции с векторами:
1) Сложение векторов:
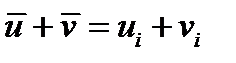 (42)
(42)
2) Сложение ассоциативно, т.е.
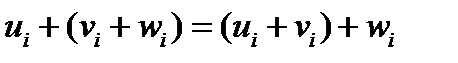 (43)
(43)
3) Умножение вектора на скаляр:
 (44)
(44)
4) Дистрибутивность умножения:
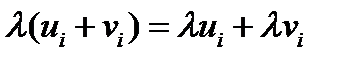 (45)
(45)
Если компоненты вектора 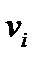 зависят от некоторого параметра
зависят от некоторого параметра 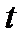 , то производные
, то производные  тоже образуют вектор
тоже образуют вектор 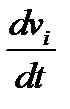 , который называется производной исходного вектора
, который называется производной исходного вектора 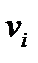 по
по 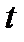 . Аналогично определяется и производная более высокого порядка вектора по скалярному параметру.
. Аналогично определяется и производная более высокого порядка вектора по скалярному параметру.
Рассмотрим скалярное произведение двух векторов 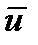 и
и 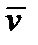 :
:
 (46)
(46)
Докажем, что скалярное произведение – скаляр и инвариантно относительно преобразования системы координат. В новой системе координат компоненты векторов обозначим  и
и 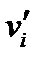 . Тогда скалярное произведение будет равно:
. Тогда скалярное произведение будет равно:
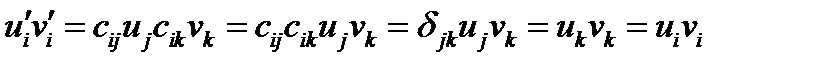 (47)
(47)
Модуль вектора, определяемый скалярным произведением вектора самого на себя, запишется так:
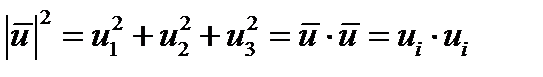 (48)
(48)
Записывать квадрат модуля в виде 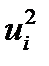 нецелесообразно, т.к. при такой записи не ясно, что
нецелесообразно, т.к. при такой записи не ясно, что  представляет собой немой индекс. Вектор, модуль которого равен единице, называется, как известно, единичным вектором или ортом. Направление в пространстве обычно задается единичным вектором. Рассмотрим единичный вектор
представляет собой немой индекс. Вектор, модуль которого равен единице, называется, как известно, единичным вектором или ортом. Направление в пространстве обычно задается единичным вектором. Рассмотрим единичный вектор  . Скалярное произведение
. Скалярное произведение 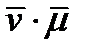 определяет проекцию
определяет проекцию 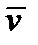 на направление
на направление  :
:
 (49)
(49)
Поскольку компонентами единичного вектора являются направляющие косинусы  ,
,
или короче 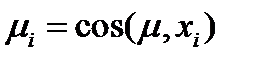 , (50)
, (50)
то 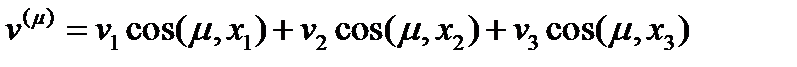 (51)
(51)
Формула (51) линейна и однородна относительно направляющих косинусов. Она означает, что для любого направления в пространстве  каждому вектору можно поставить в соответствие скаляр – проекцию вектора на это направление, посредством линейного и однородного относительно направляющих косинусов соотношения. Выясним, какой смысл имеют числа
каждому вектору можно поставить в соответствие скаляр – проекцию вектора на это направление, посредством линейного и однородного относительно направляющих косинусов соотношения. Выясним, какой смысл имеют числа  в (51). Совместим направление
в (51). Совместим направление  с положительным направлением оси
с положительным направлением оси  . Тогда
. Тогда 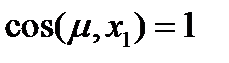 , а
, а 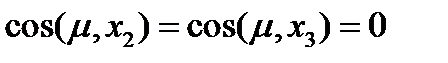 и
и  , т.е.
, т.е.  – это проекция вектора
– это проекция вектора  на направление оси
на направление оси  . Аналогично доказывается, что
. Аналогично доказывается, что 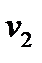 и
и  – это проекции вектора на две другие оси. Следовательно, проекция вектора на произвольное направление определяется его проекциями на три фиксированных направления координатных осей.
– это проекции вектора на две другие оси. Следовательно, проекция вектора на произвольное направление определяется его проекциями на три фиксированных направления координатных осей.
Формула (51) будет играть в дальнейшем определяющую роль, поскольку она допускает далеко идущие обобщения.
§8. Задачи.
Задача 1. Старая система координат 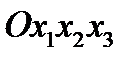 преобразуется к новой системе
преобразуется к новой системе  , заданной следующими углами:
, заданной следующими углами: 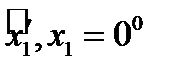 ,
,  ,
, 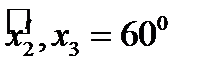 ,
, 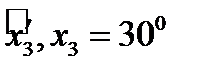 . Написать матрицу преобразования и проверить ее ортогональные свойства.
. Написать матрицу преобразования и проверить ее ортогональные свойства.
Решение. Имеем:
 ,
, 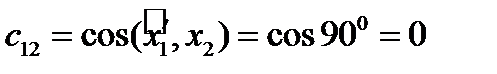 ,
,
 ,
,  ,
,
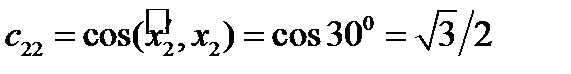 ,
, 
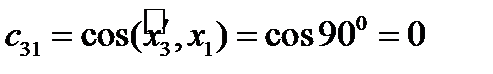 ,
, 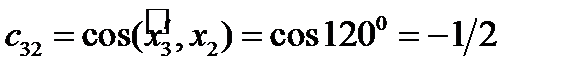 ,
,
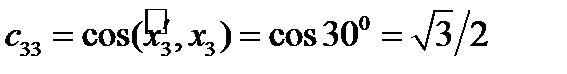 .
.
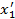 |
 |
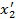 |
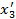 |
 |
| Рис.5 |
 |
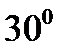 |
 (52)
(52)
 |
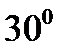 |
Задача 2. Пусть новая система координат получена из старой в результате вращения вокруг оси 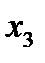
 на угол
на угол 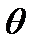 против часовой стрелки. Написать матрицу преобразования.
против часовой стрелки. Написать матрицу преобразования.
Решение.
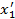 |
 |
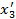 |
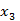 |
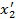 |
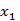 |
| Рис.6 |
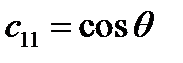 ,
,  ,
,
 |
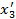 |
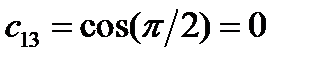 ,
,
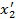 |
 ,
, 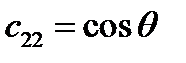 ,
, 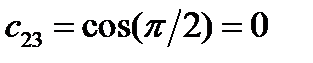 ,
,
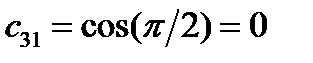 ,
,  ,
,
 |
 |
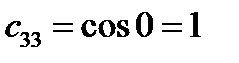
Тогда матрица преобразования имеет
 |
 |
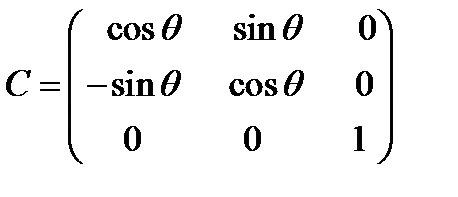 (53)
(53) Задача 3. Исследовать влияние преобразования координат
 |
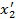 |
 |
| Рис.7 |
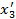 |
 |
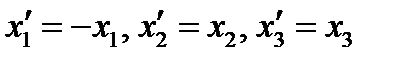 на компоненты вектора.
на компоненты вектора.
 |
 |
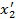 |
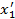 |
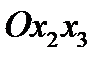 . Первоначальная правая система координат
. Первоначальная правая система координат 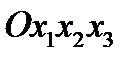 преобразуется в левую
преобразуется в левую 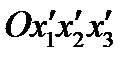 . Матрица преобразования имеет вид:
. Матрица преобразования имеет вид: 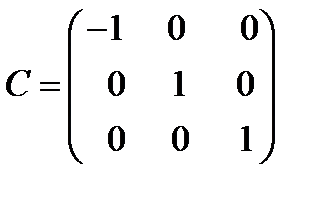 (54)
(54) Вектор преобразуется по формуле (40):
 (55)
(55)
или 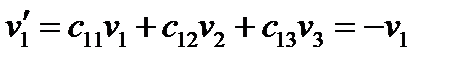

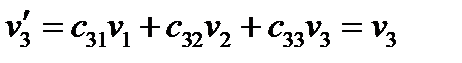
Таким образом, указанная инверсия изменяет только компоненту 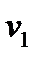 , две другие компоненты при этом не меняются.
, две другие компоненты при этом не меняются.
Задача 4. Найти преобразование компонент вектора при вращении, описанном в задаче 2.
Решение. Используя матрицу преобразования (53) и формулу (55), получим:
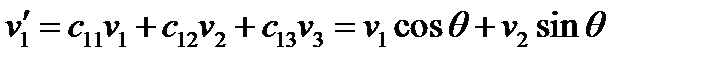
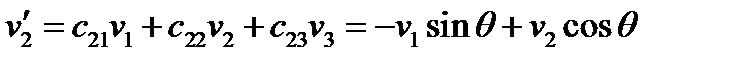 (56)
(56)

Задача 5.. Доказать равенство 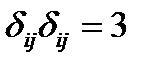 (57)
(57)
Решение. Имеем:
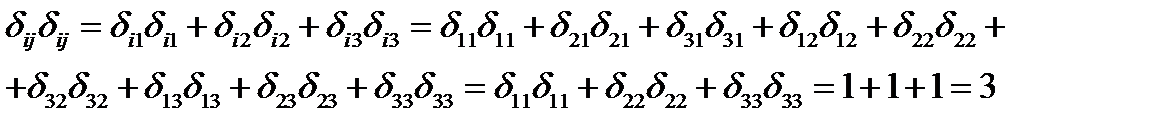
Задача 6. Компоненты единичного вектора  являются непрерывно дифференцируемыми функциями параметра
являются непрерывно дифференцируемыми функциями параметра 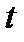 . Показать, что вектор
. Показать, что вектор  перпендикулярен вектору
перпендикулярен вектору  .
.
Решение. Необходимо доказать, что скалярное произведение  . Имеем:
. Имеем:
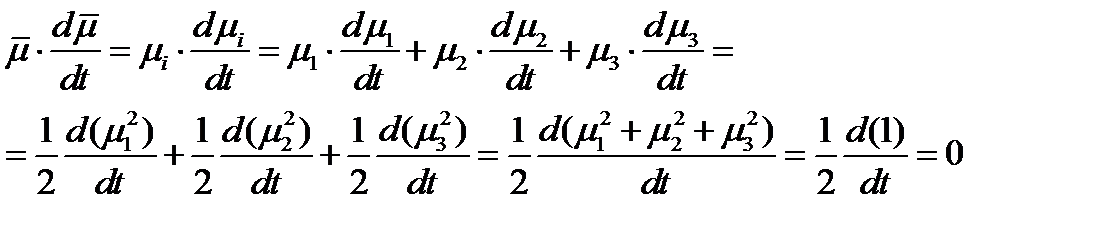
Задача 7. Доказать, что каждый элемент ортогональной матрицы преобразования  равен своему алгебраическому дополнению, взятому со знаком плюс или минус.
равен своему алгебраическому дополнению, взятому со знаком плюс или минус.
Решение. Матрица перехода от старой системы координат к новой имеет вид (15). Ее определитель, как было показано в параграфе 3, равен  , где знак плюс берется в том случае, если старая и новая системы координат имеют одинаковую ориентацию (например, обе правые) и знак минус – в противном случае. По определению обратной матрицы имеем:
, где знак плюс берется в том случае, если старая и новая системы координат имеют одинаковую ориентацию (например, обе правые) и знак минус – в противном случае. По определению обратной матрицы имеем:
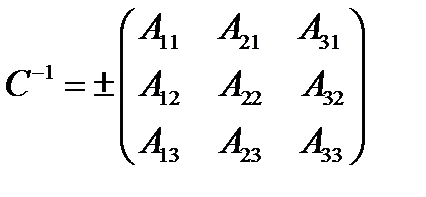
где  – алгебраическое дополнение элементов матрицы
– алгебраическое дополнение элементов матрицы 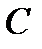 . С другой стороны, как было показано в параграфе 3, обратная матрица получается транспонированием прямой матрицы, т.е.
. С другой стороны, как было показано в параграфе 3, обратная матрица получается транспонированием прямой матрицы, т.е. 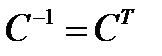 и имеет вид (17). Отсюда и получаем, что
и имеет вид (17). Отсюда и получаем, что 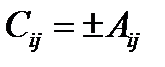 .
.
Подчеркнем еще раз, что знак плюс берется тогда, когда обе системы координат, старая и новая, имеют одинаковую ориентацию и знак минус – в противном случае.
Тензор второго ранга.
Вспомним задачу, приведшую нас в параграфе 1 к понятию тензора напряжений, и формулу (12). Сравним ее с формулой (51). Формула (51) любому направлению в пространстве 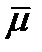 сопоставляет скаляр
сопоставляет скаляр 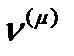 , который мы назвали проекцией вектора на направление
, который мы назвали проекцией вектора на направление  . Формула (12) идентична по структуре формуле (51), но с ее помощью любому направлению в пространстве
. Формула (12) идентична по структуре формуле (51), но с ее помощью любому направлению в пространстве 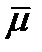 сопоставляется не скаляр, а вектор тоже посредством линейного и однородного относительно направляющих косинусов соотношения. Из этого и будем исходить. Итак, пусть любому направлению в пространстве
сопоставляется не скаляр, а вектор тоже посредством линейного и однородного относительно направляющих косинусов соотношения. Из этого и будем исходить. Итак, пусть любому направлению в пространстве 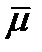 сопоставляется вектор
сопоставляется вектор 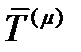 с помощью линейного и однородного относительно направляющих косинусов соотношения:
с помощью линейного и однородного относительно направляющих косинусов соотношения:
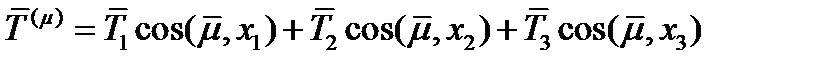 (58)
(58)
Геометрический объект с таким свойством называется тензором второго ранга и обозначается  . Вектор
. Вектор 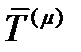 называется проекцией тензора на направление
называется проекцией тензора на направление 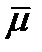 или значением тензора в этом направлении. Выясним, какой смысл имеют векторы
или значением тензора в этом направлении. Выясним, какой смысл имеют векторы  ,
, 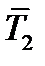 ,
, 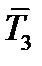 в формуле (58). Для этого совместим направление
в формуле (58). Для этого совместим направление 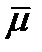 с направлением оси
с направлением оси  . Тогда
. Тогда  ,
,  ,
,  . Получаем, что проекция тензора
. Получаем, что проекция тензора  на ось
на ось  равна вектору
равна вектору  . Аналогично, совмещая направление
. Аналогично, совмещая направление 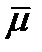 с направлением осей
с направлением осей  и
и 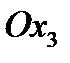 , получим, что векторы
, получим, что векторы 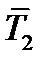 и
и 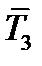 суть проекции тензора
суть проекции тензора  на оси
на оси  и
и 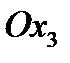 . Таким образом, в любой прямоугольной системе координат тензор
. Таким образом, в любой прямоугольной системе координат тензор  задается тремя векторами
задается тремя векторами  ,
, 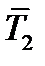 ,
, 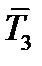 – своими проекциями на базисные направления. Компоненты векторов
– своими проекциями на базисные направления. Компоненты векторов  ,
, 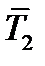 ,
, 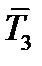 в системе координат
в системе координат 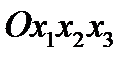 обозначим
обозначим  ,
, 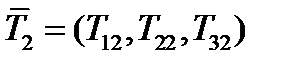 ,
,  .
.
Девять величин  называются компонентами тензора
называются компонентами тензора  в системе координат
в системе координат 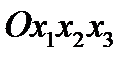 . Расположим их в виде матрицы:
. Расположим их в виде матрицы:
 , (59)
, (59)
которая называется матрицей тензора. Столбцы матрицы определяют три проекции тензора на координатные оси.
В другой системе координат 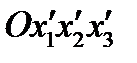 тензор
тензор  также определяется тремя проекциями
также определяется тремя проекциями 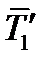 ,
,  ,
, 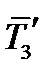 на новые координатные оси. Проекции тензора в новой и старой системах координат связаны друг с другом. Установим эту связь. Совместим в (58) направление
на новые координатные оси. Проекции тензора в новой и старой системах координат связаны друг с другом. Установим эту связь. Совместим в (58) направление 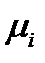 с направлением оси
с направлением оси  . Получим проекцию тензора на ось
. Получим проекцию тензора на ось 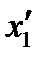 :
:
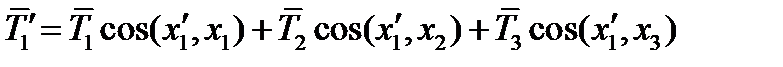 (60)
(60)
Совместив 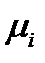 с направлением оси
с направлением оси 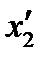 , получим
, получим
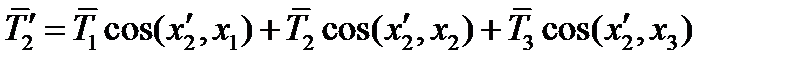 , (61)
, (61)
и наконец:
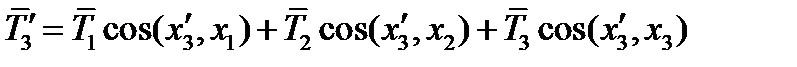 (62)
(62)
Стоящие в этих формулах косинусы – это элементы матрицы преобразования 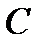 . Поэтому можно переписать:
. Поэтому можно переписать:

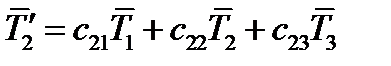 (63)
(63)
 .
.
Сокращенно это записывается так:
 ,
, 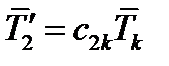 ,
, 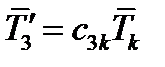 (64)
(64)
или еще короче: 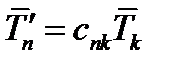 (65)
(65)
Видим, что закон преобразования проекций тензора такой же, как закон преобразования проекций вектора. Матрица тензора в новой системе координат состоит из компонент проекций тензора на эти новые оси. Первая проекция – вектор 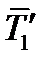 в новой системе имеет компоненты:
в новой системе имеет компоненты:  . Аналогично
. Аналогично 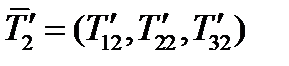 и
и  . Составленная из них матрица:
. Составленная из них матрица:
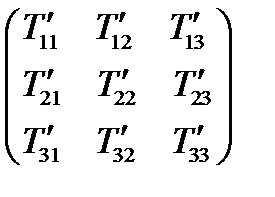 (66)
(66)
называется матрицей тензора в новой системе координат. Таким образом, матрица тензора  в старой системе состоит из компонент проекций тензора на старые оси, а в новой системе – из компонент проекций тензора на новые оси.
в старой системе состоит из компонент проекций тензора на старые оси, а в новой системе – из компонент проекций тензора на новые оси.
Установим связь между компонентами тензора в старой и новой системах координат. Обозначим компоненты векторов  в новом базисе через
в новом базисе через  , т.е.
, т.е.  . Компоненты векторов
. Компоненты векторов  в новом базисе выразим через старые по формулам преобразования вектора:
в новом базисе выразим через старые по формулам преобразования вектора:
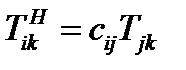 (67)
(67)
Тогда первое равенство (64) в новых координатах запишется так:
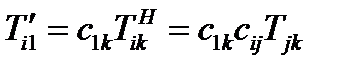 (68)
(68)
Аналогично, две другие формулы (64) в новых координатах будут выглядеть так:

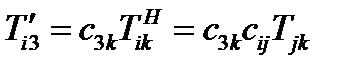 (69)
(69)
Или объединяя все три формулы:
 (70)
(70)
По формуле (70) преобразуются компоненты тензора при переходе от старой системы координат к новой. Выведем обратную формулу. Умножим обе части (70) на  , воспользуемся ортогональностью матрицы перехода и свойством символа Кронекера:
, воспользуемся ортогональностью матрицы перехода и свойством символа Кронекера:
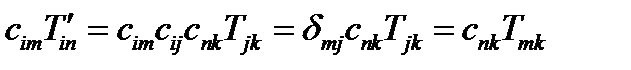 (71)
(71)
Умножим теперь обе части на 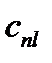 :
: 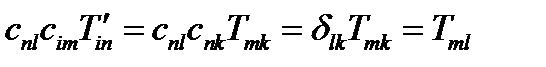
или  (72)
(72)
Формулы (70) и (72) определяют закон преобразования тензора второго ранга. Они положены в основу второго определения тензора. В любой прямоугольной системе координат тензор 2-го ранга определяется девятью компонентами, которые при преобразовании системы координат преобразуются по формулам (70) и (72).
