И интегрирование тензоров
В разделе математического анализа «Теория поля» изучались два простейших вида полей: скалярное и векторное. Теперь познакомимся с полем более сложной природы – тензорным полем. Тензорное поле ставит в соответствие каждой точке пространства 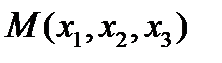 тензор
тензор 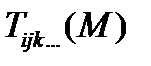 некоторого ранга. Компоненты тензора являются, как правило, непрерывными и дифференцируемыми функциями точки.
некоторого ранга. Компоненты тензора являются, как правило, непрерывными и дифференцируемыми функциями точки.
В прямоугольной декартовой системе координат 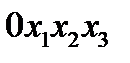 тензорное поле, например, 2-ого ранга задается девятью функциями координат. В дальнейшем для обозначения координат
тензорное поле, например, 2-ого ранга задается девятью функциями координат. В дальнейшем для обозначения координат 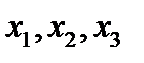 будем использовать одну букву
будем использовать одну букву 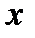 и компоненты тензорного поля
и компоненты тензорного поля 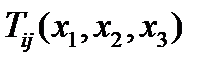 записывать в виде
записывать в виде 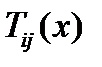 . Скалярные и векторные поля являются, соответственно, тензорными полями нулевого и первого рангов.
. Скалярные и векторные поля являются, соответственно, тензорными полями нулевого и первого рангов.
Дифференцирование компонент тензора по координате 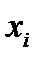 обозначается дифференциальным оператором
обозначается дифференциальным оператором 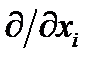 , или сокращенно
, или сокращенно 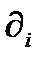 . Для производных второго порядка используется оператор
. Для производных второго порядка используется оператор 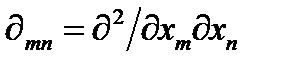 . Иногда частное дифференцирование по координате
. Иногда частное дифференцирование по координате 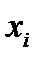 изображают нижним индексом после запятой, как показано в следующих примерах:
изображают нижним индексом после запятой, как показано в следующих примерах:
а) 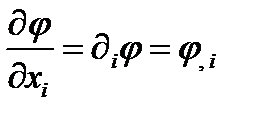 , б)
, б) 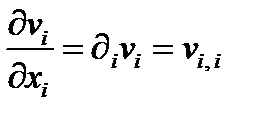 , в)
, в) 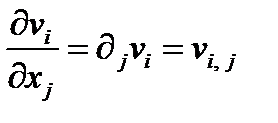 ,
,
г) 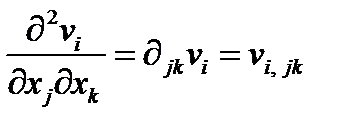 , д)
, д) 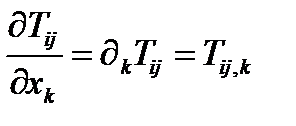 , (257)
, (257)
е) 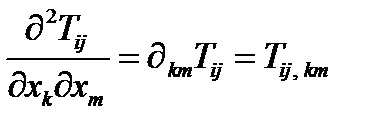
Оператор дифференцирования 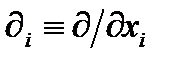 при
при 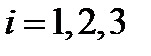 является совокупностью трех операторов
является совокупностью трех операторов 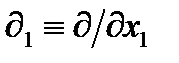 ,
, 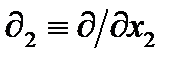 ,
, 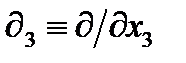 . При переходе к новой системе координат компоненты оператора
. При переходе к новой системе координат компоненты оператора 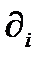 преобразуются как компоненты вектора. В самом деле, в новой координатной системе оператор дифференцирования записывается как
преобразуются как компоненты вектора. В самом деле, в новой координатной системе оператор дифференцирования записывается как 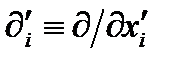 . При этом старые координаты
. При этом старые координаты 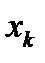 и новые
и новые 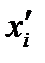 связаны формулами перехода (27), (29):
связаны формулами перехода (27), (29): 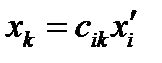 . По правилу дифференцирования сложной функции имеем:
. По правилу дифференцирования сложной функции имеем:
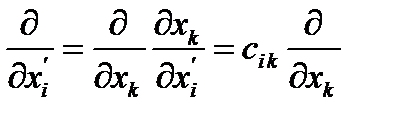 , или
, или 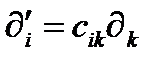 (258)
(258)
В символической бескоординатной записи употребляется известный из курса математического анализа векторный оператор  (набла), который расшифровывается так:
(набла), который расшифровывается так:
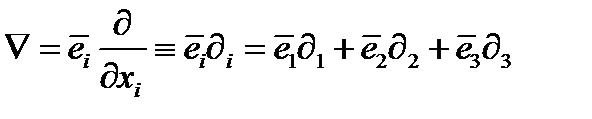 , (259)
, (259)
где 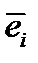 – базисные векторы.
– базисные векторы.
Дифференцирование тензорного поля, т.е. применение оператора 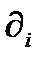 , приводит к тензору на один порядок выше исходного. Покажем это на примере тензорных полей нескольких первых рангов. Дифференцирование скалярного поля
, приводит к тензору на один порядок выше исходного. Покажем это на примере тензорных полей нескольких первых рангов. Дифференцирование скалярного поля 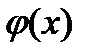 порождает векторное поле
порождает векторное поле 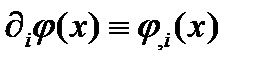 (см. Формулу (257а)). Чтобы доказать это, рассмотрим, как преобразуется
(см. Формулу (257а)). Чтобы доказать это, рассмотрим, как преобразуется 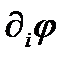 при переходе к новой системе координат. Скаляр
при переходе к новой системе координат. Скаляр 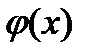 остается инвариантом. Поэтому в новой системе поле будет дифференцироваться так:
остается инвариантом. Поэтому в новой системе поле будет дифференцироваться так:
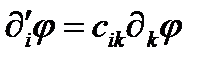 , (260)
, (260)
а это закон преобразования компонент вектора.
Векторное поле 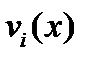 при дифференцировании порождает тензорное поле 2-го ранга
при дифференцировании порождает тензорное поле 2-го ранга 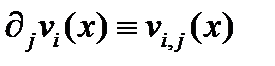 (см. (257в)). В самом деле, в новой координатной системе компоненты векторного поля
(см. (257в)). В самом деле, в новой координатной системе компоненты векторного поля 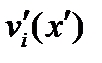 преобразуются по формуле
преобразуются по формуле 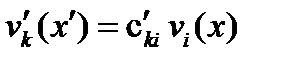 . Поэтому, используя (258), будем иметь:
. Поэтому, используя (258), будем иметь:
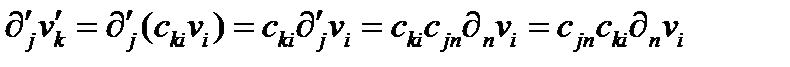 , (261)
, (261)
а это закон преобразования тензора 2-ого ранга.
Наконец, дифференцирование тензорного поля 2-го ранга 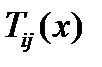 приводит к полю тензора 3-го ранга
приводит к полю тензора 3-го ранга 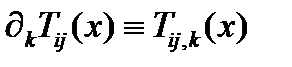 (см. (257д)). В новой системе поле имеет компоненты
(см. (257д)). В новой системе поле имеет компоненты 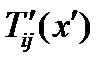 , причем
, причем 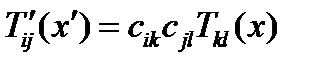 . Применяя (258), получаем:
. Применяя (258), получаем:
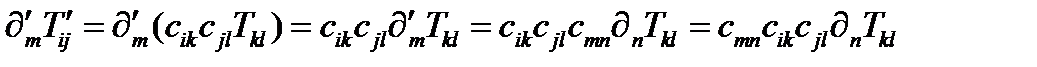 , (262)
, (262)
а это закон преобразования тензора 3-го ранга.
Если при дифференцировании поля производится еще и свертывание по одной паре индексов, как в (257б), то получается тензор ранга на единицу меньше исходного. Повторное дифференцирование без свертывания увеличивает ранг тензора на два (см. (257г,е)).
Для справки приведем некоторые важные дифференциальные операции, изучавшиеся ранее в разделе «Теория поля», в бескоординатной форме и тензорных обозначениях:
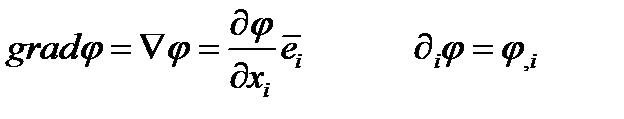 (263а)
(263а)
 (263б)
(263б)
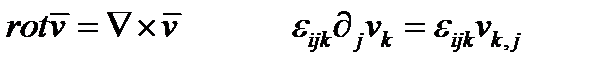 (263в)
(263в)
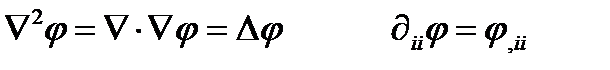 (263г)
(263г)
Операции взятия градиента, дивергенции и ротора распространяются и на тензорные поля более высокого ранга. При этом используется те же символические обозначения, но начинающиеся с заглавных букв. Градиент векторного поля 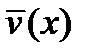 – тензор 2-го ранга, получающийся как внешнее произведение оператора
– тензор 2-го ранга, получающийся как внешнее произведение оператора  на вектор
на вектор 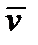 , обозначается:
, обозначается: 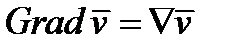 (264)
(264)
Его компоненты равны: 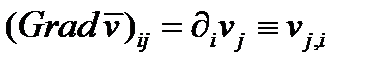 (265)
(265)
След векторного градиента определяет дивергенцию векторного поля (см. (263б)): 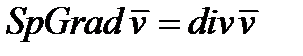 (266)
(266)
Дивергенция тензорного поля 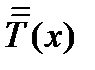 – это вектор, получающийся как скалярное произведение оператора набла на тензор
– это вектор, получающийся как скалярное произведение оператора набла на тензор 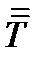 :
:
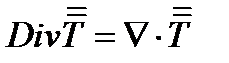 (267)
(267)
Его компоненты: 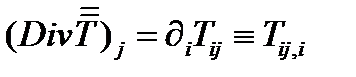 (268)
(268)
Если нужно дифференцировать по второму индексу, то пользуются дивергенцией транспонированного тензора 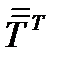 :
:
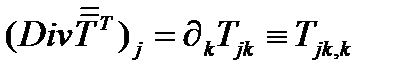 (269)
(269)
Вектор, двойственный векторному градиенту, называется ротором векторного поля (см. (263в)). Ротор тензорного поля 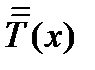 – тензор того же 2-го ранга
– тензор того же 2-го ранга 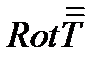 с компонентами:
с компонентами:
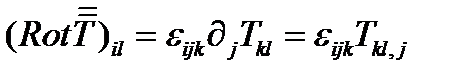 (270)
(270)
Оператор дифференцирования второго порядка 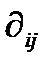 при свертывании определяет известный оператор Лапласа:
при свертывании определяет известный оператор Лапласа:
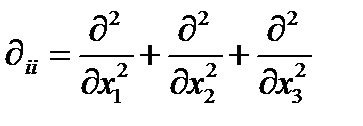 , (271)
, (271)
или в бескоординатной форме:
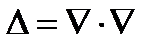 (272)
(272)
Рассмотрим теперь интегрирование в тензорном поле. В курсе математического анализа студенты знакомятся с теоремой Остроградского-Гаусса:
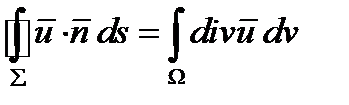 (273)
(273)
Теорема связывает интеграл по замкнутой поверхности 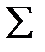 с интегралом по объему
с интегралом по объему  , заключённому внутри этой поверхности,
, заключённому внутри этой поверхности, 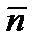 – единичный вектор внешней нормали к поверхности. В тензорных обозначениях теорема записывается так:
– единичный вектор внешней нормали к поверхности. В тензорных обозначениях теорема записывается так:
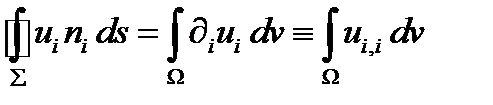 (274)
(274)
Эта теорема допускает обобщение на тензорные поля произвольного ранга. Обобщенная теорема Остроградского-Гаусса выражается равенством:
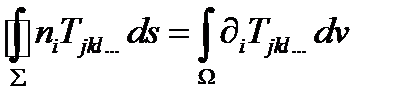 (275)
(275)
Приведем важные частные случаи обобщенной теоремы:
а) Пусть стоящий под знаком интеграла тензор имеет нулевой ранг, т.е. является скаляром 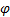 . Тогда:
. Тогда:
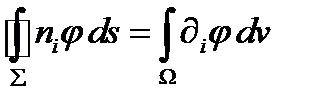 , (276)
, (276)
или в бескоординатной записи:
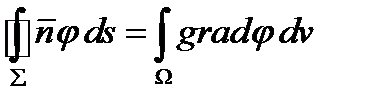 (277)
(277)
б) Векторное поле, т.е. тензор, имеет первый ранг и является вектором 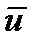 :
:
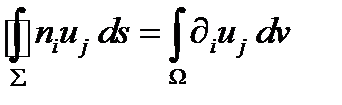 (278)
(278)
Если в этом равенстве произвести свертку по индексам 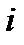 и
и 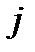 , т.е. приравнять их, и выполнить суммирование, то получим уже известное выражение (274). Если же с помощью
, т.е. приравнять их, и выполнить суммирование, то получим уже известное выражение (274). Если же с помощью 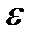 - тензора Леви-Чивиты перейти в (278) к двойственному вектору, то:
- тензора Леви-Чивиты перейти в (278) к двойственному вектору, то:
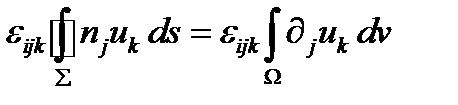 .
.
Внеся ε - тензор под знак интеграла, получаем:
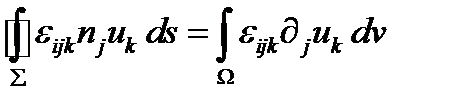 (279)
(279)
В бескоординатной записи это означает:
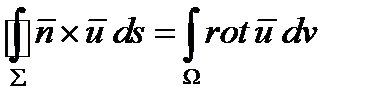 (280)
(280)
в) Тензорное поле второго ранга:
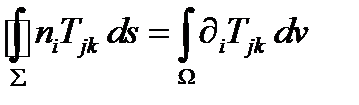 (281)
(281)
Если произвести свертку по индексам 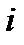 и
и 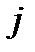 , то:
, то:
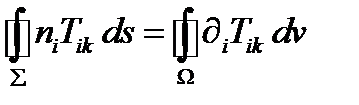 , или (282)
, или (282)
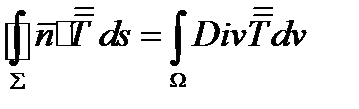 (283)
(283)
Вторая важная теорема теории поля – это теорема Стокса. Напомним ее. Если 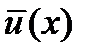 – векторное поле, то криволинейный интеграл от полевого вектора по некоторой кривой
– векторное поле, то криволинейный интеграл от полевого вектора по некоторой кривой 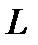
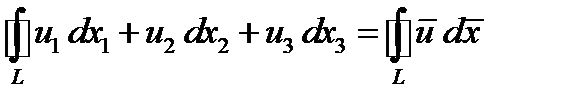 (284)
(284)
называется циркуляцией поля по кривой 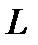 . Теорема Стокса связывает криволинейный интеграл по замкнутому контуру и поверхностный интеграл по любой двусторонней поверхности, «натянутой», на этот контур:
. Теорема Стокса связывает криволинейный интеграл по замкнутому контуру и поверхностный интеграл по любой двусторонней поверхности, «натянутой», на этот контур:
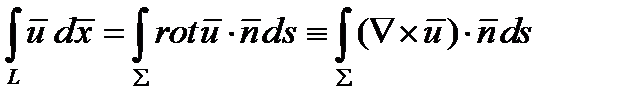 (285)
(285)
В тензорных обозначениях теорема Стокса записывается так:
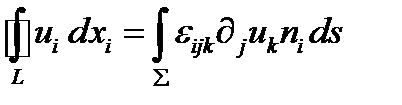 (286)
(286)
Список литературы.
1. Димитриенко Ю.И. Тензорное исчисление – М.: Высшая школа, 2001.– 575 с.
2. Кочин Н.Е. Векторное исчисление и начала тензорного исчисления – М.: Наука, 1965 – 436 с.
3. Прагер В. Введение в механику сплошных сред – М.: ИЛ, 1963. – 311 с.
4. Победря Б.Е. Лекции по тензорному анализу – М.: Издательство МГУ, 1986.– 286 с.
Издание учебное
