Пример разработки программы для решения задачи численного интегрирования в системе Mathcad
Вычисление по квадратурным формулам прямоугольников, трапеций и Симпсона.
Пример.
Найти приближенные значения интеграла  с помощью квадратурных формул прямоугольников, трапеций и Симпсона, если отрезок интегрирования [0;1] разбит на n=2,4,10 равных частей. Оценить величину погрешности полученных результатов в каждом случае.
с помощью квадратурных формул прямоугольников, трапеций и Симпсона, если отрезок интегрирования [0;1] разбит на n=2,4,10 равных частей. Оценить величину погрешности полученных результатов в каждом случае.
Решение
Найдем производные подынтегральной функции до четвертого порядка включительно и максимальные абсолютные значения производных второго и четвертого порядка на отрезке [0;1]:
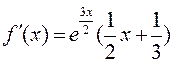



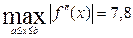
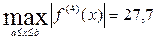
При n=4 получим следующие погрешности результатов:

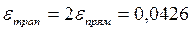

Расчет функции 
 В программном блоке можно читать значения переменных, определенных в MathCAD до этого блока. Однако изменить значения этих переменных внутри программного блока невозможно. Все переменные, которым присваиваются значения внутри программного блока, будут локальными переменными, которые недоступны вне блока. Специально объявлять переменные не нужно, достаточно просто присвоить им значения. Если программный блок является телом функции, то он также может читать значения аргументов этой функции.
В программном блоке можно читать значения переменных, определенных в MathCAD до этого блока. Однако изменить значения этих переменных внутри программного блока невозможно. Все переменные, которым присваиваются значения внутри программного блока, будут локальными переменными, которые недоступны вне блока. Специально объявлять переменные не нужно, достаточно просто присвоить им значения. Если программный блок является телом функции, то он также может читать значения аргументов этой функции.
Программный блок представляет собой группу операторов присваивания и управляющих операторов. Необходимо обратить особое внимание, что все ключевые слова (например, if) в этих операторах обязательно вводятся с помощью панели Programming (Программирование), показанной на рисунке. Их ввод с клавиатуры - ошибка! Открыть панель программирования можно с помощью панели Math,кликнув на кнопке  .
.
В целом правила работы с операторами те же, что и в языке Pascal, отличия касаются способа записи операторов. Разобраться в этом нам поможет таблица1:
Таблица 1. Соответствие программных операторов MathCAD и Pascal
| Оператор языка Pascal | Оператор MathCAD | Комментарий |
| A := B | 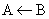 | Присваивание |
| Begin оператор1; оператор2; … End |  | Группа, объединяющая несколько операторов в один составной оператор. Для создания группы и добавления в нее новой пустой строчки используется кнопка «Add Line» панели Programming |
| If условие Then оператор If условие Then Begin оператор1; оператор2; … End | оператор if условие 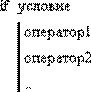 | Простой оператор ветвления. Как и в языке Pascal, его действие распространяется на один указанный оператор, который может быть группой операторов. Условием может быть любое логическое выражение, которое может содержать знаки отношения (вместо обычного знака равенства используется знак логического равенства) и логические операторы (находятся на панели Boolean): 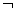 - Not; - Not;  - And; - And;  - Or; - Or; 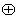 - Xor - Xor |
| If условие Then оператор1 Else оператор2 |  | Полный оператор ветвления |
| For инд := нач To кон Do оператор |  | Фиксированный оператор цикла. Индексная переменная принимает значения от начального до конечного с шагом, равным единице. Цикл действует на один указанный оператор, который может быть группой операторов |
| While условие Do оператор | 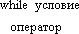 | Гибкий оператор цикла с предусловием. Цикл выполняется, пока истинно заданое условие |
| Нет прямого аналога | выражение1 on error выражение2 | Специальная операция обработки ошибок. Сначала вычисляется выражение2. Если при этом происходит ошибка, то результатом операции будет выражение1. Если ошибки нет, то результат - выражение2. 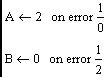 Пример: Здесь локальная переменная A получает значение 2, переменная B - значение 0,5 Пример: Здесь локальная переменная A получает значение 2, переменная B - значение 0,5 |
Если функция является программным блоком, то значение, которое возвращает функция, - это обычно значение, вычисленное последним сработавшим оператором блока. Достоинством MathCAD’а является то, что не следуем заботиться об определении типов переменных – MathCAD осуществляет это сам.
Назовем данную функцию fun(x) и присвоим локальной переменной значение заданной функции:
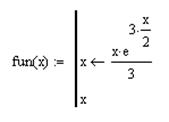
Расчет интеграла по формуле прямоугольников.
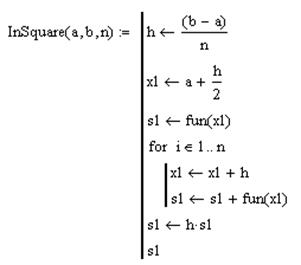
InSguare(0,1,2) = 1.753
Рассчитаем погрешность интегрирования с помощью функции
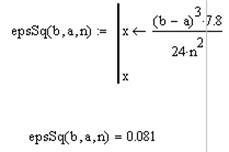
Расчет интеграла по формуле трапеций.
Аналогично, как в предыдущем примере рассчитываем интеграл, с той лишь разницей, что теперь интеграл будет равен сумме элементарных трапеций, площадь которых хранится в переменной х2.
Рассчитаем погрешность с помощью функции:
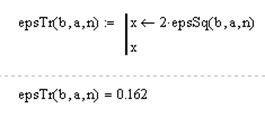

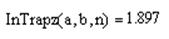
Расчет интеграла по формуле Симпсона.
Рассчитаем интеграл через полученные значения по формулам прямоугольников и трапеций, используя формулу:




Вычисление по формуле Гаусса с тремя узлами
Найти приближенные значения интеграла  по квадратурной формуле Гаусса с тремя узлами для n=2( без разбиения отрезка [0;1] на части, h=1). Сравнить полученный результат с результатами вычислений в предыдущем примере.
по квадратурной формуле Гаусса с тремя узлами для n=2( без разбиения отрезка [0;1] на части, h=1). Сравнить полученный результат с результатами вычислений в предыдущем примере.
Решение
Найдем производные подынтегральной функции до шестого порядка включительно, продолжая вычисления из предыдущего примера:
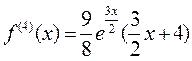
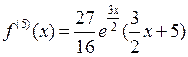
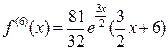


С погрешностью, не большей чем 0,001 имеем
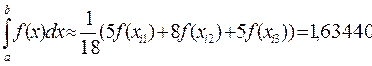 ,
,
x2=0,5; f(x2)=1,41247
 f(x1)=1,46312
f(x1)=1,46312
 f(x3)=2,10203
f(x3)=2,10203
Написание Mathcad-программы для вычисления интеграла по формуле Гаусса комментариев не требует.
Контрольные вопросы
1.Что такое квадратурные формулы?
2.Какие квадратурные формулы вы знаете?
3. Какая из квадратурных формул имеет наименьшую погрешность при одинаковом числе разбиений интервала интегрирования?
4.Что дает метод двойного пересчета?
5. Какая из квадратурных формул имеет меньшую погрешность:
- квадратурная формула прямоугольников
- квадратурная формула трапеций?
Раздел 6
