Тема 1. Случайные события и их классификация. Классическое определение вероятности

Содержание

Тема 1. Случайные события и их классификация. Классическое определение вероятности. 4

Тема 2. Теоремы сложения и умножения вероятностей. Условная вероятность 20

Тема 3. Формула полной вероятности и формула Байеса 31

Тема 4. Схема независимых испытаний Бернулли. Формула Бернулли. Наивероятнейшее число наступлений события.. 46

Тема 5. Формула Пуассона. Локальная и интегральная формулы Муавра - Лапласа 56

Тема 6. Случайные величины... 64

Тема 7. Числовые характеристики случайных величин 83

Тема 8. Основные законы распределения случайных величин 98

Тема 9. Законы распределения двумерной случайной величины 112

Тема 10. Выборка и ее представление. Выборочные моменты 123

Тема 11. Методы нахождения точечных оценок.. 135

Тема 12. Интервальные оценки. Построение доверительных интервалов 140

Тема 13. Задачи проверки статистических гипотез. 143

Список литературы... 160

Приложения.. 161

Тема 1. Случайные события и их классификация. Классическое определение вероятности.

Пусть проводится некоторый опыт (эксперимент, наблюдение, испытание), исход которого предсказать заранее нельзя. Такие эксперименты в теории вероятностей называют случайными. При этом рассматриваются только такие эксперименты, которые можно повторять, хотя бы теоретически, при неизменном комплексе условий произвольное число раз.

Случайным событием (или просто событием) называется любой исход опыта, который может произойти или не произойти. События обозначаются большими латинскими буквами А, В, С,…

Для каждого опыта можно выделить совокупность случайных событий, которые называются элементарными.

Элементарные события – это события, одно и только одно из которых обязательно происходит в результате опыта.

Элементарные события обозначаются .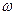

Множество элементарных событий, называемое также пространством элементарных событий, обозначается .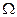

Пример 1. Подбрасывается игральная кость. Элементарные события:

- выпадение единицы,

- выпадение двойки,

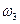- выпадение тройки,

- выпадение четверки,

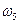- выпадение пятерки,

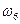- выпадение шестерки.

.

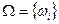В пространстве элементарных событий некоторому событию соответствует некоторое подмножество элементарных исходов. Эти исходы удовлетворяют определенным свойствам, и если реализуется один из этих исходов, то говорят, что наступает событие .

Данное подмножество может содержать один исход, конечное, счетное, несчетное множество исходов, все пространство элементарных событий или ни одного исхода.

Пример 2. Подбрасывается игральная кость. Событие состоит в выпадении четной грани. Оно состоит из трех элементарных исходов - выпадение двойки, - выпадение четверки, и 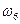- выпадение шестерки.