Выборочные характеристики

К показателям, характеризующим центр распределения, относят различные виды средних (арифметическое, геометрическое и т.п.), а также моду и медиану.

Простейшим показателем, характеризующим центр выборки, является мода.

Мода (М₀) – это такое значение варианты, что предшествующее и следующее за ним значения имеют меньшие частоты встречаемости (наиболее вероятная величина).

Для одномодальных распределений мода – это наиболее часто встречающаяся варианта в данной совокупности.

Например, мода распределения:

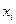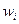равна 18.

Для определения моды интервальных рядов служит формула:

,

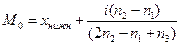где 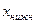– нижняя граница модального класса, т.е. класса с наибольшей частотой встречаемости ;

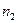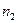– частота модального класса;

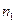– частота класса, предшествующего модальному;

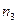– частота класса, следующего за модальным;

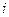- ширина классового интервала.

Медиана 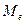– это значение признака, относительно которого ряд распределения делится на две равные по объему части. Иначе говоря, медиана (выборочная медиана) – это число, которое является серединой выборки, т.е. половина чисел имеет значения большие, чем медиана, а половина чисел имеет значения меньшие, чем медиана. Для нахождения медианы обычно выборку ранжируют – располагают элементы в порядке возрастания.

Например, в распределении: 12, 14, 16, 18, 20, 22, 24, 26, 28 медианой будет центральная варианта, т.е. 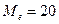,т.к. по обе стороны от нее отстоит по 4 варианты.

Для ряда с четным числом членов: 6, 8, 10, 12, 14, 16, 18, 20, 22, 24 медианой будет полусумма его центральных членов, т.е. .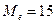

Показателями, характеризующими форму распределения, являются выборочные эксцесс и асимметрия.

Эксцесс – это степень выраженности «хвостов» распределения, т.е. частоты появления удаленных от среднего значений. В качестве показателя эксцесса используется величина 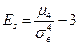. Если 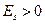,то эксцесс считают положительным (график ряда распределения островершинный), в противном случае – плосковершинный.

Асимметрия – величина, характеризующая несимметричность распределения элементов выборки относительно среднего значения. В качестве показателя асимметрии используется величина 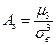, которая называется нормированным моментом третьего порядка. Если 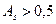(независимо от знака), то асимметрия считается существенной. Асимметрия принимает значения от -1 до 1. В случае симметрического распределения асимметрия равна 0.

Часто значения асимметрии и эксцесса используют для проверки гипотезы о том, что данные (выборка) принадлежат к определенному теоретическому распределению, в частности, нормальному распределению. Для нормального распределения асимметрия равна нулю, а эксцесс – трем.

Выборочные моменты

Начальным выборочным моментом 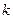- го порядка называется случайная величина

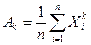
При 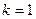начальный выборочный момент является оценкой математического ожидания генеральной совокупности и называется выборочное среднее

.

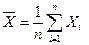Центральным выборочным моментом 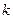- го порядка называется случайная величина

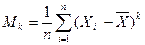
При 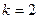центральный выборочный момент является оценкой дисперсии генеральной совокупности и называется выборочной дисперсией

.
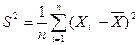