Корреляционный момент и коэффициент корреляции
Определение:
Корреляционным моментом 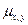 случайных величин
случайных величин  и
и 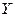 называют математическое ожидание произведения отклонений этих величин
называют математическое ожидание произведения отклонений этих величин
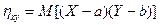
Напомним, что приведенное выражение является элементом формулы дисперсии суммы двух случайных величин:

Замечание:
Корреляционный момент 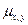 может быть представлен в виде:
может быть представлен в виде:

Доказательство:

Теорема:
Корреляционный момент двух независимых случайных величин  и
и 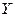 равен 0
равен 0
Доказательство:
Согласно замечанию:
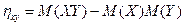
Но для независимых случайных величин

Тогда для независимых случайных величин  и
и 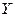 :
:

Определение:
Безразмерная величина 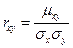 называется коэффициентом корреляции.
называется коэффициентом корреляции.
Теорема:
Абсолютная величина корреляционного момента двух случайных величин не превосходит произведения их средних квадратических отклонений:

Доказательство:
Введем в рассмотрение случайную величину  и найдем ее дисперсию:
и найдем ее дисперсию:
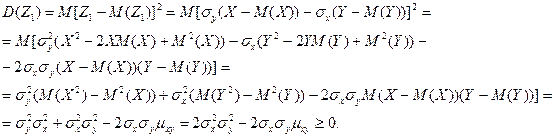
Или
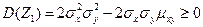 , так как любая дисперсия неотрицательная
, так как любая дисперсия неотрицательная
Отсюда
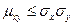 .
.
Аналогично введем случайную величину 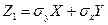 и найдем, что:
и найдем, что:
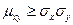 .
.
Или
 .
.
Определение:
Случайные величины  и
и 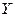 называются некоррелированными, если
называются некоррелированными, если  , и коррелированными, если
, и коррелированными, если  .
.
Теорема:
Коэффициент корреляции случайных величин, связанных линейной зависимостью, равен 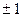 .
.
Доказательство:
Пусть
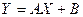 ;
; 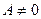
Найдем коэффициент корреляции:


Откуда
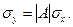
и
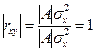
Отметим некоторые свойства коэффициента корреляции.
1. Из примера 1 следует, что если 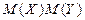 - независимые случайные величины, то коэффициент корреляции равен 0.
- независимые случайные величины, то коэффициент корреляции равен 0.
Заметим, что обратное утверждение неверно.[40]
2. Абсолютная величина коэффициента корреляции в общем случае не превосходит единицы:

Доказательство следует из доказанной ранее формулы для корреляционного момента:
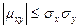
Разделим обе части неравенства на произведение 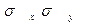 и получим
и получим 
3. Коэффициент корреляции характеризует относительную (в долях 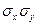 ) величину отклонения математического ожидания произведения
) величину отклонения математического ожидания произведения  от произведения математических ожиданий
от произведения математических ожиданий 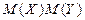 величин
величин 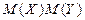 . Так как такое отклонение имеет место только для зависимых величин, то можно сказать, что коэффициент корреляции характеризует тесноту зависимости между
. Так как такое отклонение имеет место только для зависимых величин, то можно сказать, что коэффициент корреляции характеризует тесноту зависимости между  и
и 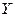 .
.
Это утверждение следует из доказанного ранее равенства: 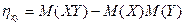 . Приведем корреляционный момент к коэффициенту корреляции:
. Приведем корреляционный момент к коэффициенту корреляции:
 .
.
[1] Куликов А. А. Форекс для начинающих. Справочник биржевого спекулянта – СПб.: Питер, 2007; Коммерсантъ № 62 от 13.04.2007 – Мировая торговля замедлится.
[2] Bachelier L. Theorie de la speculation. //Annales de l'Ecole Normale Superieure. 1900. V. 17. P. 21-86. Описание идей Л. Бушелье, их судьба и их современная критика содержатся в книгах: Мандельброт Б. Непослушные рынке, фрактальная революция в финансах – пер. с англ. – М.: Издательский дом «Вильямс», 2006; Сорнетте Д. Как предсказывать крахи финансовых рынков – пер. с франц. – М.: Издательство «И-трейд», 2008.
[3] Cootner Paul H. The Random Character of Stock Market Prices – Cambridge, MA, MIT Press
[4] Harry M. Markowitz, Portfolio Selection, Journal of Finance, 7, no 1 (March 1952), pp, 79-81.
[5] В представленном разделе используются материалы следующих книг: Шарп У. Ф.., Александер Г. Дж., Бэйли Дж. В. Инвестиции – пер. с англ. – М.: ИНФРА-М, 1997; Бромвич М. Анализ экономической эффективности капиталовложений – пер. с англ. – М.: ИНФРА-М, 1996; Ширяев В. И. Модели финансовых рынков. Оптимальные портфели, управление финансами и рисками – Учебное пособие – М.: КомКнига, 2007; Шаповал А. Б. Инвестиции: математические методы – М.: ФОРУМ: ИНФРА-М, 2007; Коростелева М. В. Методы анализа рынка капитала – СПб.: Питер, 2003.
[6] Тобин Дж. обратил внимание на недостаточность показателей математических ожиданий и дисперсии для сравнения портфелей (См. Ширяев В. И. Модели финансовых рынков… - стр. 18-19). Тем не менее, их применение оправдано своей конструктивностью.
[7] См. Аскинадзи В. М. и др. Инвестиционное дело – Учебник - М.: Маркет ДС, 2007, стр. 238-241 или Ширяев В. И. Модели финансовых рынков. Оптимальные портфели, управление финансами и рисками – Учебное пособие – М.: КомКнига, 2007, стр. 17.
[8] См. Бромвич М. Анализ экономической эффективности капиталовложений – пер. с англ. – М.: ИНФРА-М, 1996, стр. 343. Обсуждение альтернативных мер риска, например, приведение к нормальному типу так называемого логнормального распределения можно найти в книге: Шарп У. Ф.., Александер Г. Дж., Бэйли Дж. В. Инвестиции – пер. с англ. – М.: ИНФРА-М, 1997, стр. 179-181.
[9] См. Бромвич М. Ук. Соч. стр. 342.
[10] Считают, что первым шагом в создании теории полезности было формулирование так называемого Санкт-Петербургского парадокса. Любопытно, что сформулировал этот парадокс Николай Бернулли, а объяснение дал ему Даниил Бернулли - См.: Бернулли Д. Опыт новой теории измерения жребия / Д. Бернулли; пер. А. Нардовой // Вехи экономической мысли / сост. и общ. ред. В. М. Гальперина. Спб., 1993. Т. 1 : Теория потребительского поведения и спроса. С. 11-27.
Полезные материалы по теории полезности можно найти в книгах, посвященных теории игр, в частности: Льюс Р.Д., Райфа Х. Игры и решения - Пер. с англ. - М.: Изд-во иностр. лит., 1961; Нейман фон Джон, Моргенштерн О. Теория игр и экономическое поведение - Пер. с англ. - М.: Наука, 1970.
[11] См. Приложение к модели Г. Марковица
[12] См. в книге Ширяева В. И. Модели финансовых рынков. Оптимальные портфели, управление финансами и рисками – М.: КомКнига, 2007, стр. 25-26.
[13] Аналитическую формулировку модели Марковица можно найти в книгах: Шаповал А. Б. Инвестиции: математические методы – М.: ФОРУМ: ИНФРА-М, 2007, стр. 21-22; Аскинадзи В. М. и др. Инвестиционное дело – Учебник - М.: Маркет ДС, 2007, стр. 288.
[14] Нами использованна формулировка, предложенная в книге: Аскинадзи В. М. и др. Инвестиционное дело – Учебник - М.: Маркет ДС, 2007, стр. 256-257.
[15] См. в книге: Шаповал А. Б. Инвестиции: математические методы – М.: ФОРУМ: ИНФРА-М, 2007, стр. 16-18 (раздел «Модель Марковица»).
[16] См.:Шарп У. Ук. соч. стр. 213-218, 226-228, стр. 271 – о связи и отличиях рыночной модели и модели САРМ; также Аскинадзи В. М. и др. Ук. соч., стр. 278-294; Ширяев В. В. Ук. соч., стр. 47-58
[17] См.: Шарп У. Ф., Александер Г. Дж., Бэйли Дж. В. Инвестиции –пер. с англ. – М.: ИНФРА-М, 1997, стр 316-337.
[18] См.: Оценка бизнеса – под ред. Грязновой А.Г., Федотовой М.А. – М.: Финансы и статистика, 2007, стр. 199
[19] См: Шаповал А. Б. Инвестиции: математические методы – М.: ФОРУМ: ИНФРА-М, 2007, глава 3.
[20] См. Мандельброт Б., Хадсон Р. Л. Непослушные рынки: фрактальная революция в финансах – пер. с англ. – М.: Издательский дом «Вильямс», 2006, 187 стр.
[21] См. там же, стр. 34-39.
[22] См.: Сорнетте Д. Как предсказывать крахи финансовых рынков – пер. с франц. – М.: Издательство «И-трейд», 2008, стр. 19-22.
[23] Это раздел основан, главным образом, на материалах книги: Экономическая теория (New Palgraiv) – пер. с англ. – М.: ИНФРА-М, 2004, стр. 263-273 – глава Гипотеза эффективного рынка, автор - Бертон Мэлкил (Berton G, Malkiel). Ссылки на авторов различных исследований также сделаны по материалам этой статьи. См. также: Бертон Мэлкил «Случайная прогулка по Уолл-Стрит – пер. с англ. - Минск: Попурри, 2006. Последняя книга издается уже 30 лет. Любопытно, что в конце 90-х годов вышла иная книга: Эндрю Лоу. Неслучайная прогулка по Уолл-Стрит. Б. Мелкил является, в целом, сторонником гипотезы эффективного рынка, а Эндрю Лоу – наоборот.
[24] См.: Чеботарев Ю.Н. Случайность и Неслучайность биржевых цен – М.: СмартБук; И-трейд, 2008, 198.
[25] Инвариантность - неизменность какой-либо величины при изменении физических условий или по отношению к некоторым преобразованиям, например, преобразованиям координат и времени при переходе от одной инерциальной системы отсчета к другой (релятивистская инвариантность). Практически строгое описание «случайного блуждания» в наиболее простой версии «винеровского процесса» можно найти в книге: Шаповал А.Б. Инвестиции: математические методы – Учебное пособие – М.: ФОРУМ: ИНФРА-М, 2007, стр. 42-43.
Случайный процесс называется винеровским, если выполнены следующие условия:
1) Процесс начинается с нуля, то есть ;
2) Случайная величина имеет нормальное распределение с нулевым математическим ожиданием и с дисперсией равной для любого момента времени ;
3) Для произвольных непересекающихся интервалов и случайные величины и независимы.
Вообще, пособие Шаповала А.Б. мы рекомендуем для ознакомления с математическими моделями портфельного анализа, оценки опционов. Изложение достаточно строгое для практики и краткое (96 стр.), но вводит в современную теорию финансов. В главе о портфельном анализе мы в значительной мере используем
[26] См. материал из Википедии:
Последовательность случайных величин называется мартингалов с дискретным временем, если:
, ;
,
Пусть дана другая последовательность случайных величин . Тогда последовательность случайных величин называется мартингалом относительно или -мартингалом, если:
,
, .
Пусть дана последовательность случайных величин . Тогда последовательность случайных величин называется суб(супер) мартингалом относительно , если:
,
, .
[27] Этот эффект можно объяснить налоговым влиянием. В конце года инвесторы сбрасывают акции, в первую очередь, мелких фирм для имитации убыточности и облегчения налоговых платежей, цены акций падают, а в январе они могут вернуться даже с излишком вверх – См.: Бертон Мэлкил. Случайная прогулка по Уолл-Стрит, стр. 316-317.
[28] Эффект уик-энда, эффект понедельника не имеет однозначного объяснения. Эффект говорит о том, что цены акций в понедельник ниже, чем вечером в пятницу. В книге «Случайная прогулка по Уолл-Стрит» Бертон Мэлкил уточняет эффект: цены акций утром в понедельник немного выше, чем вечером в пятницу, а к вечеру понедельника они понижаются, так что доходность становится относительно отрицательной. Поэтому следует покупать акции в понедельник вечером. Но проверка эффекта, проведенная автором по материалам Нью-Йоркской фондовой биржи с мая по июль 2002 года показала, что эффект проявился лишь в восьми уик-эндах из тринадцати.
Можно рекомендовать также материал:Б. Френкель, Д. Альберг. Симуляционный подход к объяснению эффекта конца недели на адресе:ttp://www.tsi.lv/journal_T&T/Transport&Telecommunication/v52_ru/4_rus.pdf
[29] Стратегию «купил и держи» реализуют так называемые «индексные фонды», которые держат структуру своих вложений в соответствии с популярными биржевыми индексами. По данным информационного портала «Вложи.ру», в России в 2007 году действовало 11 ПИФов как индексные фонды. Первый российский индексный фонд был образован в 2003 году. В США такие фонды действуют уже 30 лет. Российские фонды ориентируются на индексы ММВБ или РТС (после модификации в 2006 году индекс РТС стал учитывать и ликвидность бумаг, что требуется для правильной работы индексного фонда). Строго следовать индексам индексные фонды, конечно, не могут, так как было бы нерационально вносить изменения во вложения непрерывно. См. материалы об индексных фондах на портале частного инвестора «Вложи.ру»: http://www.vlozhi.ru/
[30]Дробление акций снижает их номинальную стоимость, в результате чего она становится более доступной мелким акционерам. Расширение рынка акций может повысить к ним интерес и, соответственно, увеличить спрос на них, а значит, и рыночную стоимость акций
[31] Эффективность взаимных фондов относительно эффективности индексных акций за 1980-1990 годы см.: Бертон Мэлкил. Случайная прогулка по Уолл-Стрит, стр. 238. В 80-е годы взаимные фонды обгоняли индекс S&P 500, в 90-е годы – отставали. Там же и другие современные материалы по эффективности взаимных фондов. Например, по данным с 1968 по 2002 годы проведено сопоставление доли наличности в активах взаимных фондов и индекса S&P 500. Сопоставление показало, что доля наличности в активах фондов была высока именно в те моменты, когда индекс был низок, то есть когда надо было, наоборот, тратить наличные деньги на покупку акций – стр. 244-248.
[32] Результаты расчетов см.: Бертон Мэлкил. Случайная прогулка по Уолл-Стрит, стр. 235.
[33] См. номера журнала «Финанс» за 2009-2010 годы.
[34] См. Элдер А. Как играть и выигрывать на бирже: Психология. Технический анализ. Контроль над капиталом – М.: Альпина Бизнес Бук, 2007, стр. 29-35.
[35] См.: Дамодаран А. Инвестиционные байки: разоблачение мифов о безпроигрышных биржевых стратегиях – пер. с англ. СПб.: Питер, 2007, стр. 396-428.
[36] См.: Хэгстром Р. Дж. Инвестирование. Последнее свободное искусство – пер. с англ. – М.: ЗАО «Олимп-Бизнес», 2005.
[37] Сравнение среднегодовой доходности и риска (квадратичного отклонения доходности) акций компаний крупных и мелких за период с 1926-2001 показало, что среднегодовая доходность акций мелких компаний – 17.5%, а крупных – 12.4 при риске 35.3 и 20.8%% соответственно. Среднеожидаемый ежемесячный доход за период 1963-1990 годы также показывает зависимость от размера компании. В то же время в 90-е годы ситуация изменилась, большие доходы стали давать компании с высокой капитализацией. Дело, по-видимому, в том, что выросла доля институциональных инвесторов, работающих с акциями крупных компаний, и акции мелкий компаний потеряли часть ликвидности – См. Бертон Мэлкил. Случайная прогулка по Уолл-Стрит, стр. 265, 333-334.
[38] Данные за 80-е годы показывают, что акции с низким коэффициентом доходности (отношение цены акции к чистой прибыли компании) показывали более высокую доходность. Аналогично, акции с низким оотношением цены к стоимости активов фирмы дают обычно большую доходность – См. Бертон Мэлкил. Случайная прогулка по Уолл-Стрит, стр. 334-340.
[39] Доказательства приведены по материалам книги: Бромвич Майкл. Анализ экономической эффективности капиталовложений – М.: ИНФРА-М, 1996.
[40] См. Б.В. Гнеденко. Курс теории вероятности – М.: Наука, 1969, стр. 179 (глава 5. Числовые характеристики случайных величин)
