Инверсный фильтр Чебышева

Методические указания

к лабораторной работе по теме:

«Построение цифрового фильтра с заданной структурой»

Пермь 2015

СОДЕРЖАНИЕ

1.ЦЕЛЬ РАБОТЫ................................................................................................................... 3

1.1. Требования к выполнению задания.................................................................................. 3

2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ........................................................... 4

2.1. Обзор КИХ-фильтров......................................................................................................... 8

2.2. Обзор БИХ-фильтров......................................................................................................... 9

2.3. Нелинейный медианный фильтр...................................................................................... 9

3. РЕАЛИЗАЦИЯ LABVIEW..................................................................... 10

3.1. Фильтр Баттерворта.......................................................................................................... 11

3.2. Фильтр Чебышева............................................................................................................. 15

3.3. Инверсный фильтр Чебышева......................................................................................... 16

3.4.Эллиптический фильтр..................................................................................................... 18

3.5. Фильтр Бесселя.................................................................................................................. 20

3.6. Фильтр нижних частот с равномерными пульсациями................................................ 22

3.7. Фильтр верхних частот с равномерными пульсациями............................................... 24

3.8. Полосовой фильтр с равномерными пульсациями....................................................... 24

3.9. Режекторный фильтр с равномерными пульсациями................................................... 25

3.10. Оконный КИХ-фильтр................................................................................................... 25

3.11. Медианный фильтр......................................................................................................... 28

3.12. Инверсный f-фильтр....................................................................................................... 30

3.13. Фильтр с нулевым смещением фазы............................................................................. 32

4. ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ.......................... 35

4.1. Пример выполнения задания........................................................................................... 35

4.2. Варианты заданий............................................................................................................. 40

4.3. Содержание отчета........................................................................................................... 41

4.4. Контрольные вопросы...................................................................................................... 41

5. СПИСОК ЛИТЕРАТУРЫ...................................................................... 42

1. ЦЕЛЬ РАБОТЫ

Изучить теоретические сведения о цифровой фильтрации; выполнить фильтрацию измеренного датчиком сигнала; оценить точность (ошибку) фильтрации.

1.1. Требования к выполнению задания:

1. Написать программу, реализующую фильтрацию сигналов

2. Предусмотреть визуализацию сигналов

3. Описать основные алгоритмы программы.

4. Оформить отчет.

2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Общее соотношение между процессами x(t) на входе и y(t) на выходе линейного фильтра дается интегралом свертки вида

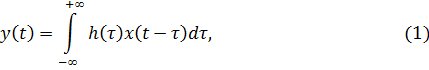
где 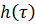– весовая функция фильтра.

Интеграл в интегральном уравнении (1) есть свертка функций 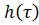и x(t). Частотная характеристика фильтра представляет собой преобразование Фурье (F-преобразование) функции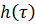

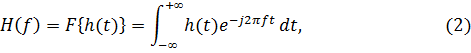
где f – частота, Гц.

Если h(t) = 0 при t < 0, то соотношение (2) примет вид

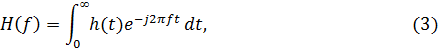
где 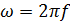– угловая частота, рад.

Обратное преобразование Фурье ( 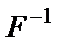-преобразование) позволяет получить функцию h(t) из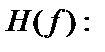

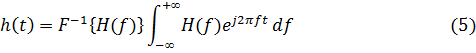
или

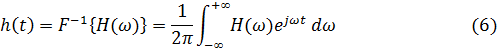
При построении цифрового фильтра в противоположность аналоговому случаю нет необходимости вводить условие физической осуществимости. Иначе говоря, не нужно требовать, чтобы весовая функция была равна нулю при t < 0, поскольку данные могут быть накоплены в ЭВМ и в нужный момент поданы на фильтр для фильтрации их в обратном порядке.

Идеальным фильтром можно считать систему, имеющую одну полосу пропускания или более (ряд частот, для которых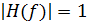
и одну полосу непрозрачности или более (ряд частот, для которых 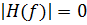)). Простые идеальные фильтры обычно подразделяют
на фильтры нижних и верхних частот и полосовые. Примеры идеальных амплитудно-частотных характеристик 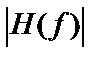низкочастотного, высокочастотного и полосового фильтров даны на рис. 1-3, где f0 – частота среза или граничная частота первых двух фильтров; f1, f2 – частоты среза (граничные частоты) полосового фильтра. Примерный вид реальных амплитудно-частотных характеристик 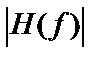низкочастотного, высокочастотного и полосового фильтров показан на рисунках 4-6 соответственно.

Идеальные АЧХ НЧ, ВЧ и полосового фильтров:

|H(f)|

f

f0

|H(f)|

f

f0

|H(f)|

f

f1

Рис. 1 ииИиРеальная АЧХ НЧ фильтра Реальная АЧХ НЧ фильтра

Рис. 2

Рис. 3

f2

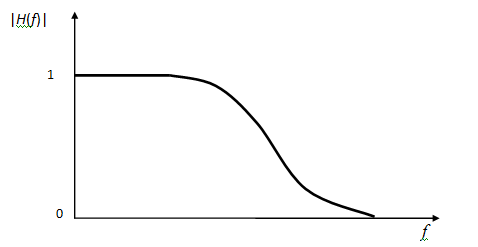
Реальные АЧХ НЧ, ВЧ и полосового фильтров:

Рис. 4 Реальная АЧХ НЧ фильтра Рис. 5 Реальная АЧХ ВЧ фильтра

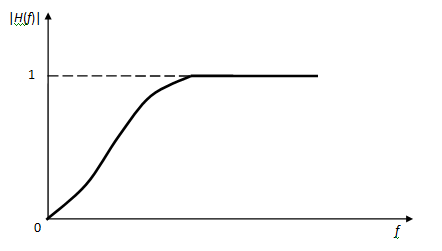
|H(f)|

f

Рис. 6 Реальная АЧХ полосового фильтра

В зависимости от частотного диапазона, который фильтры либо пропускают, либо ослабляют, они могут быть классифицированы на следующие типы:

Низкочастотный фильтр – пропускает низкие частоты, но ослабляет высокие.

Высокочастотный фильтр – пропускает высокие частоты, но ослабляет низкие.

Полосовой фильтр – пропускает определенную полосу частот.

Заграждающий фильтр – ослабляет определенную полосу частот.

Частотные характеристики перечисленных фильтров:

1) Импульсная характеристика ЦФ h[k] – это его отклик на единичный импульс, т.е.сигнал, заданный последовательностью: x[0]=1 и x[i]=0 при i ≠ 0.

2) ДПФ от импульсной характеристики есть частотная характеристика или коэффициент передачи фильтра H[n]:

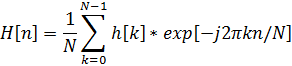
3) По виду импульсной характеристики ЦФ делятся на две группы: КИХ- фильтры (FIRfilters) - фильтры с импульсной характеристикой, имеющей конечную длительность, и БИХ-фильтры (IIR-filters), у которых импульсная характеристика длится бесконечно БИХ-фильтры (IIR-filters), у которых импульсная характеристика длится бесконечно долго

4) По аналогии с линейным аналоговым фильтром, который описывается линейным дифференциальным уравнением с постоянными коэффициентами, цифровой фильтр описывается линейным уравнением в конечных разностях:

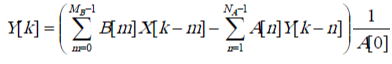
Здесь: X[ n] и Y[k] - входная и выходная последовательности (сигналы); B[m] – «прямые» коэффициенты (Forward Coefficients); A[n] – «обратные» коэффициенты (Reverse Coefficients).

Если все A[n]=0 получим КИХ-фильтр, – фильтр с конечной импульсная характеристикой если A[n] ≠ 0 – БИХ-фильтр, фильтр с – бесконечная импульсная характеристика.

2.1. Обзор КИХ-фильтров

КИХ – фильтры представлены набором из 4-х ВП, каждый из которых реализует один из 4-х перечисленых выше типов фильтров с одинаковым уровнем неравномерности в полосах пропускания и режекции: Equi-Ripple LowPass.vi … Equi-Ripple BandStop.vi. Отдельный ВП FIR Widowed Filter.vi является универсальным и в зависимости от значения входа filter type позволяет реализовать любой тип фильтра. Значение входа «Отводы» (Taps) должно быть четным для высокочастотных и заграждающих фильтров, так как если оно четное, то амплитудная характеристика стремится к нулю при приближении значения частоты к половинному значению частоты дискретизации. Чем больше эта величина, тем длиннее импульсная характеристика фильтра и, соответственно, дольше длится переходный процесс (тем больше задержка появления сигнала на выходе фильтра). Приведенный ниже пример позволяет познакомиться с характеристиками универсального КИХ-фильтра. Комментарии: 1) значение f вч влияет на работу ВП только для полосовых фильтров (пропускающего и заграждающего) и определяет верхнюю частоту полосы; 2) ошибка отличается от нуля, если задано сочетание параметров, при котором невозможен синтеза фильтра; 3) обратите внимание, что ФЧХ фильтров всегда линейна; 4) для получения непрерывной зависимости фазы от частоты использован ВП Unwrap Phase.vi; 5) для получения на выходе фильтра импульсной характеристики на его вход подается одиночный импульс, генерируемый ВП Impuls Pattern.vi; 6) частотная характеристика вычисляется как БПФ от импульсной.

2.2. Обзор БИХ-фильтров

Первый ряд палитры Signal Processing®Filters содержит набор ВП БИХ-фильтрации различных видов (см. таблицу ниже). Тип фильтра выбирается соответствующим элементом управления. Не рекомендуется выбирать порядок БИХ-фильтров больше 20, т.к. это может привести к неустойчивости.

2.3. Нелинейный медианный фильтр (Signal Processing>Filters)

Наряду с линейными фильтрами, в LabVIEW включен т.н. «медианный фильтр» (Median Filter.vi). Его основное назначение – устранять из сигналов импульсные помехи. При этом такой фильтр практически без искажений пропускает «ступеньку». Это свойство делает его 2-мерный вариант незаменимым при очистке изображений от коротких импульсных помех. Контуры элементов изображения при этом не размываются. Применение традиционного ФНЧ привело бы к расплыванию изображения.

3. РЕАЛИЗАЦИЯ LABVIEW

Виды фильтров наиболее часто применяющихся на практике, также их основные характеристики:

■ фильтры Баттерворта характеризуются гладкостью частотной характеристики на всех частотах. Они имеют наиболее плоскую характеристику в полосе пропускания и ноль в полосе заграждения;

■ фильтры Чебышева имеют малую амплитуду ошибки в полосе пропускания, большую крутизну спада в переходной полосе (по сравнению с фильтрами Баттерворта), плоскую характеристику в полосе заграждения, а так же характеризуются наличием выброса перед переходной полосой;

■ инверсные фильтры Чебышева имеют малую амплитуду ошибки в полосе заграждения и наиболее плоскую характеристику в полосе пропускания.

■ эллиптические фильтры характеризуются самой высокой крутизной в переходной полосе.

Существуют и другие цифровые фильтры. Они также представлены в LabView. Их можно найти в панеле Functions ® Signal Processing ® Filters.

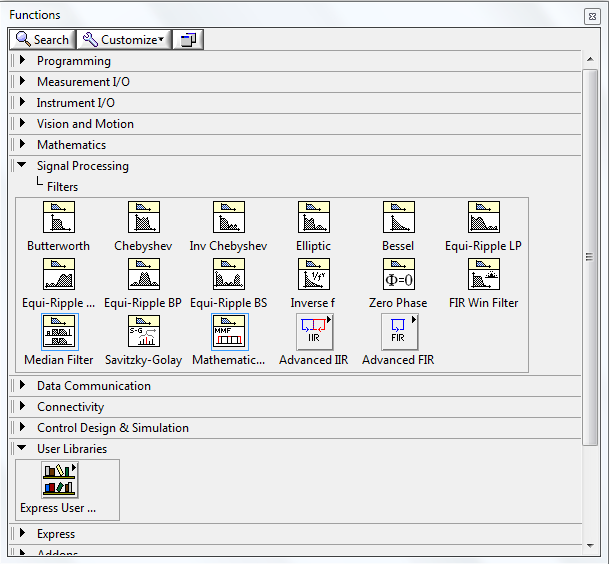
Рис. 7 Панель Functions

3.1. Фильтр Баттерворта

Амплитудно-частотная характеристика 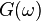фильтра Баттерворта 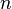-го порядка:

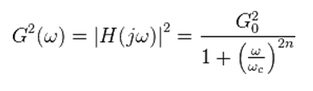
Амплитудно-частотная характеристика:

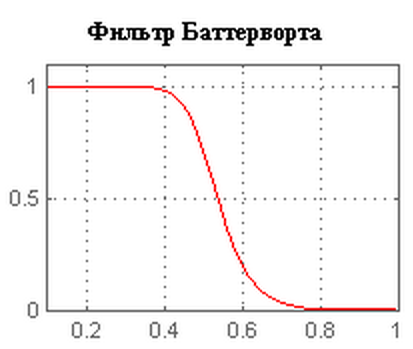
Создадим этот и фильтр и рассмотри его входы, за что каждый из них отвечает.

1) Найдем в Filters фильтр Баттерворта (Butterworth).

Так он выглядит

2) Добавим входы. Для этого необходима катушка (Connector Wire) в панели Tools. Если этой панели нет, то выведем ее на экран через View ® Tools Palette. При наведении катушки на фильтр высвечиваются входы. Они все подписаны.

Например, добавим “filter type”. Наведем катушкой на данный вход и нажмем правой клавишей мышки на него. Create ® Control.

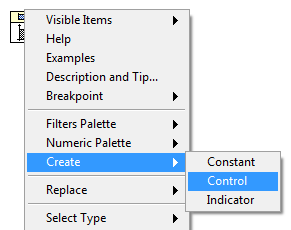
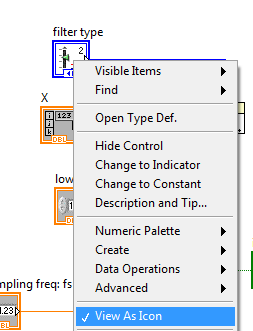
Рис. 8 Создание выходов фильтра

Создадим таким образом входы: входной массив (X); частоту дискретизации (sampling freq); верхняя частоту среза (high cutoff freq), нижнюю частоту среза (low cutoff freq), порядок фильтра (order), «Сбросить/Продолжить» (init/cont).

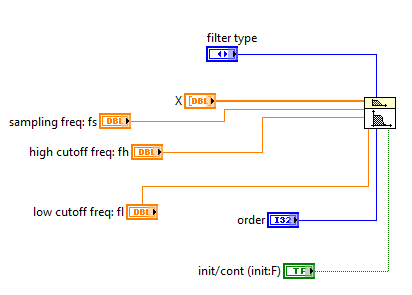
Рис.9 Выходы фильтра Баттерворта (Butterworth).

3) Создадим оставшиеся 2 выхода: «ошибка» (error) и отфильтрованный массив (Filtered X).

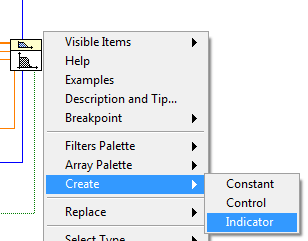
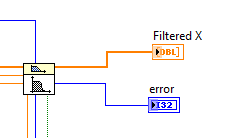
Рис.10 Создание индикатора

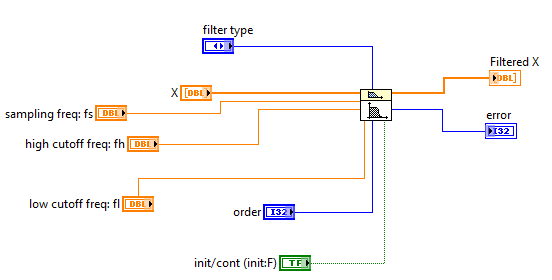
Рис. 11 Фильтр Баттерворта с выходами

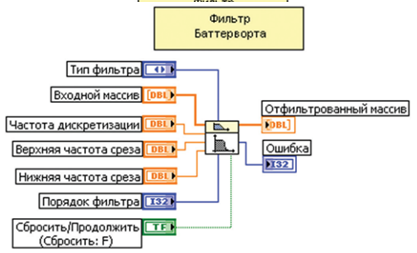
Рис. 12 Фильтр Баттерворта с выходами

Частота дискретизации (sampling freq) определяет количество выборок в секунду. Частота дискретизации не может быть меньше 0, значение по умолчанию - 1.

Верхняя частота среза (high cutoff freq) использу­ется только для полосовых и режекторных фильтров. Верхняя частота среза должна быть больше нижней, а так­же отвечать условию Найквиста, значение по умолчанию - 0,45. Для фильтров верхних и нижних частот данный вход игнорируется.

Нижняя частота среза (low cutoff freq) использует­ся для всех типов фильтров, по умолчанию равна 0,125.

Порядок фильтра (order) устанавливает порядок фильтра, который обязатель­но должен быть боль­ше 0. По умолчанию устанавли­вается вто­рой поря­док фильт­ра.

«Сбросить/Продолжить» (init/cont) управля­ет инициализацией внутренних состояний фильтра. Если на входе значение "FALSE" - внутренние состояния сбрасы­ваются в 0. При установке на этот вход значения "TRUE" - текущие внутренние состояния фильтра будут равны сос­тояниям, установленным во время предыдущего исполь­зования этого VI.

Фильтр Чебышева

Амплитудно-частотная характеристика такого фильтра 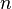-го порядка задаётся следующим выражением:

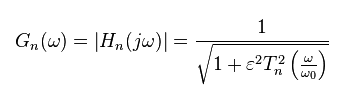
где — показатель пульсаций, 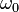— частота среза, а 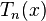— многочлен Чебышёва 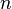-го порядка.

Амплитудно-частотная характреристика :

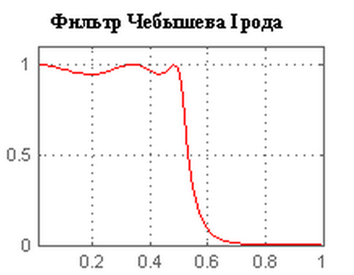
Этот VI имеет такие же входы и выходы, как и рас­смотренный выше фильтр Баттерворта, за исключением входа Пульсации (ripple).

Фильтр Чебышева (Chebyshev)

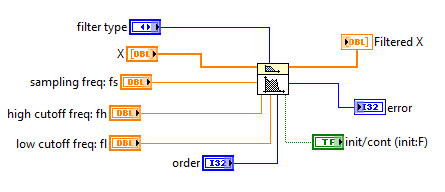
Рис. 13 Фильтр Чебышева с выходами

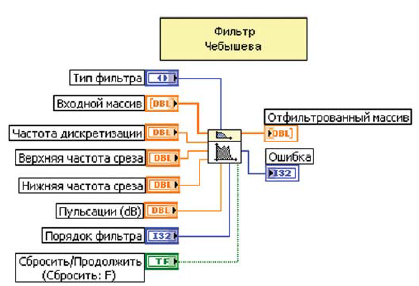
Рис. 14 Фильтр Чебышева с выходами

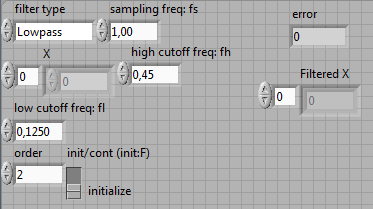
Рис. 15 Панель управления фильтра Чебышева

Фильтры Чебышёва обычно используются там, где требуется с помощью фильтра небольшого порядка обеспечить требуемые характеристики АЧХ.

Инверсный фильтр Чебышева

Амплитудная характеристика такого фильтра задаётся следующим выражением: .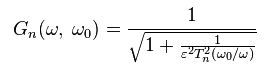

Амплитудно-частотная характреристика:

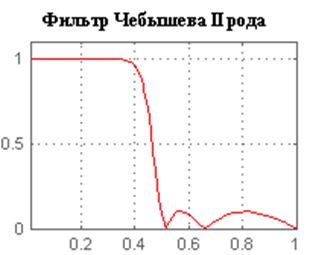
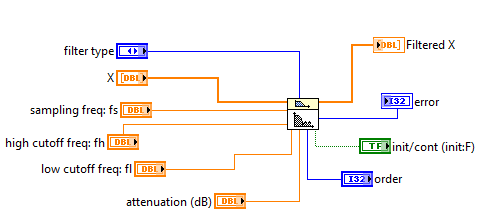
Рис. 16 Инверсный фильтр Чебышева с выходами (Inv Chebyshev)

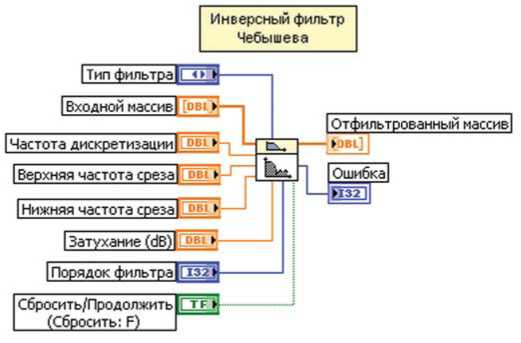
Рис. 17 Инверсный фильтр Чебышева с выходами (Inv Chebyshev)

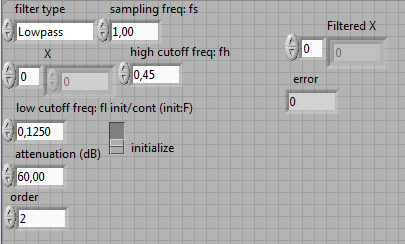
Рис. 18 Панель управления инверсного фильтра Чебышева

Этот тип VI отличается от рассмотренного тем, что вместо входа Пульсации присутствует вход Затухание (attenuation). Значение затухания должно быть больше нуля и зада­ваться в дБ, по умолчанию - 60.

Эллиптический фильтр

Эллиптический фильтр является своего рода объе­динением инверсного и обычного фильтров Чебышева. Благодаря входу Пульсации в полосе пропускания (pass- band ripple), Вы управляете величиной выбросов в облас­ти пропускания, а вход Затухание в полосе заграждения (stopband attenuation) отвечает за ослабление в области заграждения.

Амплитудно-частотная характеристика эллиптического фильтра низких частот:

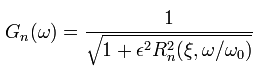
Амплитудно-частотная характреристика:

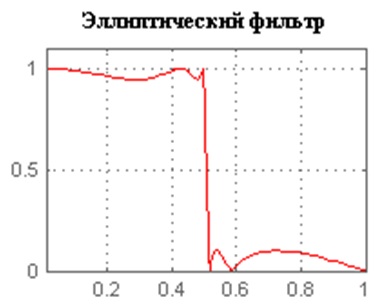
Эллиптический фильтр (Фильтр Кауэра) — электронный фильтр, характерной особенностью которого являются пульсации амплитудно-частотной характеристики как в полосе пропускания, так и полосе подавления. С помощью этого фильтра можно достигать более эффективного разделения частот, чем с помощью других линейных фильтров.

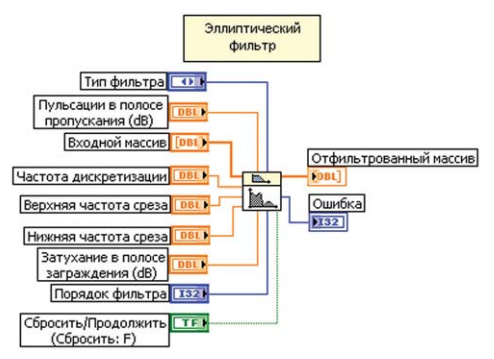
Рис.19 Эллиптический фильтр (Elliptic) с выходами

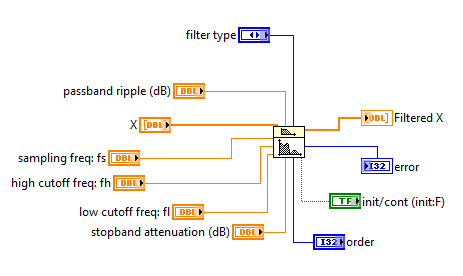
Рис.20 Эллиптический фильтр (Elliptic) с выходами

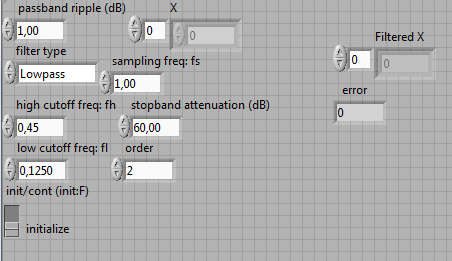
Рис. 21 Панель управления эллиптического фильтра (Elliptic)